60 Of 21
interactiveleap
Sep 14, 2025 · 5 min read
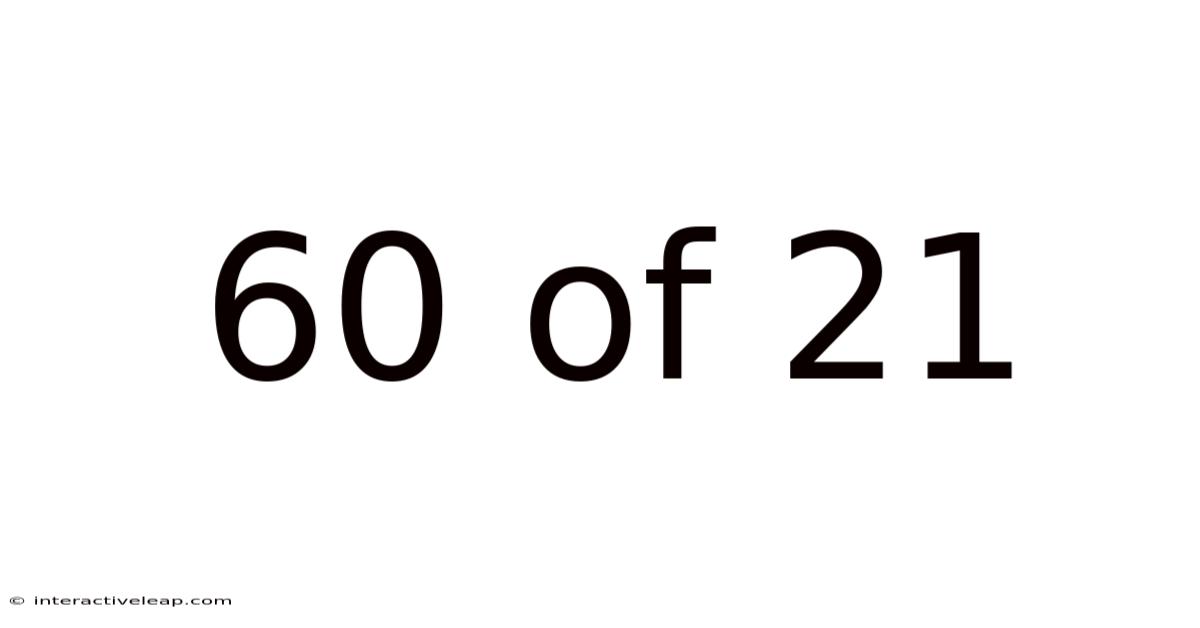
Table of Contents
Decoding the Enigma: Understanding 60/21 and its Applications
The seemingly simple fraction 60/21 might appear insignificant at first glance. However, a deeper dive reveals a rich mathematical landscape with applications extending beyond basic arithmetic. This article will explore the multifaceted nature of 60/21, examining its simplification, decimal representation, applications in various fields, and addressing common misconceptions. We'll delve into its mathematical properties and uncover its hidden potential, demonstrating its relevance in diverse contexts. By the end, you'll appreciate the surprising depth and utility concealed within this seemingly ordinary fraction.
I. Simplification and Core Properties
The fraction 60/21, at its core, represents the ratio of 60 to 21. The immediate task is to simplify it to its lowest terms. Both the numerator (60) and the denominator (21) share a common factor of 3. Dividing both by 3, we get:
60 ÷ 3 = 20 21 ÷ 3 = 7
Therefore, the simplified form of 60/21 is 20/7. This simplified fraction is irreducible, meaning no further common factors exist between the numerator and the denominator. This simplified form is crucial for various calculations and comparisons.
II. Decimal Representation and Approximations
Converting the fraction 20/7 into a decimal representation reveals a recurring decimal. Performing the long division, we find:
20 ÷ 7 ≈ 2.857142857142...
The sequence "857142" repeats infinitely. This recurring decimal nature is important when dealing with applications requiring precise numerical values. In situations where perfect accuracy isn't essential, approximations can be used. For example, 2.86 or 2.9 could serve as reasonable approximations depending on the level of precision required. Understanding the degree of error introduced by such approximations is vital for accurate application in fields like engineering and finance.
III. Applications Across Disciplines
While seemingly a simple fraction, 60/21 (or its simplified form 20/7) finds applications in diverse fields. Let's explore a few examples:
-
Engineering and Physics: Ratios and proportions are fundamental to engineering and physics. The fraction could represent a gear ratio in a mechanical system, the ratio of forces acting on an object, or even a scaling factor in a design. Understanding its decimal representation and potential for approximation is crucial for making accurate calculations.
-
Finance and Economics: In finance, ratios are used extensively for analyzing financial statements. The fraction could represent a profit margin, a debt-to-equity ratio, or a return on investment. The accuracy of calculations involving such ratios directly impacts financial decisions. Understanding the implications of rounding or approximation is critical.
-
Computer Science: In computer graphics and image processing, fractions are often used to represent scaling factors or coordinate transformations. The fraction's decimal representation, especially its recurring nature, needs careful handling to avoid accumulating rounding errors that can distort the image or calculation results.
-
Everyday Life: Even in everyday life, the concept of ratios is present. For example, if a recipe calls for 20 parts of one ingredient to 7 parts of another, the ratio is 20/7. The ability to understand and work with this ratio is crucial for accurate baking or cooking.
-
Mathematics itself: The fraction 20/7 serves as a great example in teaching concepts such as simplification, decimal representation, recurring decimals, and the importance of understanding approximations and their limitations. It's a simple yet powerful tool for exploring fundamental mathematical principles.
IV. Advanced Mathematical Considerations
Beyond its practical applications, 60/21 offers opportunities for exploring advanced mathematical concepts. Here are a few:
-
Continued Fractions: The fraction 20/7 can be expressed as a continued fraction, offering an alternative representation and enabling deeper mathematical analysis. This representation provides insights into the fraction's properties and its relationship to other mathematical concepts.
-
Approximation Theory: The recurring decimal nature of 20/7 provides an excellent case study for exploring approximation theory. Investigating different methods of approximation, such as truncation or rounding, and analyzing the resulting errors, highlights the complexities and nuances of approximating irrational numbers.
-
Number Theory: The fraction's properties can be analyzed using concepts from number theory, examining its relationship to prime numbers, divisors, and other relevant concepts. This can lead to deeper insights into the structure and behavior of rational numbers.
V. Addressing Common Misconceptions
There are a few common misconceptions surrounding fractions like 60/21:
-
Incorrect Simplification: A common mistake is failing to simplify the fraction completely, leading to inaccurate calculations and analysis. Always ensure you simplify the fraction to its lowest terms before proceeding with any further calculations.
-
Misunderstanding Recurring Decimals: The infinite repeating decimal nature of 20/7 might be confusing. It's essential to understand that this is a characteristic of many rational numbers, and proper techniques are required to handle them in calculations.
-
Overreliance on Approximations: While approximations are useful in many contexts, it's crucial to understand the limitations and potential errors introduced by using approximate values. Always assess the impact of approximation on the overall result.
VI. Practical Exercises and Further Exploration
To solidify your understanding of 60/21 and related concepts, consider these exercises:
-
Simplification Practice: Simplify the following fractions: 90/35, 120/42, 150/63. Compare your results and explain the process.
-
Decimal Conversion: Convert the simplified fractions from Exercise 1 into their decimal representations. Identify which are recurring decimals and describe the repeating pattern.
-
Approximation Analysis: Approximate the decimal representations from Exercise 2 to two decimal places. Calculate the error introduced by the approximation in each case.
-
Real-World Application: Think of a real-world scenario where the ratio 20/7 might be relevant. Describe the scenario and how the ratio is applied.
VII. Conclusion: The Significance of Simplicity
The fraction 60/21, though seemingly simple, serves as a powerful demonstration of the interconnectedness of various mathematical concepts. From its basic simplification to its advanced applications in diverse fields, this seemingly ordinary fraction unveils a wealth of knowledge and opportunity for deeper exploration. Understanding its properties, its decimal representation, and the potential for error in approximation is crucial for accurate calculations and insightful analysis across numerous disciplines. The journey from 60/21 to its simplified form 20/7, and further into its decimal representation and applications, underscores the importance of appreciating the depth and significance hidden within even the most seemingly basic mathematical constructs. By mastering the principles illustrated through this single fraction, we lay a solid foundation for tackling more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
4 X X2
Sep 14, 2025
-
Information Data Difference
Sep 14, 2025
-
3c To Fahrenheit
Sep 14, 2025
-
Kj In Kw
Sep 14, 2025
-
7 5 In Centimeters
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.