4 X X2
interactiveleap
Sep 14, 2025 · 6 min read
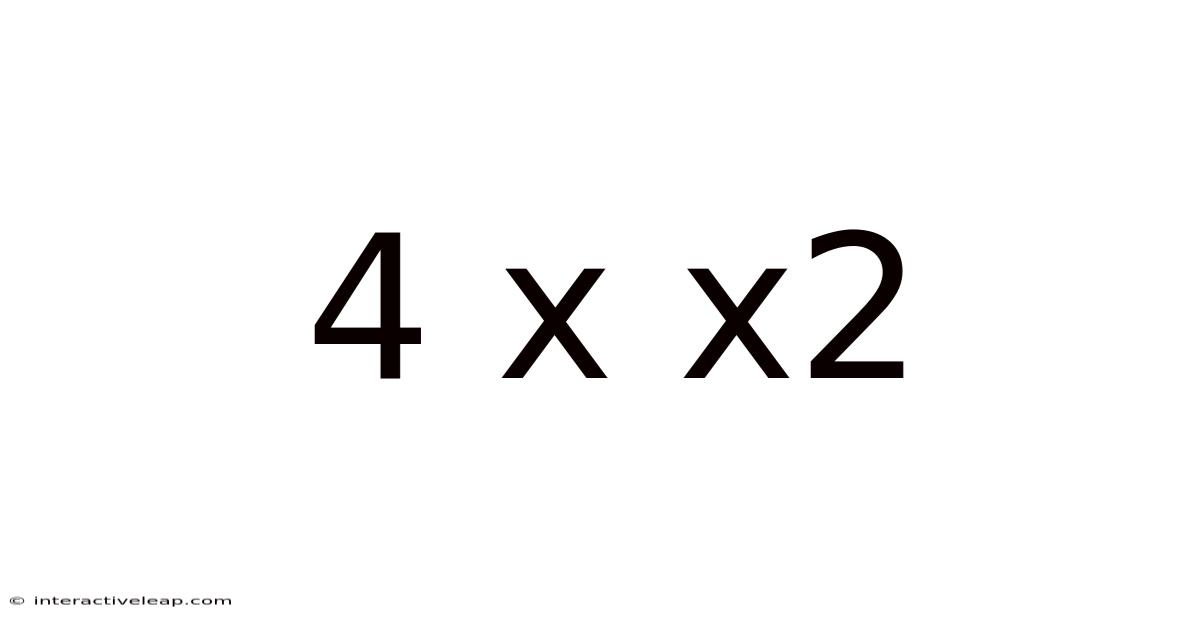
Table of Contents
Decoding 4 x x²: Unveiling the Mysteries of Quadratic Expressions
This article delves into the intricacies of the mathematical expression "4 x x²," exploring its simplification, applications, and broader implications within the realm of algebra and beyond. We will unpack the fundamental concepts, offer step-by-step explanations, and address frequently asked questions to provide a comprehensive understanding suitable for students and enthusiasts alike. Understanding this seemingly simple expression opens doors to a deeper appreciation of quadratic equations and their pervasive role in various fields.
Understanding the Fundamentals: Variables and Exponents
Before diving into the specifics of "4 x x²," let's establish a solid foundation. The expression involves two core components: variables and exponents.
-
Variables: In mathematics, a variable is a symbol (typically a letter like x, y, or z) representing an unknown quantity or a quantity that can change. In our expression, 'x' is the variable.
-
Exponents: Exponents (also called powers or indices) indicate repeated multiplication. For example, x² (pronounced "x squared") means x * x. The small '2' is the exponent, showing that 'x' is multiplied by itself.
Simplifying the Expression: Combining Like Terms
The expression "4 x x²" contains like terms that can be simplified. Remember the rule of exponents: when multiplying terms with the same base (in this case, 'x'), we add the exponents. Since x can be written as x¹, our expression becomes:
4 * x¹ * x²
Adding the exponents (1 + 2 = 3), we arrive at the simplified expression:
4x³
This means "4 times x cubed," or four times x multiplied by itself three times (x * x * x). This simplified form is crucial for further calculations and problem-solving.
Applications of 4x³: Real-World Examples
The expression 4x³ and its broader family of cubic equations have widespread applications in various fields. Let's explore a few examples:
-
Volume Calculations: Imagine a cube with side length 'x'. The volume of a cube is calculated as side * side * side, or x³. If we have four such cubes, the total volume would be 4x³. This is a simple yet fundamental application in geometry.
-
Physics and Engineering: Cubic equations frequently appear in physics and engineering problems related to:
- Fluid dynamics: Modeling fluid flow and pressure.
- Projectile motion: Calculating the trajectory of objects.
- Structural analysis: Determining stress and strain on structures.
- Electrical circuits: Analyzing current and voltage relationships.
-
Economics and Finance: Cubic functions can model various economic phenomena, such as:
- Cost functions: Representing the total cost of producing a certain quantity of goods.
- Revenue functions: Modeling the total revenue generated from sales.
- Growth models: Describing the growth of investments or populations.
-
Computer Science: Cubic equations play a role in:
- Algorithm design: Developing efficient algorithms for various tasks.
- Computer graphics: Creating smooth curves and 3D models.
- Data analysis: Fitting curves to data sets.
These applications highlight the practical significance of understanding and manipulating expressions like 4x³. The ability to simplify and solve equations involving cubic terms is essential in numerous real-world scenarios.
Exploring Further: Quadratic Equations and Their Relationship
While our initial focus was on the cubic expression 4x³, it’s important to understand its relationship to quadratic equations. Although 4x³ is not a quadratic (quadratic equations have a highest power of 2), the process of simplifying it uses foundational algebraic principles that are critical for working with quadratics.
Quadratic equations are of the form ax² + bx + c = 0, where a, b, and c are constants and a ≠ 0. These equations have a wide range of applications, particularly in:
- Projectile motion: Calculating the height of a projectile at a given time.
- Area calculations: Determining the area of geometric shapes.
- Optimization problems: Finding maximum or minimum values of functions.
Understanding how to simplify expressions involving variables and exponents, as demonstrated with 4x x², is a crucial prerequisite for solving quadratic equations and tackling more complex mathematical problems.
Expanding the Concept: Polynomials and Their Properties
The expression 4x³ falls under the broader category of polynomials. A polynomial is an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. 4x³ is a monomial (a polynomial with only one term), while expressions like 2x² + 3x - 5 are polynomials with multiple terms.
Studying polynomials involves understanding their:
- Degree: The highest power of the variable (in 4x³, the degree is 3).
- Coefficients: The numerical factors of the terms (in 4x³, the coefficient is 4).
- Roots or zeros: The values of the variable that make the polynomial equal to zero.
Understanding the properties of polynomials provides a framework for solving more complex equations and inequalities.
Solving Equations Involving 4x³: A Step-by-Step Guide
Let's consider a simple equation involving our simplified expression:
4x³ = 64
To solve for 'x', we follow these steps:
-
Isolate the variable term: Divide both sides of the equation by 4: x³ = 16
-
Find the cube root: Take the cube root of both sides to isolate 'x': x = ³√16
While the cube root of 16 isn't a whole number, we can approximate it or express it using radicals. This demonstrates a fundamental process in solving polynomial equations. More complex equations might require more sophisticated methods like factoring or using the quadratic formula (although not directly applicable here because it's a cubic).
Frequently Asked Questions (FAQ)
Q1: Can I simplify 4x x² in a different way?
A1: While the method presented is the most efficient, you could expand the expression first: 4 * x * x * x, which leads to the same simplified form: 4x³.
Q2: What if the expression was 4x² x²?
A2: In this case, you'd add the exponents of the x terms: 4 * x⁽²⁺²⁾ = 4x⁴. This demonstrates the flexibility of exponent rules in simplifying various expressions.
Q3: What is the difference between a quadratic and a cubic equation?
A3: A quadratic equation has a highest power of 2 (e.g., ax² + bx + c = 0), while a cubic equation has a highest power of 3 (e.g., ax³ + bx² + cx + d = 0). They differ in their degree and, consequently, the number of potential solutions.
Q4: How do I solve more complex equations involving 4x³?
A4: Solving more complex equations might involve techniques like factoring, using the rational root theorem, or numerical methods (like the Newton-Raphson method). These advanced techniques are typically covered in higher-level algebra courses.
Conclusion: Mastering the Fundamentals for Future Success
The seemingly simple expression "4 x x²" serves as a gateway to a deeper understanding of algebra, polynomials, and their diverse applications. Through simplification, we uncovered the underlying principles of exponents and variables. We explored its real-world relevance in fields ranging from geometry to engineering. By understanding the fundamentals illustrated here, you're building a solid base for tackling more complex mathematical problems and applying these concepts to real-world situations. The journey of mathematical exploration is ongoing, and mastering these basic building blocks is essential for continued growth and success in this fascinating field.
Latest Posts
Latest Posts
-
25 Of 19
Sep 14, 2025
-
Duchess Of Newcastle
Sep 14, 2025
-
Milligram To Kg
Sep 14, 2025
-
0 03 As Fraction
Sep 14, 2025
-
Highest Note Song
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 4 X X2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.