6/5 X 6/5
interactiveleap
Sep 20, 2025 · 5 min read
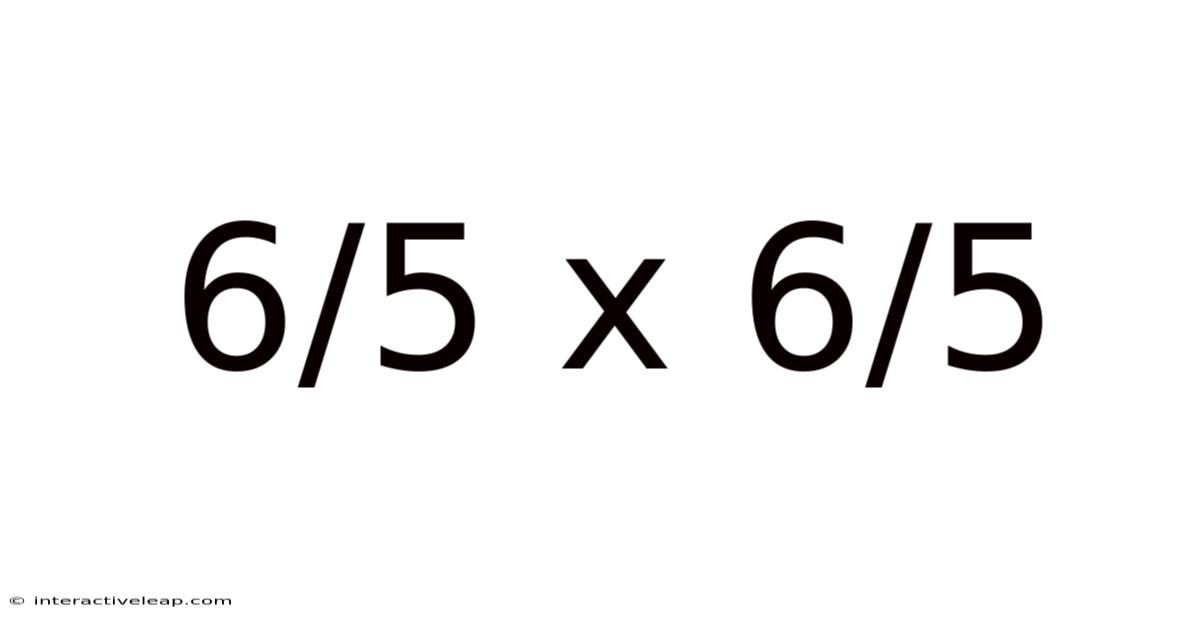
Table of Contents
Unveiling the Mysteries of 6/5 x 6/5: A Deep Dive into Fraction Multiplication
This article explores the seemingly simple calculation of 6/5 x 6/5, delving far beyond the immediate answer to uncover the underlying principles of fraction multiplication, its practical applications, and its relevance in various mathematical contexts. We'll dissect the process step-by-step, explore related concepts, and address frequently asked questions, ensuring a comprehensive understanding for learners of all levels. Understanding fraction multiplication is fundamental to grasping more advanced mathematical concepts, making this exploration crucial for your mathematical journey.
Understanding Fractions: A Quick Refresher
Before diving into the multiplication, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 6/5, 6 is the numerator and 5 is the denominator. This means we're dealing with 6 parts of a whole that has been divided into 5 equal parts. Note that 6/5 is an improper fraction because the numerator is larger than the denominator, signifying a value greater than 1.
Multiplying Fractions: The Simple Process
Multiplying fractions is remarkably straightforward. The process involves two simple steps:
- Multiply the numerators: Multiply the top numbers of both fractions together.
- Multiply the denominators: Multiply the bottom numbers of both fractions together.
The resulting fraction is the product of the two original fractions. Let's apply this to our problem: 6/5 x 6/5.
- Step 1: Multiply the numerators: 6 x 6 = 36
- Step 2: Multiply the denominators: 5 x 5 = 25
Therefore, 6/5 x 6/5 = 36/25.
Interpreting the Result: Improper Fractions and Mixed Numbers
Our answer, 36/25, is an improper fraction. While mathematically correct, it's often more practical to express it as a mixed number. A mixed number combines a whole number and a proper fraction. To convert 36/25 to a mixed number, we perform a division:
36 ÷ 25 = 1 with a remainder of 11.
This means 36/25 can be expressed as 1 11/25. This tells us that 6/5 multiplied by itself is equal to one whole and eleven twenty-fifths.
Visualizing Fraction Multiplication: A Geometric Approach
Visualizing fraction multiplication can enhance understanding. Imagine a square representing 'one whole'. Dividing this square into 5 equal columns and 5 equal rows creates 25 smaller squares (5 x 5 = 25). Each smaller square represents 1/25 of the whole. Now, if we consider 6/5, we are dealing with 6 parts out of the 5 parts created by the initial division. This visually demonstrates how the result becomes an improper fraction. The calculation of 6/5 x 6/5 represents taking 6/5 of this section, which results in the 36/25, representing more than one whole square.
Practical Applications of Fraction Multiplication
Fraction multiplication isn't just an abstract mathematical exercise; it has numerous real-world applications:
- Cooking and Baking: Scaling recipes up or down requires fraction multiplication. If a recipe calls for 2/3 cup of flour and you want to double it, you'd calculate 2/3 x 2.
- Construction and Engineering: Calculating material quantities, determining precise measurements, and understanding scale models often involve fraction multiplication.
- Finance: Calculating percentages, interest rates, and proportional shares of investments frequently utilize fraction multiplication.
- Data Analysis: Many statistical calculations rely on understanding and manipulating fractions.
Beyond the Basics: Expanding on Fraction Multiplication
Understanding 6/5 x 6/5 provides a foundation for exploring more complex fractional calculations:
- Multiplying More Than Two Fractions: The same principle extends to multiplying three or more fractions; simply multiply all numerators together and all denominators together.
- Multiplying Mixed Numbers: To multiply mixed numbers, convert them to improper fractions first, then proceed with the standard multiplication process.
- Simplifying Fractions: Before or after multiplication, it's often beneficial to simplify fractions by finding common factors in the numerator and denominator. This makes the calculations easier and presents the answer in its simplest form. For example, 36/25 is already in its simplest form because 36 and 25 share no common factors other than 1.
The Significance of Improper Fractions
Improper fractions, like the 36/25 we obtained, are an essential part of mathematics. They represent values greater than one, providing a more direct and efficient way to represent quantities compared to constantly working with mixed numbers, especially when performing further calculations.
Addressing Common Questions (FAQ)
Q: Why is multiplying fractions different from adding or subtracting them?
A: Adding and subtracting fractions require a common denominator – the bottom numbers must be the same. Multiplying fractions doesn't need a common denominator; you simply multiply the numerators and denominators directly.
Q: What if one of the fractions is a whole number?
A: Express the whole number as a fraction with a denominator of 1 (e.g., 3 becomes 3/1). Then, apply the standard fraction multiplication process.
Q: How do I convert an improper fraction to a decimal?
A: Divide the numerator by the denominator. For example, 36/25 = 1.44
Q: Are there any online tools or calculators to help with fraction multiplication?
A: Many online calculators are available to assist with fraction calculations. These can be particularly helpful for complex problems or to verify your manual calculations. However, it’s vital to understand the underlying process to apply it effectively in different situations.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication, even a seemingly simple calculation like 6/5 x 6/5, is a cornerstone of mathematical proficiency. This article has explored the mechanics of the process, its practical applications, and the importance of understanding improper fractions and mixed numbers. By understanding the principles behind this calculation, you're building a strong foundation for more advanced mathematical concepts and problem-solving. Remember that practice is key – the more you work with fractions, the more confident and fluent you'll become. So, grab a pencil and paper, work through some examples, and continue to build your mathematical skills! This comprehensive understanding will serve you well throughout your mathematical journey and in numerous real-world situations. Don't hesitate to revisit these concepts and explore further resources as you delve deeper into the fascinating world of mathematics.
Latest Posts
Latest Posts
-
My Daughter French
Sep 20, 2025
-
1 1 2 Tbsp
Sep 20, 2025
-
23 X 7
Sep 20, 2025
-
10 Of 800 00
Sep 20, 2025
-
212f To C
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 6/5 X 6/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.