6 20 Simplified
interactiveleap
Sep 23, 2025 · 5 min read
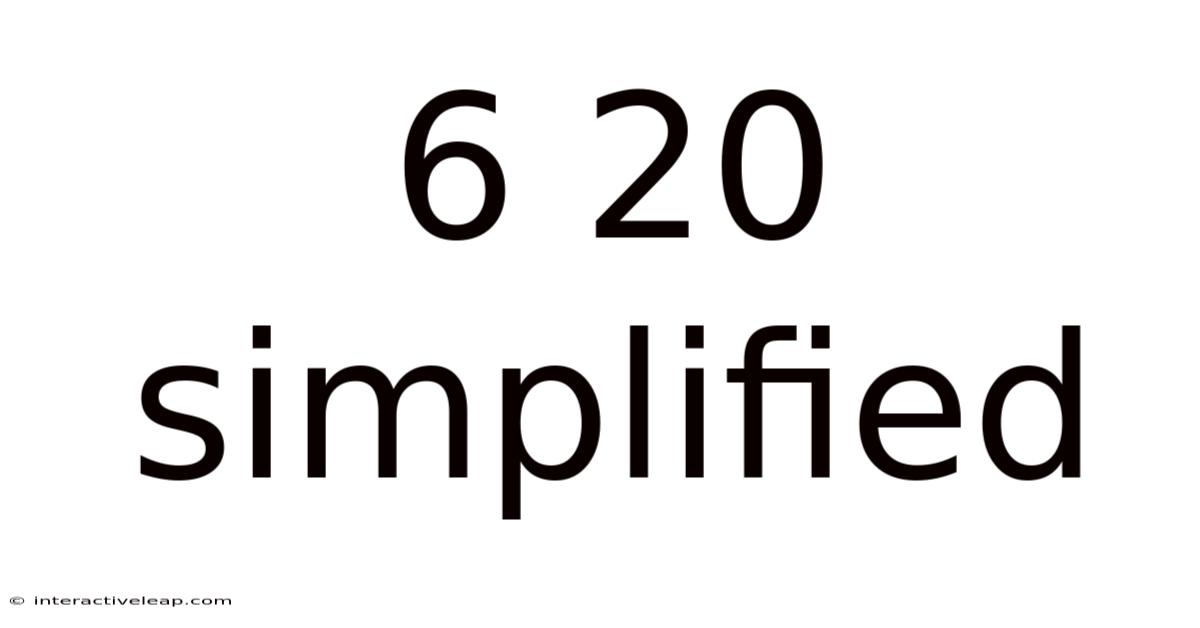
Table of Contents
Understanding 6/20 Simplified: A Comprehensive Guide
Introduction:
The fraction 6/20, or six twentieths, is a common example used in elementary math to teach simplification of fractions. Understanding how to simplify fractions is crucial for further mathematical learning, as it lays the foundation for working with ratios, proportions, and more complex algebraic concepts. This guide will thoroughly explain the process of simplifying 6/20, providing a step-by-step approach, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll also delve into the broader concept of fraction simplification and its real-world applications.
Understanding Fractions:
Before diving into simplifying 6/20, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a line. The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 6/20, 6 is the numerator and 20 is the denominator. This means we have 6 parts out of a total of 20 equal parts.
Simplifying Fractions: The Concept
Simplifying a fraction means expressing it in its lowest terms. This means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. Simplifying doesn't change the value of the fraction; it just makes it easier to understand and work with. Think of it like reducing a recipe – you can halve or quarter the ingredients, and the result will still taste the same.
Step-by-Step Simplification of 6/20:
The key to simplifying fractions lies in finding the greatest common divisor (GCD), also known as the greatest common factor (GCF), of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
-
Find the factors of the numerator (6): The factors of 6 are 1, 2, 3, and 6.
-
Find the factors of the denominator (20): The factors of 20 are 1, 2, 4, 5, 10, and 20.
-
Identify the greatest common factor (GCF): By comparing the lists of factors, we see that the largest number that appears in both lists is 2. Therefore, the GCF of 6 and 20 is 2.
-
Divide both the numerator and the denominator by the GCF: Divide 6 by 2 and 20 by 2:
6 ÷ 2 = 3 20 ÷ 2 = 10
-
The simplified fraction: The simplified fraction of 6/20 is 3/10.
Therefore, 6/20 is equivalent to 3/10. Both fractions represent the same proportion or quantity.
Alternative Method: Prime Factorization
Another method to find the GCF involves prime factorization. Prime factorization is expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
-
Prime factorization of 6: 6 = 2 x 3
-
Prime factorization of 20: 20 = 2 x 2 x 5 = 2² x 5
-
Identifying common factors: We see that both 6 and 20 share one factor of 2.
-
Simplifying: Divide both the numerator and denominator by the common factor (2):
(2 x 3) ÷ 2 = 3 (2² x 5) ÷ 2 = 2 x 5 = 10
This again results in the simplified fraction 3/10.
Visual Representation:
Imagine a pizza cut into 20 equal slices. 6/20 represents having 6 slices of that pizza. If we group the slices into pairs (2 slices per group), we have 3 groups out of a total of 10 groups. This visually demonstrates the equivalence of 6/20 and 3/10.
Real-World Applications of Fraction Simplification:
Simplifying fractions is not just an abstract mathematical exercise. It has numerous real-world applications:
- Cooking and Baking: Recipes often use fractions. Simplifying fractions allows for easier measurement and scaling of ingredients.
- Construction and Engineering: Precise measurements are critical in construction and engineering. Simplifying fractions ensures accurate calculations and efficient resource allocation.
- Finance: Understanding fractions is essential for managing budgets, calculating interest rates, and comprehending financial reports.
- Data Analysis: In statistical analysis and data interpretation, simplified fractions often provide a clearer representation of proportions and percentages.
Further Exploration: Working with More Complex Fractions
While 6/20 is a relatively simple fraction to simplify, the same principles apply to more complex fractions. The key is always to find the greatest common factor of the numerator and denominator and divide both by that factor. If you encounter a fraction where the GCF isn't immediately apparent, you can use prime factorization to systematically find it.
Frequently Asked Questions (FAQ):
-
Q: What if the numerator and denominator have no common factors other than 1?
- A: If the GCF is 1, the fraction is already in its simplest form. It cannot be simplified further.
-
Q: Can I simplify a fraction by dividing the numerator and denominator by different numbers?
- A: No. You must divide both the numerator and denominator by the same number to maintain the equivalence of the fraction. Dividing by different numbers will change the value of the fraction.
-
Q: Is there a quick way to simplify fractions?
- A: For simple fractions, you might be able to spot the GCF quickly. For more complex fractions, prime factorization is a reliable method. Practice will help you develop intuition and speed.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also leads to more efficient problem-solving.
-
Q: What happens if I simplify a fraction incorrectly?
- A: An incorrect simplification will result in an equivalent fraction that is not in its lowest terms. This can lead to errors in further calculations or interpretations.
Conclusion:
Simplifying fractions, as demonstrated with the example of 6/20, is a fundamental skill in mathematics. Mastering this skill opens doors to a deeper understanding of more complex mathematical concepts and their real-world applications. By understanding the underlying principles and using the steps outlined above, you can confidently simplify any fraction and apply this valuable skill to various aspects of life. Remember, practice is key – the more you work with fractions, the more comfortable and proficient you will become. Don't hesitate to revisit this guide and use different methods to reinforce your understanding. The goal is not just to get the right answer, but to truly grasp the concept of simplification and its importance in the broader world of mathematics.
Latest Posts
Latest Posts
-
7 5 X 7
Sep 23, 2025
-
Round Crossword Clue
Sep 23, 2025
-
3 3km Into Miles
Sep 23, 2025
-
3800m In Miles
Sep 23, 2025
-
Lutheran Vs Catholicism
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 6 20 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.