7/5 X 7
interactiveleap
Sep 23, 2025 · 6 min read
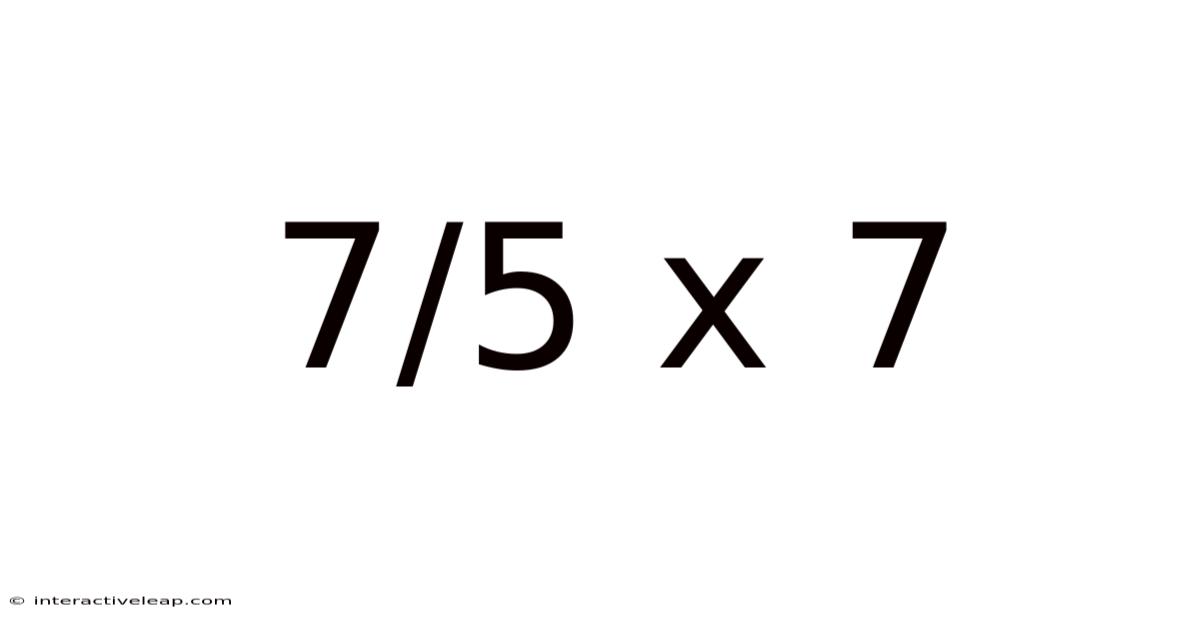
Table of Contents
Unpacking 7/5 x 7: A Deep Dive into Fraction Multiplication
This article explores the seemingly simple calculation of 7/5 x 7, delving beyond the immediate answer to understand the underlying principles of fraction multiplication, its practical applications, and how to approach similar problems with confidence. We'll cover the mechanics, the reasoning, and explore some related concepts to provide a comprehensive understanding of this fundamental mathematical operation. Understanding fraction multiplication is crucial for various fields, from baking and cooking to engineering and finance.
Understanding Fractions: A Quick Refresher
Before tackling 7/5 x 7, let's briefly review the basics of fractions. A fraction represents a part of a whole. It's written as a numerator (the top number) over a denominator (the bottom number), separated by a horizontal line. The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 7/5, 7 is the numerator and 5 is the denominator. This means we have 7 parts of a whole that's divided into 5 equal parts. Note that 7/5 is an improper fraction because the numerator is larger than the denominator, indicating a value greater than 1.
Calculating 7/5 x 7: Step-by-Step
Now, let's address the core calculation: 7/5 x 7. Multiplying a fraction by a whole number is straightforward. We can think of the whole number, 7, as a fraction itself: 7/1. This doesn't change its value, as any number divided by 1 remains the same. Therefore, our problem becomes:
(7/5) x (7/1)
The process involves multiplying the numerators together and the denominators together separately:
- Numerator multiplication: 7 x 7 = 49
- Denominator multiplication: 5 x 1 = 5
This gives us the result: 49/5
This is still an improper fraction. To express this as a mixed number (a whole number and a fraction), we perform division:
49 ÷ 5 = 9 with a remainder of 4
Therefore, 49/5 can be written as 9 4/5. This means that 7/5 multiplied by 7 equals 9 and 4/5.
Visualizing the Multiplication
Let's visualize this using a real-world example. Imagine you have 7 pizzas, each cut into 5 equal slices (representing the fraction 7/5). If you want to take 7 slices from each pizza, you would be taking 7 x 7 = 49 slices in total. Since each pizza has 5 slices, you've taken 49/5 pizzas worth of slices. That's equivalent to 9 whole pizzas and 4/5 of another pizza.
The Commutative Property and Fraction Multiplication
The commutative property of multiplication states that the order of the factors doesn't change the product. In our case:
7/5 x 7 = 7 x 7/5
This means we can multiply the whole number by the numerator first: 7 x 7 = 49, and then keep the denominator as it is: 49/5. This leads to the same result, demonstrating the flexibility of the commutative property in fraction multiplication.
Extending the Understanding: Multiplying Fractions with Different Denominators
While our example focused on multiplying a fraction by a whole number, the principles extend to multiplying two fractions with different denominators. For instance, consider 2/3 x 5/7:
- Numerator multiplication: 2 x 5 = 10
- Denominator multiplication: 3 x 7 = 21
The result is 10/21. This simple process highlights the core concept: Multiply the numerators, multiply the denominators.
Simplifying Fractions: A Crucial Step
Sometimes, after multiplying fractions, the resulting fraction can be simplified. Simplifying means reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For example, if we had the result 12/18, the GCD of 12 and 18 is 6. Dividing both numerator and denominator by 6 gives us 2/3, which is the simplified form. In our initial calculation (49/5), the fraction is already in its simplest form because 49 and 5 share no common factors other than 1.
Practical Applications of Fraction Multiplication
Fraction multiplication isn't just a theoretical exercise; it's essential in various real-world scenarios:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Multiplying fractions is necessary when scaling up or down a recipe. For example, if a recipe calls for 1/2 cup of sugar, and you want to double the recipe, you'll need to calculate 2 x (1/2) = 1 cup of sugar.
-
Construction and Engineering: Precise measurements are vital, and fractions are frequently used. Calculating areas, volumes, and material quantities involves multiplying fractions.
-
Finance: Understanding percentages and proportions, often expressed as fractions, is fundamental to various financial calculations, including interest calculations, profit margins, and budgeting.
-
Data Analysis: In statistics and data analysis, handling proportions and probabilities often involves multiplication of fractions.
Frequently Asked Questions (FAQ)
Q: Why do we multiply numerators and denominators separately?
A: The fundamental reason is that we're essentially multiplying parts of wholes. Multiplying the numerators gives us the total number of parts we have, while multiplying the denominators gives us the total number of parts the whole is divided into.
Q: What if I have more than two fractions to multiply?
A: The process remains the same. Multiply all the numerators together, and then multiply all the denominators together. For example: (1/2) x (3/4) x (5/6) = (1 x 3 x 5) / (2 x 4 x 6) = 15/48. This can be simplified to 5/16.
Q: Is there a way to estimate the result before calculating?
A: Yes, you can get a rough estimate by rounding the fractions to the nearest whole number or a simpler fraction. For example, in 7/5 x 7, 7/5 is approximately 1.5, so 1.5 x 7 is approximately 10.5. This gives you a general idea of the magnitude of the answer.
Q: What if one of the numbers is a negative fraction?
A: Multiply the numbers as usual, remembering the rules for multiplying signed numbers. If you multiply a positive fraction by a negative fraction, the result will be negative. If you multiply two negative fractions, the result will be positive.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a cornerstone of mathematical understanding. While the core concept is simple—multiply numerators, multiply denominators—a deeper understanding of the underlying principles, its applications, and the ability to simplify fractions leads to greater confidence and proficiency in tackling more complex mathematical challenges. This article aimed not just to explain the calculation of 7/5 x 7 but to build a strong foundation for understanding fractional arithmetic, empowering you to confidently approach similar problems and apply this knowledge to various real-world situations. Remember to practice regularly and visualize the process; this will solidify your grasp of these fundamental mathematical concepts.
Latest Posts
Latest Posts
-
Stock Control Systems
Sep 23, 2025
-
Gigantic Or Colossal
Sep 23, 2025
-
128 64 32
Sep 23, 2025
-
120kg In Lb
Sep 23, 2025
-
6 Times 40
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 7/5 X 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.