56 X 7
interactiveleap
Sep 22, 2025 · 6 min read
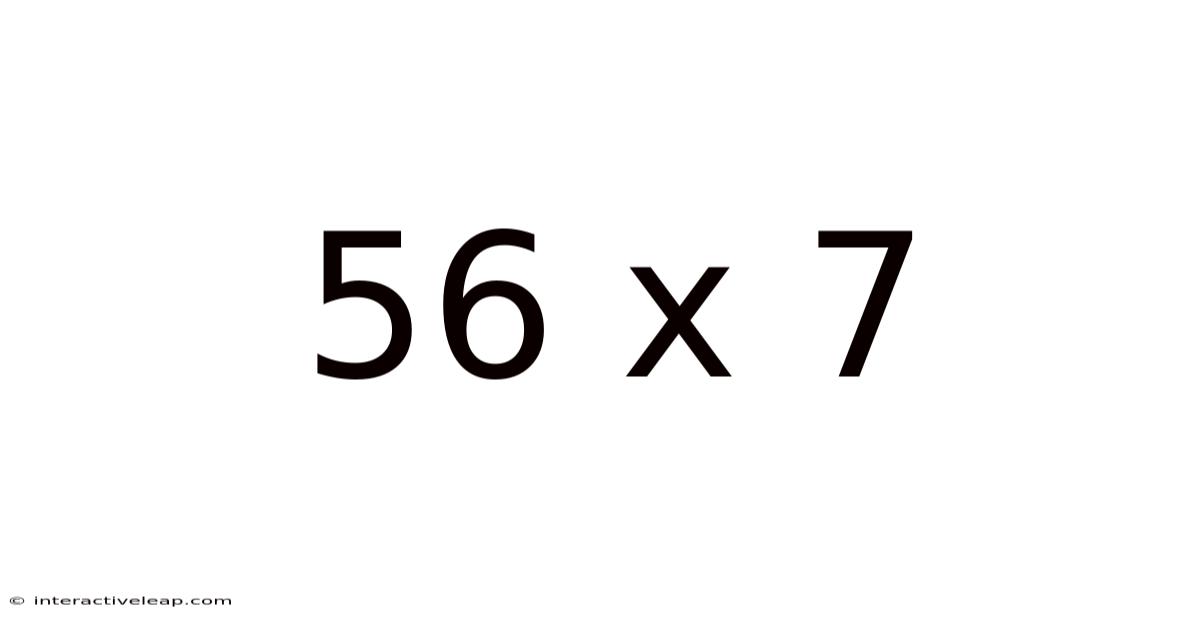
Table of Contents
Unlocking the Secrets of 56 x 7: A Deep Dive into Multiplication
This article explores the seemingly simple multiplication problem, 56 x 7, transforming it from a basic arithmetic exercise into a gateway to understanding fundamental mathematical concepts. We will delve into various methods for solving this problem, examining the underlying principles of multiplication and exploring its applications in real-world scenarios. Whether you're a student brushing up on your multiplication tables, a teacher looking for engaging teaching strategies, or simply someone curious about the beauty of mathematics, this comprehensive guide will provide valuable insights.
Introduction: More Than Just a Number
At first glance, 56 x 7 appears straightforward. However, understanding the intricacies of this seemingly simple calculation opens doors to a deeper appreciation of mathematics. This problem isn't just about finding the answer; it's about grasping the fundamental concepts of multiplication, exploring different solution methods, and appreciating the practical applications of this core mathematical operation. We’ll dissect this problem, exploring its solution through various methods, including traditional multiplication, the distributive property, and mental math techniques. We’ll also discuss the historical context of multiplication and its relevance in various fields.
Method 1: Traditional Multiplication
The most common approach to solving 56 x 7 is through traditional long multiplication. This method involves breaking down the multiplication into smaller, manageable steps:
-
Multiply the ones digit: 7 x 6 = 42. Write down the '2' and carry-over the '4'.
-
Multiply the tens digit: 7 x 5 = 35. Add the carry-over '4': 35 + 4 = 39.
-
Combine the results: The final answer is 392.
Therefore, 56 x 7 = 392. This method is foundational and helps build a strong understanding of place value and the distributive property, which we’ll explore further.
Method 2: The Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can apply this to solve 56 x 7 by breaking down 56 into smaller, easier-to-manage numbers:
56 can be broken down as 50 + 6. Therefore, 56 x 7 can be rewritten as (50 + 6) x 7.
Applying the distributive property:
(50 + 6) x 7 = (50 x 7) + (6 x 7) = 350 + 42 = 392
This method demonstrates a deeper understanding of the mathematical principles behind multiplication. It shows how multiplication can be broken down into simpler calculations, making it easier to solve, especially for larger numbers. This technique is crucial for building mental math skills.
Method 3: Mental Math Techniques
With practice, solving 56 x 7 mentally becomes achievable. Here are a few techniques:
-
Breaking it down: As demonstrated with the distributive property, breaking down 56 into 50 and 6 simplifies the calculation.
-
Rounding and adjusting: Round 56 to 60. 60 x 7 = 420. Since we rounded up by 4, subtract 4 x 7 = 28 from 420: 420 - 28 = 392.
-
Doubling and halving: Double 7 to 14. Halve 56 to 28. Now multiply 28 x 14. This might seem more complex initially, but with practice, it becomes efficient for certain numbers.
Understanding Place Value: The Foundation of Multiplication
The success of any multiplication method hinges on a strong understanding of place value. In the number 56, the '5' represents 5 tens (50) and the '6' represents 6 ones. When we multiply 56 by 7, we are essentially multiplying both the tens and ones place values separately and then adding the results. This highlights the importance of place value in arithmetic operations.
The Historical Context of Multiplication
Multiplication, as a mathematical concept, has evolved over centuries. Ancient civilizations used various methods, often relying on visual aids and practical applications like counting objects or measuring land. The development of efficient algorithms, like the long multiplication method we discussed, significantly improved calculation speed and accuracy. Understanding the historical development of multiplication provides context and appreciation for the mathematical systems we use today.
Applications of Multiplication: Real-World Scenarios
Multiplication isn't confined to textbooks; it's a crucial tool in numerous real-world applications:
-
Shopping: Calculating the total cost of multiple items. For example, if each item costs $56 and you buy 7, the total cost is 56 x 7 = $392.
-
Construction: Determining the amount of material needed for a project. If a project requires 56 units of material per section and you have 7 sections, the total requirement is 56 x 7 = 392 units.
-
Cooking: Scaling up or down recipes. If a recipe calls for 56 grams of flour and you want to make 7 times the recipe, you’ll need 56 x 7 = 392 grams of flour.
-
Finance: Calculating interest or earnings. Numerous financial calculations rely heavily on multiplication.
-
Data Analysis: In fields like statistics and data science, multiplication plays a crucial role in many calculations.
Beyond 56 x 7: Expanding Mathematical Understanding
The simple problem of 56 x 7 serves as a springboard to explore more complex mathematical concepts:
-
Algebra: Multiplication forms the basis of algebraic equations and manipulations.
-
Geometry: Calculating areas and volumes often involves multiplication.
-
Calculus: Derivatives and integrals rely heavily on multiplication and its related operations.
Frequently Asked Questions (FAQ)
-
Q: What are some common mistakes students make when multiplying?
- A: Common errors include incorrect carrying over digits, misplacing place values, and forgetting to add the carried digit. A solid understanding of place value and careful attention to detail are crucial to avoid these mistakes.
-
Q: Are there other ways to break down 56 for easier multiplication?
- A: Yes, 56 can also be broken down as 40 + 16, or 7 x 8, which could lead to alternate calculation methods.
-
Q: How can I improve my multiplication skills?
- A: Consistent practice, focusing on understanding underlying principles rather than rote memorization, and exploring different calculation methods are key to improving multiplication skills. Utilizing online resources, games, and engaging with real-world applications can also enhance learning.
Conclusion: The Enduring Power of Multiplication
The seemingly straightforward calculation 56 x 7 unveils a wealth of mathematical principles and practical applications. From traditional multiplication methods to the distributive property and mental math techniques, we’ve explored various approaches to solving this problem, emphasizing the importance of understanding place value and the underlying mathematical concepts. This exploration extends beyond the immediate solution, providing insights into the historical development of multiplication and its enduring relevance in various fields. By grasping the fundamentals of multiplication, we not only solve numerical problems but also cultivate a deeper appreciation for the elegance and practicality of mathematics in our everyday lives. The more we understand the 'why' behind the 'how', the more confident and capable we become in tackling mathematical challenges of all kinds. Keep practicing, keep exploring, and unlock the full potential of mathematical understanding.
Latest Posts
Latest Posts
-
2 X 3x
Sep 22, 2025
-
28divided By 3
Sep 22, 2025
-
Itp Vs Ttp
Sep 22, 2025
-
10 X 365
Sep 22, 2025
-
40 Divide 3
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 56 X 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.