2 X 3x
interactiveleap
Sep 22, 2025 · 6 min read
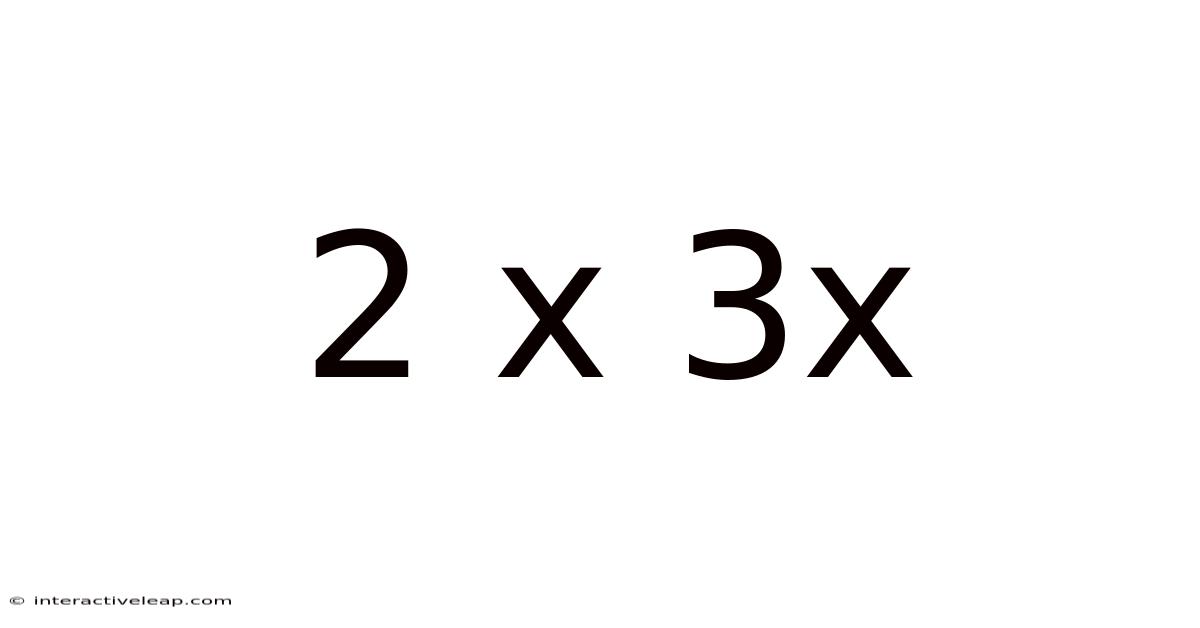
Table of Contents
Decoding 2 x 3x: A Deep Dive into the Mathematics of Multiplicative Growth
This article explores the mathematical expression "2 x 3x," delving beyond the simple multiplication to uncover its underlying principles and applications in various fields. We'll unpack the meaning, explore its implications within algebraic contexts, and examine its relevance in scenarios involving exponential growth, scaling, and even geometric sequences. Understanding "2 x 3x" opens doors to a broader comprehension of mathematical modeling and its real-world significance.
Understanding the Basics: What Does 2 x 3x Mean?
At its most fundamental level, "2 x 3x" represents a multiplication operation where the number 2 is multiplied by an unknown quantity, represented by "3x." The "x" acts as a variable, a placeholder for a numerical value. This expression highlights the concept of scaling, where a base value (2 in this case) is multiplied by a factor (3x) to obtain a new, larger value. The resulting product is dependent entirely on the value assigned to "x."
For instance:
- If x = 1, then 2 x 3x = 2 x 3(1) = 6
- If x = 2, then 2 x 3x = 2 x 3(2) = 12
- If x = 0, then 2 x 3x = 2 x 3(0) = 0
- If x = -1, then 2 x 3x = 2 x 3(-1) = -6
These examples demonstrate the variability inherent in the expression. The outcome is dynamic and directly responds to changes in the value of "x."
Algebraic Manipulation and Simplification
Within an algebraic context, "2 x 3x" can be simplified. Using the commutative and associative properties of multiplication, we can rewrite the expression as:
2 x 3 x x = 6x
This simplified form, "6x," is equivalent to the original expression and is often preferred for its conciseness. This simplification emphasizes the linear relationship between the final product and the variable "x." A change in "x" results in a directly proportional change in the final value. This linear relationship forms the backbone of numerous mathematical models, from simple calculations to complex simulations.
Applications in Real-World Scenarios: Exponential Growth and Scaling
While seemingly basic, the principles demonstrated by "2 x 3x" have wide-ranging applications. Let's explore some key examples:
1. Exponential Growth: Imagine a population of bacteria doubling every hour. If the initial population is represented by "x," after one hour we have 2x bacteria. After another hour, this population doubles again, yielding 2(2x) = 4x. While this specific example doesn't directly mirror "2 x 3x," the fundamental principle of multiplicative growth is analogous. The expression highlights how an initial value grows exponentially over time. Many phenomena, such as compound interest, population growth, and viral spread, exhibit this type of multiplicative growth.
2. Scaling and Proportionality: Consider a recipe that calls for 3x cups of flour. If you want to double the recipe (scaling factor of 2), you'd need 2(3x) = 6x cups of flour. This illustrates how "2 x 3x" can model scaling processes where an initial quantity is multiplied by a factor to obtain a proportionally larger or smaller amount. This principle is crucial in various fields, from engineering (scaling up designs) to manufacturing (adjusting production based on demand).
3. Geometric Sequences: The expression can be used to generate terms in a geometric sequence. A geometric sequence is characterized by a constant ratio between successive terms. If the first term is 2 and the common ratio is 3, the sequence would be:
2, 6, 18, 54, ...
Each term is obtained by multiplying the previous term by 3. While not directly "2 x 3x," the expression's structure embodies the core principle of multiplying a term by a constant factor to obtain the next term. Geometric sequences are used to model phenomena with constant growth rates, such as radioactive decay or compound interest.
Exploring Variations and Extensions
The core concept of "2 x 3x" can be expanded upon and adapted to more complex scenarios:
-
Multiple Variables: The expression could be extended to include more variables, such as "2 x 3x x y," representing a multiplicative relationship involving several unknown quantities. This would lead to a more multifaceted equation, where the final value depends on the values assigned to multiple variables.
-
Functions: The expression can be incorporated into functions. For instance, f(x) = 2 x 3x could define a function where the output value depends on the input value "x." This function represents a linear relationship and can be graphed to visualize the relationship between "x" and f(x).
-
Higher-Order Polynomials: By raising the "x" to higher powers, such as "2 x 3x²," we move beyond a linear relationship to a quadratic or even higher-order polynomial relationship. These are useful for modeling more complex phenomena, where the rate of growth or change isn't constant.
Advanced Applications and Mathematical Modeling
The seemingly simple equation "2 x 3x" serves as a building block for more intricate mathematical models. Here are some examples:
-
Economic Modeling: Economic growth models often incorporate multiplicative factors to represent the impact of various variables, such as investment, productivity, and technological progress. The fundamental idea of scaling and proportionality, embodied in "2 x 3x," plays a significant role.
-
Physics and Engineering: In physics and engineering, scaling laws are crucial in designing and analyzing systems. The principles underlying "2 x 3x" are vital in understanding how changes in one parameter affect others, leading to optimization and efficient design.
-
Computer Science: Algorithms and data structures often involve multiplicative operations. The concept of scaling is vital in analyzing algorithm efficiency and predicting their performance with varying input sizes.
Frequently Asked Questions (FAQ)
Q: What happens if 'x' is a fraction or a decimal?
A: The expression works the same way. Substitute the fractional or decimal value for "x," and perform the multiplication. The resulting value will be a reflection of the chosen value for "x."
Q: Can 'x' be a negative number?
A: Yes, "x" can be negative. However, this will result in a negative final value. The negative sign will indicate an inverse relationship or a decrease instead of an increase.
Q: What if the expression was "3x x 2"?
A: Due to the commutative property of multiplication, "3x x 2" is equivalent to "2 x 3x," and simplifies to 6x. The order of the multiplication doesn't affect the final result.
Q: How does this relate to more complex mathematical concepts?
A: "2 x 3x" provides a foundational understanding of variables, algebraic manipulation, proportionality, scaling, and multiplicative growth. These concepts are crucial in advanced topics such as calculus, linear algebra, differential equations, and various mathematical modeling techniques.
Conclusion: The Power of Simplicity
The seemingly simple expression "2 x 3x" is far more than just a basic multiplication problem. It encapsulates key mathematical principles that find applications across a wide array of fields. Understanding its implications – from simple scaling to modeling exponential growth and constructing geometric sequences – unlocks a deeper comprehension of how mathematics underpins our world. Its seemingly basic nature belies the profound power it holds in explaining and predicting a multitude of phenomena, reinforcing the elegance and universality of mathematics. The exploration of this seemingly straightforward expression offers a gateway to a richer understanding of the mathematical world and its vast applications.
Latest Posts
Latest Posts
-
Marine Expeditionary Brigade
Sep 22, 2025
-
Bronzino Venus Cupid
Sep 22, 2025
-
Single Section Ladder
Sep 22, 2025
-
50 Of 36
Sep 22, 2025
-
Dapper Dan Cannock
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2 X 3x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.