5 X 6
interactiveleap
Sep 14, 2025 · 6 min read
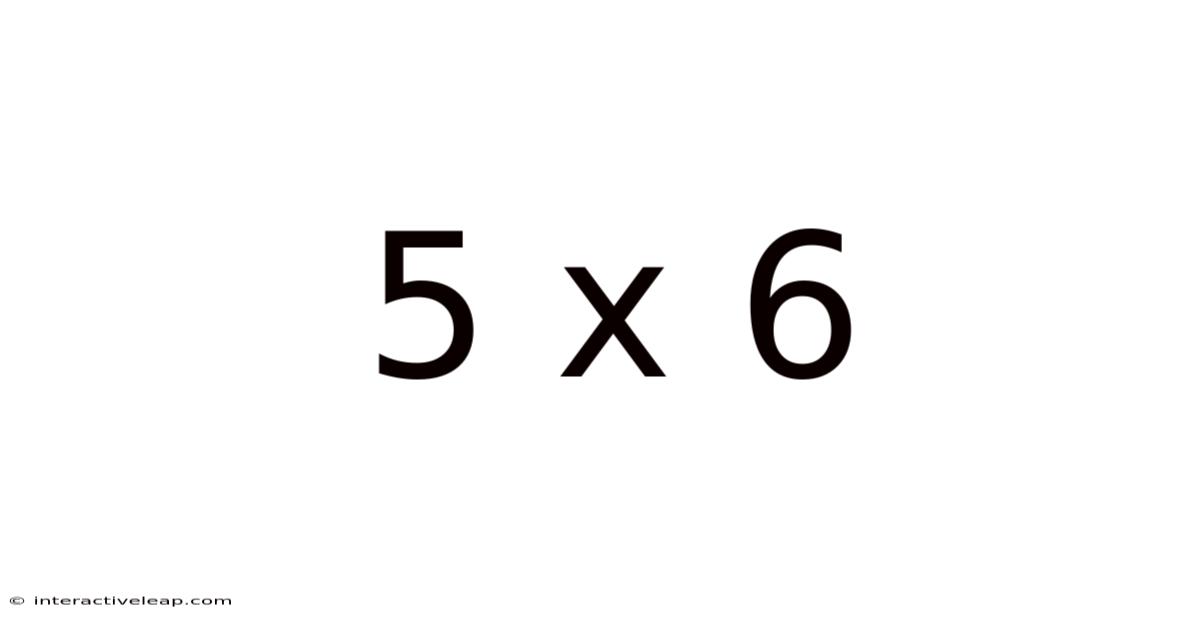
Table of Contents
Exploring the Multifaceted World of 5 x 6: From Simple Multiplication to Complex Applications
The seemingly simple expression "5 x 6" might appear insignificant at first glance. However, this fundamental mathematical concept opens doors to a surprisingly vast and interconnected landscape of knowledge, spanning arithmetic, geometry, algebra, and even real-world applications. This article delves deep into the world of 5 x 6, exploring its various facets and demonstrating its relevance across multiple disciplines. We will move beyond the basic calculation to explore the underlying principles, related concepts, and practical examples, making this a comprehensive guide for learners of all levels.
I. The Fundamentals: Understanding 5 x 6 = 30
At its core, 5 x 6 represents the mathematical operation of multiplication. It signifies adding the number 5 to itself six times: 5 + 5 + 5 + 5 + 5 + 5 = 30. This simple equation is the building block for more complex calculations. Understanding this foundational principle is critical for grasping more advanced mathematical concepts. Children often learn this through visual aids like counting objects arranged in arrays (5 rows of 6 objects each) or using manipulatives. The answer, 30, represents the total number of objects in this arrangement. The commutative property of multiplication also highlights that 5 x 6 is equivalent to 6 x 5, demonstrating the interchangeability of the multiplicands.
II. Visualizing 5 x 6: Geometric Representations
The equation 5 x 6 can be visually represented in several ways. Consider a rectangle with dimensions 5 units by 6 units. The area of this rectangle perfectly embodies 5 x 6, visually demonstrating that the product, 30, represents the total number of square units within the rectangle. This geometric representation provides a concrete, visual understanding of multiplication, making the abstract concept more tangible, particularly for younger learners. Further expanding on this, we can visualize it as five groups of six, arranging objects in a grid-like structure, reinforcing the idea of repeated addition.
III. 5 x 6 in Different Number Systems
While we commonly use the base-10 decimal system, understanding how 5 x 6 translates into other number systems provides a richer appreciation of mathematical principles. For instance, in the binary system (base-2), 5 is represented as 101 and 6 as 110. Multiplying these binary numbers requires a different approach, but the result, when converted back to base-10, will still be 30. Exploring this concept reveals the universality of mathematical operations regardless of the chosen number system. This expands our understanding of number systems and their interrelation, highlighting the underlying logic that remains consistent across different bases.
IV. Applications of 5 x 6 in Real-World Scenarios
The seemingly simple calculation 5 x 6 finds numerous practical applications in everyday life:
- Shopping: If you buy 5 items costing $6 each, the total cost will be $30. This simple application highlights the practical use of multiplication in daily transactions.
- Measurement: Imagine a rectangular garden with dimensions of 5 meters by 6 meters. The area of the garden would be 30 square meters. This demonstrates the application of 5 x 6 in calculating area, a crucial concept in geometry and many real-world problems.
- Time Management: If you spend 5 hours each day on a project for 6 days, you will have spent 30 hours on that project. This underscores the relevance of multiplication in time management and scheduling.
- Cooking: If a recipe calls for 5 ingredients, and you need to prepare 6 batches of that recipe, you'll need 30 ingredients in total. This shows how 5 x 6 can be applied in everyday cooking and meal preparation.
These examples showcase the ubiquitous nature of this simple mathematical calculation. It's not just a theoretical concept; it is a practical tool applied across various domains of life.
V. Extending the Concept: Factors and Multiples
The equation 5 x 6 allows us to explore related concepts like factors and multiples. The numbers 5 and 6 are factors of 30, meaning they divide evenly into 30. Conversely, 30 is a multiple of both 5 and 6. Understanding these relationships helps in simplifying fractions, solving algebraic equations, and comprehending more complex mathematical concepts. The exploration of factors and multiples builds a deeper understanding of number properties and their relationships. Prime factorization, for instance, further expands on this concept by breaking down numbers into their prime factors.
VI. 5 x 6 and its role in Algebra
Beyond arithmetic, 5 x 6 plays a role in algebra. It can be incorporated into algebraic expressions and equations. For example, the equation 5x = 30 can be easily solved to find the value of x (x = 6), demonstrating the connection between arithmetic and algebraic manipulations. This simple example illustrates how basic arithmetic operations form the foundations for solving more complex algebraic problems. The principles involved in solving this basic equation can be extended to more complex algebraic expressions and equations.
VII. Advanced Mathematical Concepts Related to 5 x 6
The seemingly simple calculation of 5 x 6 connects to various advanced mathematical concepts:
- Number Theory: The factors of 30 (1, 2, 3, 5, 6, 10, 15, 30) provide a basis for studying divisibility rules, prime factorization, and other concepts within number theory. The study of numbers and their properties forms a significant part of advanced mathematics.
- Combinatorics: If you have 5 choices for one item and 6 choices for another, you have 30 possible combinations. This showcases the link between multiplication and combinatorics, a branch of mathematics dealing with counting and arrangement problems.
- Probability: The calculation can be used to calculate probabilities in simple scenarios. For instance, if there's a 1/5 chance of event A happening and a 1/6 chance of event B happening, the probability of both events happening is 1/30.
These examples highlight the surprising depth and breadth of connections between this seemingly simple equation and more advanced mathematical concepts.
VIII. Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to learn 5 x 6?
- A: Visual aids like arrays of objects or using manipulatives are effective for younger learners. Repeated addition (5 + 5 + 5 + 5 + 5 + 5) is another simple approach.
-
Q: Are there any tricks to remember 5 x 6?
- A: Remembering that multiplying by 5 is the same as halving and multiplying by 10 can be helpful (6 x 10 = 60, then halve it to get 30). Alternatively, visualize a 5 x 6 rectangle and count the squares.
-
Q: Why is understanding 5 x 6 important?
- A: It's a fundamental building block for more complex mathematical calculations and has widespread practical applications in everyday life. It's essential for developing a strong foundation in mathematics.
-
Q: How can I apply 5 x 6 to more advanced math problems?
- A: Its principles are used in algebra, combinatorics, probability, and number theory, showcasing its relevance in various branches of mathematics.
IX. Conclusion
The seemingly simple multiplication problem 5 x 6 = 30 is far more than a basic arithmetic calculation. It serves as a gateway to understanding fundamental mathematical concepts and their far-reaching applications. From visualizing areas of rectangles to solving algebraic equations, understanding this core principle lays a strong foundation for further mathematical exploration. Its relevance extends beyond the classroom, finding practical application in various aspects of daily life. By exploring the various facets of 5 x 6, we've uncovered its significant role in the broader world of mathematics and its practical utility in our daily lives, solidifying its importance as a core mathematical concept. The journey from simple multiplication to understanding its complex interconnectedness showcases the beauty and power of mathematical principles.
Latest Posts
Latest Posts
-
800g In Kg
Sep 14, 2025
-
52kg To Stone
Sep 14, 2025
-
Poems About Praise
Sep 14, 2025
-
2 7kg To Lbs
Sep 14, 2025
-
8 Of 300
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 5 X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.