8 Of 300
interactiveleap
Sep 14, 2025 · 8 min read
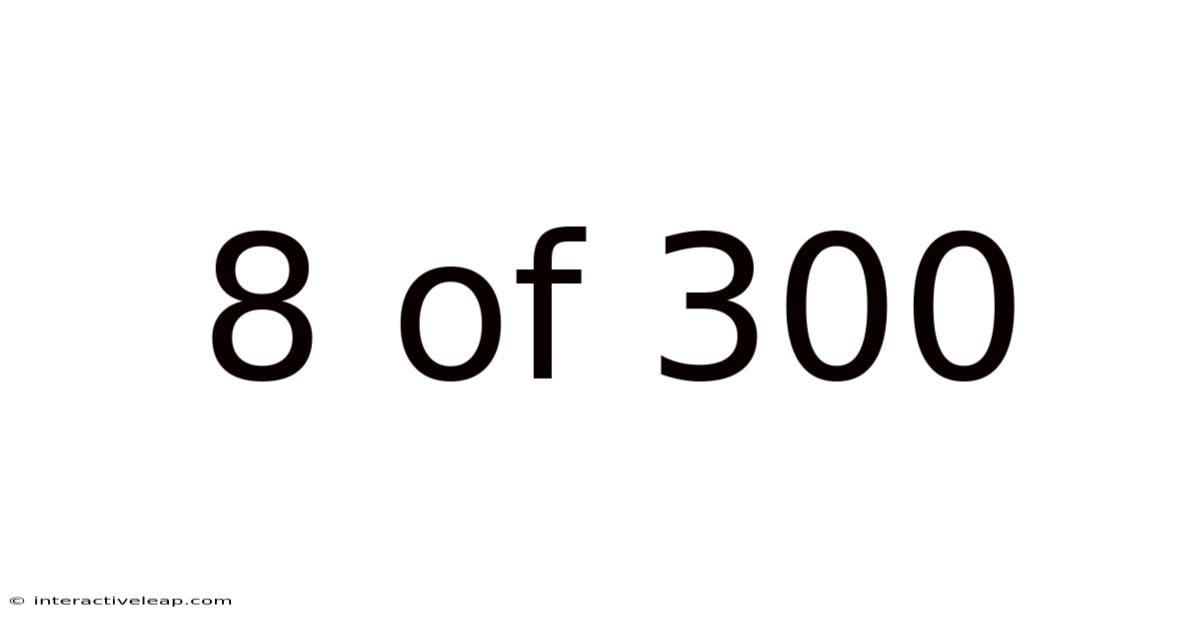
Table of Contents
Decoding the Enigma: Understanding the Significance of "8 of 300"
The phrase "8 of 300" might seem cryptic at first glance. It lacks the immediate context of a well-known idiom or historical event. However, depending on the field of study, this seemingly simple phrase can unlock a fascinating world of statistical analysis, strategic planning, and even philosophical contemplation. This article delves deep into the potential meanings and applications of "8 of 300," exploring its significance across various disciplines and highlighting its implications for decision-making. Understanding the context is key to unlocking the true meaning behind this enigmatic phrase.
Introduction: The Context Matters
The number "8 out of 300" represents a proportion or ratio. Its interpretation hinges entirely on the context within which it's presented. Without knowing what the "8" and the "300" represent, we can only speculate on its meaning. Is it 8 successful trials out of 300 attempts? 8 defective products in a batch of 300? 8 positive responses in a survey of 300 participants? The possibilities are endless. The context will dictate the interpretation and influence how we analyze its significance.
Scenario 1: Statistical Significance in Research
Let's imagine "8 of 300" represents the number of participants in a clinical trial who experienced a specific side effect after taking a new medication. In this context, we would analyze the data using statistical methods to determine the significance of this result.
Understanding Statistical Significance:
-
Proportion: The basic proportion is 8/300 = 0.0267, or approximately 2.67%. This tells us that about 2.67% of participants experienced the side effect.
-
Confidence Intervals: We would then calculate confidence intervals around this proportion to estimate the range within which the true population proportion likely lies. A 95% confidence interval would provide a range within which we are 95% certain that the true proportion lies. The width of this interval depends on the sample size (300 in this case) and the observed proportion (2.67%).
-
Hypothesis Testing: We might have a pre-defined hypothesis, such as "the incidence of this side effect is less than 5%." We would then conduct a hypothesis test (e.g., a one-sample proportion z-test) to determine whether our observed proportion of 2.67% provides sufficient evidence to reject this hypothesis. The p-value obtained from this test would indicate the probability of observing a proportion as extreme as 2.67% if the null hypothesis (incidence less than 5%) were true.
-
Sample Size: The relatively small number of participants who experienced the side effect (8) compared to the total sample size (300) is crucial. A larger sample size would provide more precise estimates and potentially lead to different conclusions about the statistical significance of the observed side effect.
Conclusion in a Research Context: Based on the statistical analysis, we could conclude whether the observed side effect is statistically significant, clinically relevant, or simply a chance occurrence. This information would be crucial for deciding whether the medication should be approved, further tested, or withdrawn from the market.
Scenario 2: Quality Control in Manufacturing
In a manufacturing setting, "8 of 300" could represent the number of defective items found in a batch of 300. This would be a critical quality control metric.
Analyzing Defects:
-
Defect Rate: The defect rate is 8/300 = 2.67%, similar to the previous example.
-
Acceptable Quality Level (AQL): Manufacturing processes typically have an AQL, which is the maximum percentage of defective items considered acceptable. If the 2.67% defect rate exceeds the AQL, then corrective action is needed. This could involve investigating the manufacturing process, identifying the root cause of the defects, and implementing improvements to reduce the defect rate.
-
Process Capability: The defect rate can be used to assess the capability of the manufacturing process to meet quality standards. Statistical process control (SPC) techniques would be employed to monitor the defect rate over time and identify trends or shifts indicating process instability.
-
Cost of Quality: A higher defect rate can lead to increased costs associated with rework, scrap, warranty claims, and customer dissatisfaction. The cost associated with the 8 defective items would need to be considered, and improvements in the process may be justifiable based on a cost-benefit analysis.
Conclusion in a Manufacturing Context: In quality control, understanding the significance of "8 of 300" helps identify potential problems within the manufacturing process. Addressing these issues promptly can improve product quality, reduce costs, and enhance customer satisfaction.
Scenario 3: Strategic Decision-Making in Business
Imagine "8 of 300" represents the number of customers who responded positively to a new marketing campaign out of a total of 300 targeted customers.
Evaluating Marketing Effectiveness:
-
Conversion Rate: The conversion rate is 8/300 = 2.67%. This indicates a low conversion rate.
-
Return on Investment (ROI): To determine the effectiveness of the campaign, the cost of the campaign needs to be compared to the revenue generated by the 8 converted customers. If the ROI is negative, the campaign is considered unsuccessful and adjustments are needed.
-
Market Segmentation: The data might suggest that the targeted group of 300 customers is not the ideal segment for the product or service. Further market research might be necessary to identify more responsive customer segments.
-
Campaign Optimization: A low conversion rate could indicate problems with the marketing message, the channel used, or the targeting strategy. Analyzing the data can help pinpoint areas for improvement and optimize future campaigns.
Conclusion in a Business Context: In business, "8 of 300" can signify the need for a deeper analysis of marketing strategies, customer segmentation, and overall campaign effectiveness. Understanding the reasons behind the low conversion rate is crucial for maximizing ROI and achieving business objectives.
Scenario 4: Probability and Chance
Beyond specific applications, "8 of 300" can be examined through the lens of probability and chance.
Understanding Probability:
-
Probability of Success: If the "8" represents successful events and the "300" represents total attempts, the probability of success on a single trial is approximately 2.67%. This probability is relatively low.
-
Expected Value: If we consider this a random process (e.g., flipping a biased coin), we can calculate the expected value of successes in 300 trials as 300 * 0.0267 ≈ 8. This confirms that the observed outcome (8 successes) is close to what we'd expect given the probability.
-
Rare Events: A low probability event like this doesn't necessarily indicate something unusual or significant. Pure chance could account for the observation. However, if such a low probability event is repeated consistently, it could warrant further investigation.
Conclusion from a Probability Perspective: Analyzing "8 of 300" from a probabilistic viewpoint reminds us that seemingly unusual outcomes can sometimes arise purely by chance. Careful consideration is needed to distinguish between random fluctuation and truly significant occurrences.
Scenario 5: The Philosophical Perspective
Finally, viewing "8 of 300" philosophically, we can consider the meaning of small numbers within a larger context. This can lead to discussions about:
-
Significance vs. Insignificance: Is a small number inherently insignificant, or can it hold profound meaning depending on the context? The 8 could represent a pivotal moment, a crucial discovery, or a small act with far-reaching consequences.
-
The Power of the Few: The 8 could symbolize the influence of a minority, a small group of people or events that significantly impact the larger 300. This perspective touches upon themes of leadership, innovation, and social change.
-
Perspective and Scale: The importance of "8 of 300" is relative. Viewed from a grander perspective, the 8 might seem insignificant, but within a more focused context, it could be extraordinarily meaningful.
Conclusion from a Philosophical Perspective: Considering "8 of 300" philosophically invites us to reflect on the interplay between small and large, the power of individual events, and the diverse ways we assign meaning to numbers.
Frequently Asked Questions (FAQ)
-
How do I calculate the percentage from "8 of 300"? Simply divide 8 by 300 and multiply by 100: (8/300) * 100 = 2.67%.
-
What statistical tests can I use to analyze "8 of 300"? Depending on the context, you could use a one-sample proportion z-test, chi-square test, or other relevant statistical tests.
-
What if "8 of 300" is a completely different context, say, 8 successes in a game of 300 attempts? The analysis would depend on the specific game rules and probabilities involved. You would analyze the data accordingly using appropriate statistical methods or probability calculations.
Conclusion: The Power of Context
The phrase "8 of 300" is, in itself, meaningless. Its significance entirely depends on the context in which it is presented. We have explored several scenarios illustrating how this seemingly simple phrase can be analyzed and interpreted across diverse fields. Understanding the context, applying appropriate statistical or analytical tools, and considering the broader implications are crucial for deciphering the true meaning and impact of "8 of 300." The seemingly small number, when placed within its appropriate context, can reveal surprising insights and inform crucial decision-making across various domains. Always remember, the numbers only tell part of the story; it's the context that breathes life into the data.
Latest Posts
Latest Posts
-
73inches In Feet
Sep 14, 2025
-
Uniform Layer Haircut
Sep 14, 2025
-
Baby Hair Brush
Sep 14, 2025
-
Winkel Tripel Projection
Sep 14, 2025
-
Geography Acrostic Poem
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 8 Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.