5 X 2x
interactiveleap
Sep 24, 2025 · 5 min read
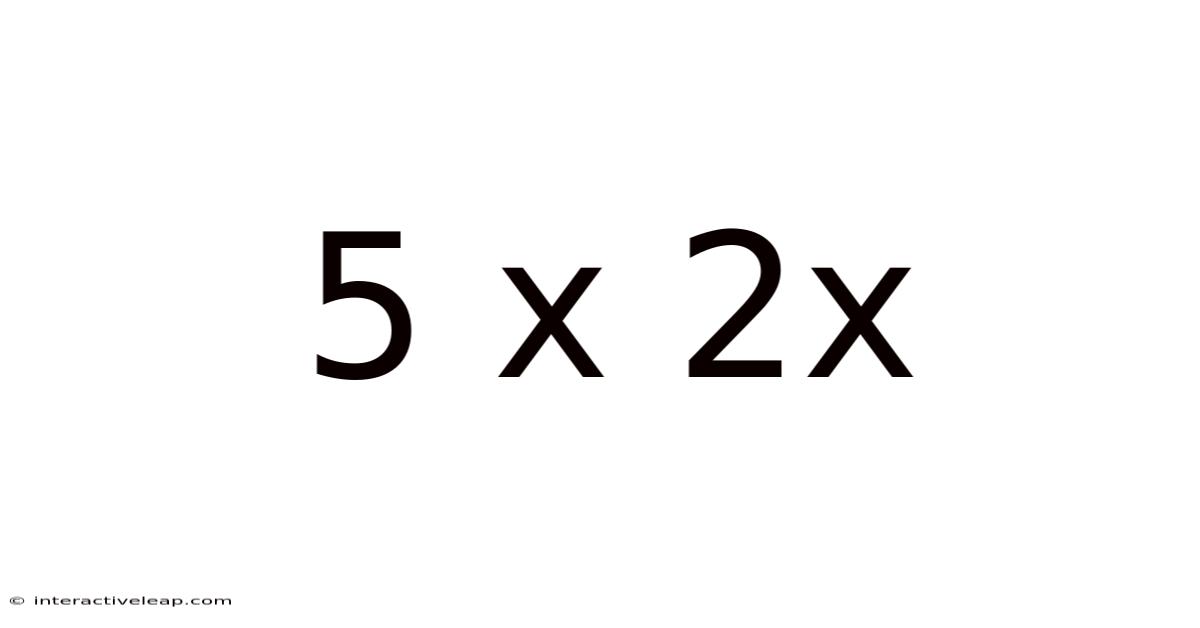
Table of Contents
Decoding 5 x 2x: Exploring the Multifaceted Nature of a Simple Expression
This article delves into the seemingly simple mathematical expression "5 x 2x," unraveling its various interpretations and applications across different fields. We'll move beyond the basic arithmetic to explore its significance in algebra, calculus, and even its potential representations in programming and other contexts. Understanding this expression requires us to unpack its components and appreciate how seemingly simple equations can possess surprising depth. This exploration is suitable for anyone from high school students brushing up on their algebra to those curious about the broader applications of mathematical notation.
Understanding the Basics: Arithmetic Interpretation
At its most fundamental level, "5 x 2x" represents a straightforward multiplication problem. In arithmetic, we typically interpret this as multiplying 5 by the variable '2x'. This is a crucial starting point, but it's just the tip of the iceberg. To evaluate this expression, we need to know the value of 'x'.
Let's consider a few examples:
- If x = 1: 5 x 2(1) = 5 x 2 = 10
- If x = 2: 5 x 2(2) = 5 x 4 = 20
- If x = 3: 5 x 2(3) = 5 x 6 = 30
These examples demonstrate the simple arithmetic interpretation: we substitute the value of 'x' into the expression and perform the multiplication. The result will always be ten times the value of x.
Stepping into Algebra: Variables and Expressions
In algebra, the expression "5 x 2x" is viewed slightly differently. Here, 'x' is not just a number waiting to be substituted, but a variable representing an unknown quantity. The expression itself is considered a linear expression because the highest power of the variable 'x' is 1.
We can simplify this algebraic expression using the commutative and associative properties of multiplication:
5 x 2x = 5 x 2 x x = 10x
This simplified form, 10x, is equivalent to the original expression and is much more concise. This simplification highlights a key aspect of algebra: finding equivalent, but more manageable, representations of expressions. This ability to manipulate and simplify expressions is fundamental to solving algebraic equations and tackling more complex problems.
Expanding Horizons: Applications in Calculus
While the arithmetic and algebraic interpretations are relatively straightforward, the expression "5 x 2x" takes on further significance when we move into the realm of calculus. Here, 'x' might represent a variable that changes continuously. This opens up the possibility of exploring concepts like differentiation and integration.
-
Differentiation: If we consider the expression 5 x 2x as a function, say f(x) = 10x, then finding its derivative, f'(x), provides the instantaneous rate of change of the function with respect to x. The derivative of 10x is simply 10. This indicates that the function f(x) = 10x has a constant rate of change of 10.
-
Integration: Conversely, integrating the expression 10x would give us the area under the curve of the function. The indefinite integral of 10x is 5x² + C, where C is the constant of integration. This highlights how the simple expression can be a building block for understanding more complex concepts in calculus.
Beyond Mathematics: Programming and Other Contexts
The expression "5 x 2x" can also appear in other contexts, particularly in programming. In many programming languages, the "*" symbol represents multiplication, and 'x' could be a variable holding a numerical value. The expression would be evaluated according to the programming language's rules of precedence and order of operations.
Consider a simple code snippet (pseudocode):
x = 5;
result = 5 * 2 * x;
print(result); // Output: 50
This example shows how the expression translates directly into a programming context. The flexibility of the expression highlights its adaptability across different disciplines.
Exploring Related Concepts: Linear Equations and Functions
Understanding "5 x 2x" also provides a foundation for grappling with related concepts, such as linear equations and functions. The simplified form, 10x, represents a linear function where the output (y) is directly proportional to the input (x). This relationship is fundamental to many scientific models and real-world phenomena.
Practical Applications: Real-World Examples
The principles underlying the expression "5 x 2x" have countless practical applications. For example:
-
Calculating Costs: If 'x' represents the number of units of a product costing $2 each, and there's a fixed cost of $5, then "5 + 2x" would represent the total cost. Understanding this type of equation is crucial in various business and financial contexts.
-
Geometric Calculations: In geometry, 'x' might represent the length of a side of a shape, and the expression could be part of a formula for calculating area or volume.
-
Physics and Engineering: Linear relationships are common in many areas of physics and engineering. For example, Hooke's Law (for springs) states that the force is proportional to the extension. This could be expressed using a similar linear relationship.
-
Data Analysis: In data analysis, linear relationships are often studied using linear regression techniques. Understanding linear expressions is foundational to interpreting and modelling such relationships.
Frequently Asked Questions (FAQs)
Q: What happens if 'x' is zero?
A: If x = 0, then 5 x 2x = 5 x 2(0) = 0. The entire expression evaluates to zero.
Q: Can 'x' be a negative number?
A: Yes, 'x' can be any real number, including negative numbers. For example, if x = -2, then 5 x 2x = 5 x 2(-2) = -20.
Q: What if the expression was written as (5 x 2)x?
A: According to the order of operations (PEMDAS/BODMAS), the multiplication within the parentheses would be performed first. (5 x 2)x = 10x, which is the same simplified form as 5 x 2x.
Q: Is there a limit to the value of 'x'?
A: Mathematically, there's no inherent limit to the value of 'x'. It can be any real number, positive or negative, including fractions and irrational numbers. However, practical applications might impose limitations based on the context of the problem.
Conclusion: The Power of Simplicity
The seemingly simple expression "5 x 2x" reveals a surprising depth of meaning and application. From basic arithmetic to advanced calculus and programming, its interpretation adapts to the context. Understanding this expression isn't just about getting the right answer; it's about appreciating the power of mathematical notation and its ability to represent complex relationships in a concise and elegant way. By mastering the fundamentals of this simple expression, we build a stronger foundation for understanding more intricate mathematical concepts and their real-world applications. This journey from a basic multiplication problem to understanding its relevance across multiple disciplines underlines the inherent beauty and power of mathematics.
Latest Posts
Latest Posts
-
10ml Into Mg
Sep 24, 2025
-
Spit And Kissing
Sep 24, 2025
-
11 20 In Decimal
Sep 24, 2025
-
0 83 In Fraction
Sep 24, 2025
-
Comparative Advantage Example
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 5 X 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.