11/20 In Decimal
interactiveleap
Sep 24, 2025 · 5 min read
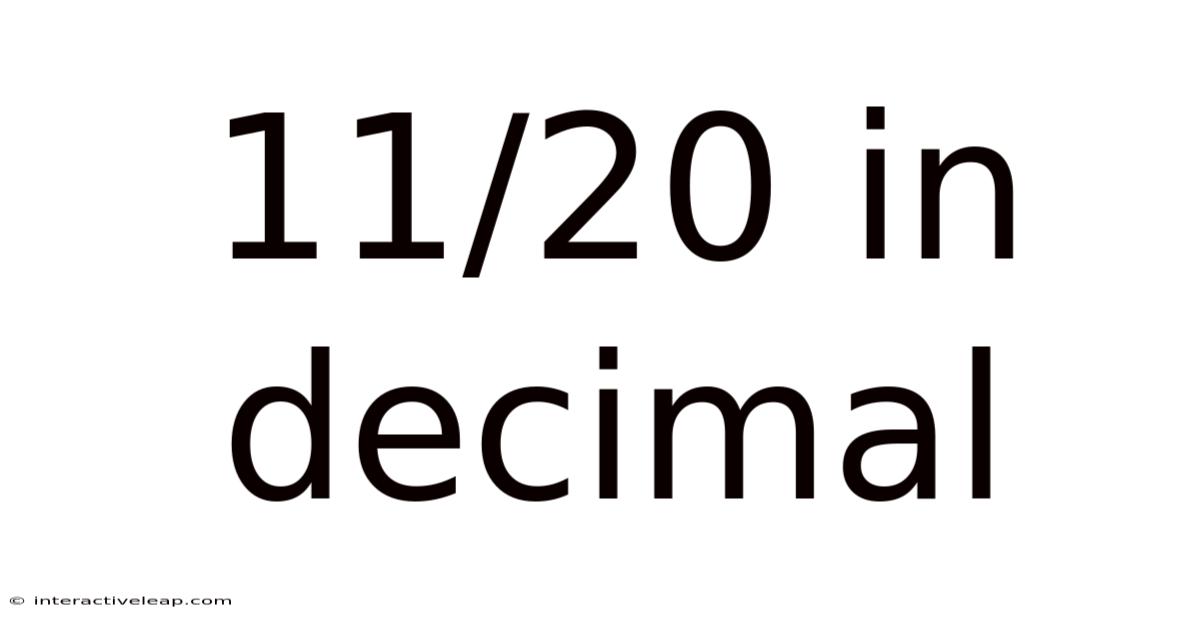
Table of Contents
Decoding 11/20: A Comprehensive Guide to Fractions and Decimals
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This article dives deep into converting the fraction 11/20 into its decimal form, exploring the underlying principles and offering practical applications. We'll cover various methods for conversion, address common misconceptions, and provide a solid foundation for tackling similar fractional conversions. This comprehensive guide will equip you with the knowledge to confidently handle fractions and decimals in various contexts.
Introduction: Why Understand 11/20 as a Decimal?
The fraction 11/20 represents eleven twentieths of a whole. While this fractional representation is perfectly valid, expressing it as a decimal – a number based on powers of ten – often offers advantages in practical calculations and comparisons. Decimals are commonly used in everyday life, from financial transactions (calculating percentages, for example) to scientific measurements and engineering applications. Knowing how to convert fractions like 11/20 into decimals is crucial for seamless transitions between these two essential mathematical representations. This article will serve as your complete guide to understanding this conversion process and its implications.
Method 1: Direct Division
The most straightforward method for converting a fraction to a decimal is through direct division. In the case of 11/20, this involves dividing the numerator (11) by the denominator (20).
- Step 1: Set up the division problem: 11 ÷ 20
- Step 2: Since 11 is smaller than 20, add a decimal point to 11 and a zero to make it 11.0. This doesn't change the value; it simply allows for the division process.
- Step 3: Now perform the long division. 20 goes into 110 five times (20 x 5 = 100).
- Step 4: Subtract 100 from 110, leaving a remainder of 10.
- Step 5: Add another zero to the remainder, making it 100.
- Step 6: 20 goes into 100 five times (20 x 5 = 100).
- Step 7: The remainder is zero, indicating the division is complete.
Therefore, 11/20 = 0.55.
Method 2: Equivalent Fractions and Decimal Conversion
Another effective method involves converting the fraction into an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). This allows for a direct conversion to a decimal.
- Step 1: Find a number that, when multiplied by the denominator (20), results in a power of 10. In this case, multiplying 20 by 5 gives 100.
- Step 2: To maintain the equivalence of the fraction, multiply both the numerator and the denominator by 5: (11 x 5) / (20 x 5) = 55/100
- Step 3: A fraction with a denominator of 100 can be easily converted to a decimal. 55/100 represents 55 hundredths, which is written as 0.55.
This method highlights the underlying principle of maintaining the proportional value of the fraction while altering its representation.
Method 3: Using a Calculator
While not as conceptually enlightening as the previous methods, using a calculator provides a quick and efficient way to convert fractions to decimals. Simply input 11/20 into the calculator and press the equals button. The result will be 0.55. This method is particularly useful for more complex fractions where long division becomes cumbersome.
Understanding the Decimal Value: 0.55
The decimal 0.55 represents fifty-five hundredths. This can be further broken down as:
- 5 tenths (0.5)
- 5 hundredths (0.05)
This decimal value highlights the magnitude of the fraction 11/20 within the context of a whole unit. It signifies a value that is slightly more than half (0.5 or 50%).
Practical Applications of 11/20 and 0.55
The knowledge of converting 11/20 to 0.55 has numerous practical applications across various fields:
- Finance: Calculating discounts, interest rates, or proportions of investments. For instance, an 11/20 discount on a $100 item would be $55.
- Measurement: Representing portions of lengths, weights, volumes, or other measurable quantities.
- Statistics: Expressing proportions in data analysis, such as the percentage of respondents who answered a particular way in a survey.
- Everyday Life: Dividing quantities fairly amongst a group of people, calculating portions for recipes, or determining the amount of a substance needed for a given task.
Common Misconceptions about Fraction-to-Decimal Conversions
- Incorrect Division: A common mistake is incorrectly performing the division, leading to an inaccurate decimal representation. Carefully following the steps of long division or using a calculator accurately is essential.
- Improper Simplification: Before attempting conversion, ensuring the fraction is simplified to its lowest terms can prevent unnecessary complications during the conversion process. While 11/20 is already in its simplest form, understanding this principle is crucial when working with other fractions.
- Misinterpreting Decimal Places: Understanding the place value of digits in a decimal is crucial for correct interpretation. For instance, misinterpreting 0.55 as 5.5 would represent a completely different magnitude.
Frequently Asked Questions (FAQs)
-
Q: Can all fractions be converted to terminating decimals?
- A: No, only fractions whose denominators can be expressed as a product of 2 and 5 (or powers of 2 and 5) will result in terminating decimals. Other fractions will result in repeating decimals.
-
Q: What if the division doesn't end with a zero remainder?
- A: If the remainder continues to repeat, the decimal is a repeating decimal. This is denoted by placing a bar above the repeating digits. For example, 1/3 = 0.333... (or 0.3̅).
-
Q: What are some alternative methods for converting fractions to decimals?
- A: Beyond the methods described, you can also use fraction-to-decimal conversion tables or online converters. However, it's highly beneficial to understand the underlying mathematical principles.
-
Q: How can I improve my understanding of fractions and decimals?
- A: Practice regularly by working through various conversion examples. Use online resources, textbooks, and worksheets to reinforce your knowledge.
Conclusion: Mastering Fraction-to-Decimal Conversions
Understanding the conversion of fractions to decimals, exemplified by the conversion of 11/20 to 0.55, is a cornerstone of mathematical proficiency. This skill is not limited to theoretical exercises; it finds practical application in everyday life, across various professional fields, and within more advanced mathematical studies. By mastering this fundamental concept, you enhance your ability to navigate mathematical problems with confidence and accuracy. Remember to practice regularly and reinforce your understanding through diverse examples and applications to solidify your grasp of this crucial skill. The methods outlined in this article—direct division, equivalent fractions, and calculator usage—offer versatile approaches to solve such problems, catering to different learning styles and preferences. Choosing the method that best suits your understanding will ensure a thorough grasp of this critical mathematical concept.
Latest Posts
Latest Posts
-
69 Fahrenheit Celsius
Sep 24, 2025
-
1 75 In Feet
Sep 24, 2025
-
Teams Or Teams
Sep 24, 2025
-
85cm In Ft
Sep 24, 2025
-
Hair Extension Methods
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 11/20 In Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.