5 Of 1000000
interactiveleap
Sep 15, 2025 · 7 min read
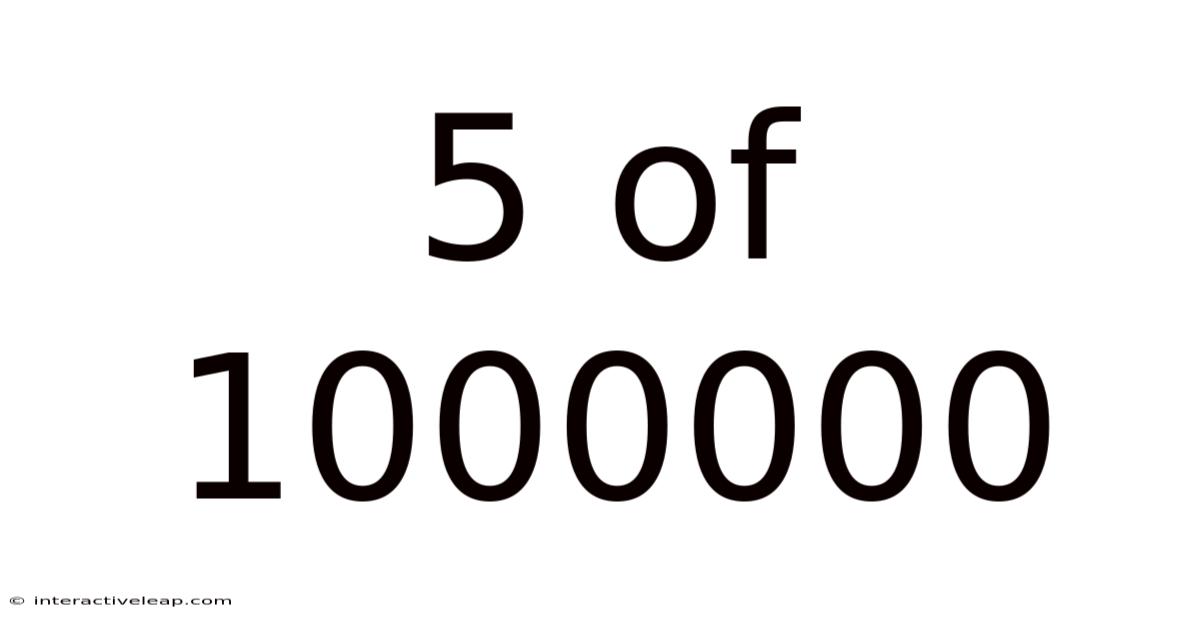
Table of Contents
Decoding the Infinitesimal: Exploring the Significance of 5 out of 1,000,000
Understanding the concept of probability and its impact on our lives is crucial, whether we're analyzing scientific data, making financial decisions, or simply navigating everyday uncertainties. This article delves into the seemingly insignificant number of 5 out of 1,000,000, exploring its mathematical representation, contextual significance, and applications across various fields. We'll uncover why even such a small probability can hold immense importance and how understanding it enhances our critical thinking skills. This exploration will reveal that the seemingly minuscule fraction of 5/1,000,000 is far more significant than it initially appears.
Introduction: The Power of Small Probabilities
The phrase "5 out of 1,000,000" immediately evokes a sense of rarity. It represents a minuscule probability, a tiny fraction within a vast whole. Yet, this seemingly insignificant number carries considerable weight, especially when considering contexts like risk assessment, statistical analysis, and the understanding of large-scale events. This article aims to illuminate the mathematical implications of this fraction, explore its real-world applications, and demonstrate why even extremely low probabilities warrant careful consideration. We will move beyond simple numerical representation and delve into the underlying concepts that make this seemingly small number surprisingly impactful.
Mathematical Representation and Contextualization
Mathematically, 5 out of 1,000,000 is represented as the fraction 5/1,000,000, which simplifies to 1/200,000. This fraction can also be expressed as a decimal (0.000005) or a percentage (0.0005%). The significance of this number, however, transcends its simple numerical representation. Its meaning depends heavily on the context in which it is applied.
Consider these examples:
-
Lottery Wins: Winning a lottery with odds of 1 in 200,000 is extremely unlikely. While the probability is low, it's not impossible. Millions of people participate in lotteries, increasing the chance that someone will win.
-
Disease Prevalence: If a disease affects 1 in 200,000 individuals, it's considered rare. However, in a large population, even a rare disease can affect a considerable number of people. Public health initiatives often focus on rare diseases to prevent outbreaks and provide timely interventions.
-
Manufacturing Defects: A manufacturing process with a defect rate of 1 in 200,000 might seem acceptable at first glance. However, in mass production, even a small defect rate can lead to a significant number of faulty products, impacting the company's reputation and potentially causing harm to consumers.
-
Scientific Research: In scientific experiments involving large datasets, a result with a p-value (probability of obtaining the result by chance) of 0.000005 would generally be considered statistically significant, indicating strong evidence against the null hypothesis.
These examples illustrate that the contextual application dictates the interpretation of the probability. A small probability can have significant consequences depending on the scale and impact of the event.
Exploring the Concept of Probability and Statistical Significance
The probability of an event occurring is expressed as a number between 0 and 1, where 0 indicates impossibility and 1 indicates certainty. The probability of 5 out of 1,000,000 falls squarely within the realm of low-probability events. However, the concept of statistical significance complicates this further.
Statistical significance tests whether an observed result is likely due to chance or a real effect. A p-value represents the probability of obtaining the observed results (or more extreme results) if the null hypothesis (the assumption that there is no effect) is true. In many scientific fields, a p-value below 0.05 is often considered statistically significant, implying strong evidence against the null hypothesis. Our probability of 0.000005 would be highly statistically significant in most research settings.
This highlights the crucial distinction between a low probability and statistical significance. While a low probability suggests rarity, statistical significance provides evidence for a real effect or a departure from a null hypothesis.
Real-World Applications: From Risk Assessment to Healthcare
The concept of 5 out of 1,000,000 has profound implications across numerous disciplines:
1. Risk Assessment and Management: In industries like aviation and nuclear power, risk assessment involves quantifying and managing low-probability, high-consequence events. Even events with minuscule probabilities can have devastating consequences, requiring meticulous safety protocols and risk mitigation strategies.
2. Healthcare and Epidemiology: Epidemiologists study the spread and control of diseases. Understanding the probability of disease transmission, particularly for rare diseases, is crucial for developing effective prevention and treatment strategies. Predictive modeling often incorporates probabilities to estimate disease outbreaks and allocate resources effectively.
3. Financial Modeling and Investment: In finance, risk assessment is paramount. Investors utilize probabilities to assess the likelihood of investment success or failure, employing sophisticated models to predict market trends and manage risk.
4. Environmental Science: Analyzing the probability of environmental disasters, such as oil spills or nuclear accidents, helps in developing effective response plans and preventative measures. Environmental risk assessments often involve complex probabilistic models that consider multiple factors.
5. Quality Control in Manufacturing: Maintaining high product quality requires rigorous testing and quality control measures. Probabilistic models can help manufacturers predict defect rates and implement strategies to minimize production failures.
The Psychology of Probability: Perceptions vs. Reality
Human perception of probability often deviates from mathematical reality. We tend to overestimate the likelihood of highly publicized events, such as plane crashes, while underestimating the probability of more common but less dramatic events, like car accidents. This cognitive bias, known as the availability heuristic, can lead to flawed decision-making. Understanding the true probability of events, even those with seemingly insignificant chances, is essential for making rational choices.
Furthermore, the human tendency towards confirmation bias further complicates our interpretation of probabilities. We tend to seek out and interpret information that confirms our pre-existing beliefs, even if that information is statistically improbable. This can lead to misinterpretations of data and faulty conclusions.
Beyond the Numbers: The Importance of Context and Critical Thinking
The number 5 out of 1,000,000 is not merely a numerical value; it's a representation of a probability that requires critical analysis within its specific context. To fully grasp its significance, we must consider:
-
The scale of the population or sample size: A probability of 5/1,000,000 might represent a significant number of occurrences in a large population.
-
The consequences of the event: The impact of an event with a low probability can be substantial if the consequences are severe.
-
The available mitigation strategies: Understanding the probability of an event allows us to develop appropriate mitigation strategies to reduce its impact.
-
The limitations of data and models: Probabilistic predictions are based on available data and models, which may not be perfect. Understanding these limitations is essential for interpreting results accurately.
Frequently Asked Questions (FAQ)
Q: How can I calculate the probability of an event?
A: The probability of an event is calculated by dividing the number of favorable outcomes by the total number of possible outcomes. In the case of 5 out of 1,000,000, the probability is 5/1,000,000 or 1/200,000.
Q: What is the difference between probability and statistics?
A: Probability deals with predicting the likelihood of future events based on known parameters. Statistics involves analyzing data from past events to draw inferences about populations or make predictions. They are closely related fields.
Q: How do I interpret a p-value in scientific research?
A: A p-value represents the probability of observing the results (or more extreme results) if the null hypothesis is true. A low p-value (typically below 0.05) suggests strong evidence against the null hypothesis. However, it doesn't prove the alternative hypothesis is true.
Q: Can a low probability event happen?
A: Yes, even events with extremely low probabilities can and do occur. The probability reflects the likelihood, not the certainty, of an event happening.
Conclusion: The Significance of the Infinitesimal
The seemingly insignificant number 5 out of 1,000,000 carries considerable weight when considered within the appropriate context. Understanding this small probability enhances our ability to analyze data, assess risks, and make informed decisions. While the number itself might appear negligible, its implications across diverse fields, from healthcare and finance to environmental science and manufacturing, highlight the crucial role of probability and statistics in our world. This exploration reinforces the idea that even the smallest probabilities can have significant consequences, emphasizing the importance of critical thinking and careful consideration when interpreting numerical data and making informed choices. The seemingly infinitesimal can, in fact, hold immense significance.
Latest Posts
Latest Posts
-
Magnesium Sulfide Formula
Sep 15, 2025
-
225lbs In Kg
Sep 15, 2025
-
130 Kmh Mph
Sep 15, 2025
-
34 Of 20
Sep 15, 2025
-
10000 60
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 5 Of 1000000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.