34 Of 20
interactiveleap
Sep 15, 2025 · 6 min read
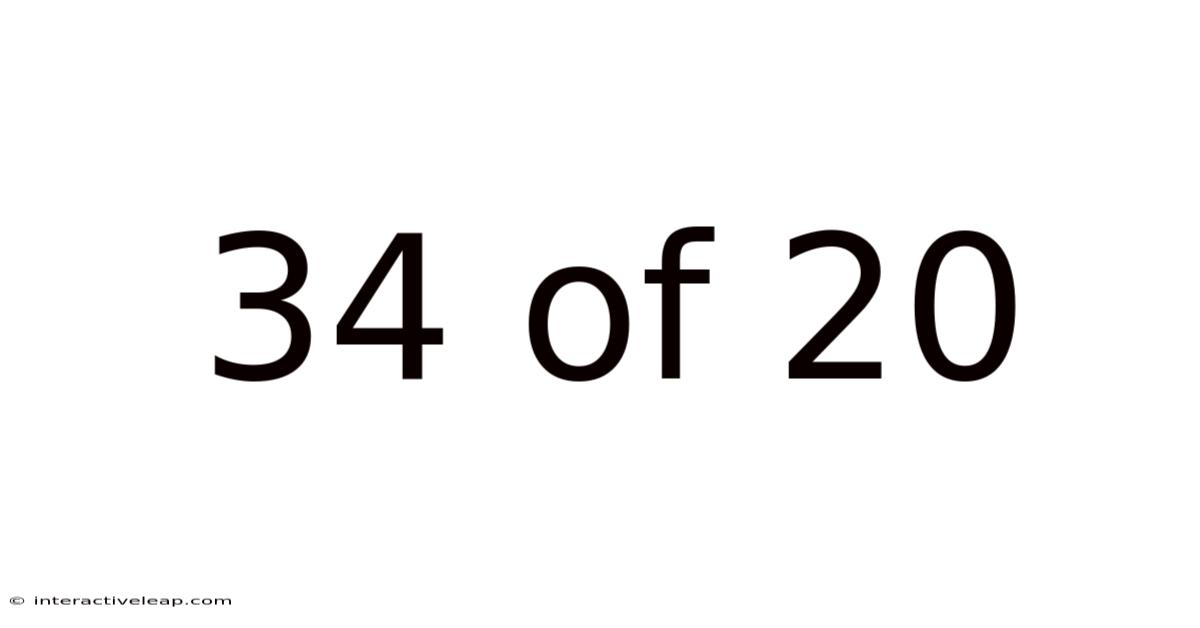
Table of Contents
Decoding 34 of 20: Understanding Odds, Probability, and Their Applications
The phrase "34 of 20" might initially seem nonsensical. How can something be 34 out of 20? This seemingly contradictory statement actually unveils a deeper understanding of odds, probability, and their applications across various fields, from gambling and sports to finance and even weather forecasting. This article will delve into the meaning behind such expressions, explaining the underlying mathematical concepts and showcasing real-world examples.
Understanding Odds and Probability
Before diving into the specifics of "34 of 20," let's clarify the fundamental concepts of odds and probability. These terms are often used interchangeably, but they represent different aspects of chance.
-
Probability: Probability represents the likelihood of an event occurring. It's expressed as a fraction or decimal between 0 and 1, where 0 means the event is impossible, and 1 means the event is certain. For example, the probability of flipping a fair coin and getting heads is 1/2 or 0.5.
-
Odds: Odds represent the ratio of the likelihood of an event occurring to the likelihood of it not occurring. Odds are usually expressed as a ratio (e.g., 3:1) or a fraction (e.g., 3/1). In the coin flip example, the odds of getting heads are 1:1 (or 1/1), meaning the chances of getting heads are equal to the chances of getting tails.
The relationship between probability (P) and odds (O) is as follows:
- Odds in favor: O = P / (1 - P)
- Odds against: O = (1 - P) / P
Therefore, if the probability of an event is 1/3, the odds in favor are 1:2, and the odds against are 2:1.
Interpreting "34 of 20" – The Context Matters
The statement "34 of 20" inherently implies a situation where the number of favorable outcomes (34) exceeds the total number of possible outcomes (20). This is logically impossible within a single, closed event. To understand this expression, we need to consider the context.
Several interpretations are possible:
-
Cumulative Results: This is the most likely interpretation. "34 of 20" could represent accumulated results over multiple trials or events. For example:
- Sports Statistics: A basketball player might have scored 34 points across 20 games. The statistic doesn't represent a single game but an average or cumulative performance.
- Financial Markets: A trader might have made 34 successful trades out of 20 attempts over a period. This suggests a high success rate, likely involving multiple trading sessions.
- Manufacturing: A factory might have produced 34 acceptable units for every 20 units attempted, indicating a high yield rate but possibly involving multiple production runs.
-
Sampling Error or Bias: The statement could indicate a sampling error or bias. Perhaps a sample of 20 items was taken, and 34 positive instances were recorded. This might stem from:
- Incorrect Data Collection: There may have been errors in counting or recording the data.
- Biased Sampling: The sample of 20 items might not be truly representative of the entire population.
-
Theoretical Probability Exceeding 1: In some theoretical models, probabilities can exceed 1, especially when dealing with multiple dependent events or non-standard probability distributions. However, in such cases, the interpretation requires a deep understanding of the underlying model.
Calculating Relevant Probabilities and Odds
Let's assume the most likely scenario: "34 of 20" represents cumulative results. We can then calculate relevant probabilities and odds.
-
Success Rate: The success rate is simply the number of successful outcomes divided by the total number of attempts: 34/20 = 1.7. This is greater than 1, which reinforces the idea that this is a cumulative statistic across multiple events. In terms of percentage, the success rate is 170%.
-
Averaged Success Rate per Event: To get a more meaningful probability, we need to consider the average success rate per event. If we assume that each event had the same likelihood of success, we can divide the number of successful outcomes (34) by the number of events (20), resulting in an average of 1.7 successful outcomes per event. This suggests a high average success rate.
However, it's essential to remember that an average of 1.7 successful outcomes per event doesn't directly translate to a probability of 1.7, since probabilities must fall between 0 and 1.
- Interpretation using binomial distribution (if applicable): If the 20 events are independent and identically distributed Bernoulli trials (meaning each event has only two possible outcomes, success or failure), then the binomial distribution could be used to model the probability of obtaining exactly 34 successes out of 20 trials. The probability mass function would be involved, but such a probability would be extremely low (close to zero) given the disproportionate number of successes versus trials. It wouldn't be practically relevant in this context.
Real-World Examples and Applications
The concept of results exceeding the number of attempts, as illustrated by "34 of 20," appears frequently in various contexts:
-
Sports Analytics: In baseball, a batter might have accumulated 34 hits in 20 games. This high batting average, although seemingly illogical at first glance, simply represents a cumulative statistic over multiple games.
-
Investment Strategies: A hedge fund might report 34 successful investments out of 20 attempted investments. This demonstrates a high return on investment, potentially stemming from a diversified portfolio or a successful investment strategy.
-
Quality Control: In manufacturing, if 34 out of 20 tested components passed quality control, it might signal either a highly effective production process or an error in the testing procedure.
Potential Errors and Misinterpretations
It's crucial to understand the potential sources of error or misinterpretation when encountering "34 of 20" or similar statistics:
-
Data Inaccuracy: Inaccurate data collection or recording can lead to misleading results.
-
Selection Bias: The sample might not be representative of the larger population.
-
Confounding Variables: Other factors might influence the outcome, making it difficult to isolate the effect of the variable of interest.
-
Lack of Context: Without understanding the context, "34 of 20" is meaningless.
Conclusion
The seemingly contradictory phrase "34 of 20" highlights the importance of understanding the context when interpreting statistical data. While logically impossible in a single, isolated event, it often represents cumulative results across multiple trials or events. This interpretation underscores the need for careful consideration of data sources, potential biases, and the underlying processes that generate the data. Understanding probability and odds, along with a critical analysis of the context, is crucial for correctly interpreting and using such seemingly paradoxical statistics. Furthermore, it illustrates the need to always scrutinize numbers and look beyond the surface level of presented data to understand their true meaning and implications. By paying attention to detail and considering the underlying statistical framework, we can gain valuable insights and make informed decisions.
Latest Posts
Latest Posts
-
Flesh Is Grass
Sep 15, 2025
-
78 6kg In Stone
Sep 15, 2025
-
Plastic Wire Coating
Sep 15, 2025
-
North East Farming
Sep 15, 2025
-
4 Divided 3
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 34 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.