4x X 2
interactiveleap
Sep 16, 2025 · 5 min read
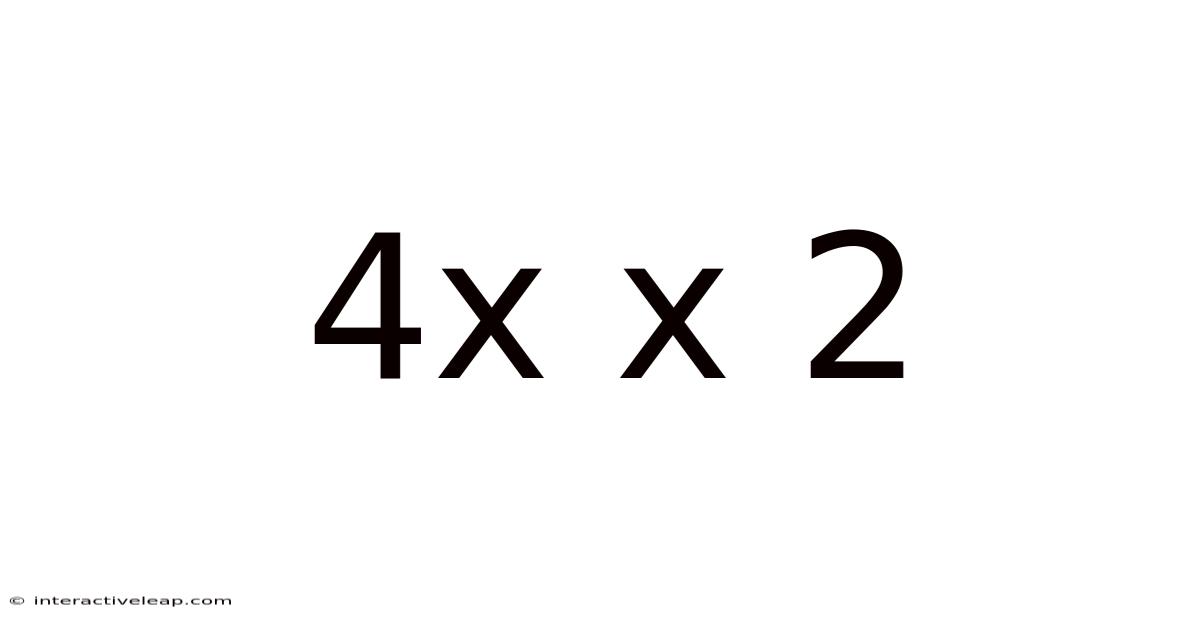
Table of Contents
Decoding 4x x 2: Exploring Multiplication, Area, and Beyond
Understanding the seemingly simple equation "4x x 2" opens doors to a world of mathematical concepts, from basic multiplication to more advanced algebraic manipulations and even real-world applications in geometry and beyond. This article delves into the intricacies of this expression, providing a comprehensive explanation suitable for learners of all levels. We will explore different interpretations, solve related problems, and even touch upon the importance of understanding the underlying principles.
Introduction: More Than Just Multiplication
At its core, "4x x 2" represents a multiplication problem. It's a concise way of expressing the repeated addition of 4x, twice. However, the presence of the variable 'x' elevates this beyond simple arithmetic; it introduces the concept of algebra and opens up possibilities for various interpretations and applications. We'll look at how to simplify this expression, its geometric representation, and its use in solving real-world problems.
Simplifying the Expression: The Power of Algebra
The most straightforward approach to simplifying "4x x 2" is to apply the commutative and associative properties of multiplication. These properties allow us to rearrange and group the terms without changing the result. Remember, the order of multiplication doesn't matter.
- Commutative Property: a x b = b x a
- Associative Property: (a x b) x c = a x (b x c)
Applying these properties, we can rewrite "4x x 2" as:
(4 x 2) x x = 8x
Therefore, the simplified form of the expression is 8x. This demonstrates a fundamental concept in algebra: combining like terms to simplify an equation.
Geometric Interpretation: Visualizing the Equation
Imagine a rectangle. Let's say the length of the rectangle is represented by '4x' and the width is 2. The area of a rectangle is calculated by multiplying its length and width. In this case, the area would be:
Area = Length x Width = 4x x 2 = 8x
This geometric representation visually reinforces the simplification process. The area of the rectangle, which is represented algebraically as 8x, is directly related to the dimensions expressed in the original equation. This connection helps to ground the abstract concept of algebraic manipulation in a concrete, visual context. Understanding this visual representation helps solidify the concept of algebraic manipulation in a relatable way, particularly for visual learners.
Solving Problems: Putting it into Practice
Let's consider some examples of how this expression might appear in real-world problems:
-
Example 1: Calculating Costs: Imagine you're buying apples. Each apple costs 'x' dollars, and you buy four bags of apples, with two apples in each bag. The total cost would be 4 x 2 x x = 8x dollars. If each apple costs $1.50 (x = 1.50), the total cost would be 8 * $1.50 = $12.
-
Example 2: Calculating Area: You're designing a rectangular garden. The length is four times the width of a smaller square flower bed (represented by 'x'), and you want to make the garden twice as wide as the flower bed. The area of the garden would be 4x x 2 = 8x. If the width of the smaller flower bed (x) is 3 meters, the area of the garden is 8 * 3 = 24 square meters.
-
Example 3: Working with Variables: Let's say you have the equation 4x x 2 = 16. To solve for x, you would first simplify the left side of the equation (as shown above): 8x = 16. Then, you divide both sides by 8 to isolate x: x = 2. This demonstrates how simplifying the expression is crucial in solving algebraic equations.
These examples show the practical applications of understanding and simplifying the equation "4x x 2." It highlights its utility in various fields requiring problem-solving and mathematical reasoning.
Exploring Further: Expanding the Concept
The simple equation "4x x 2" provides a foundation for understanding more complex algebraic manipulations. Consider the following extensions:
-
Exponents: Instead of multiplying by 2, consider raising the expression to the power of 2: (4x)² = 16x². This introduces the concept of exponents and how they affect algebraic expressions.
-
Polynomials: The expression could be part of a larger polynomial. For instance, 4x x 2 + 3x could be simplified to 11x. This introduces the concept of combining like terms within more complex algebraic expressions.
-
Equations with multiple variables: The equation could be part of a system of equations involving multiple variables, requiring the application of more advanced algebraic techniques like substitution or elimination to find solutions.
These examples highlight the building-block nature of the equation "4x x 2." Mastering the fundamentals enables understanding and tackling more complex mathematical scenarios.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 4x + 2 and 4x x 2?
- A:
4x + 2represents addition; you're adding 2 to 4x.4x x 2represents multiplication; you're multiplying 4x by 2. These are fundamentally different operations leading to different results.
- A:
-
Q: Can I always simplify expressions like this?
- A: Yes, provided you apply the rules of algebra correctly. The goal is always to combine like terms and express the equation in its simplest form.
-
Q: What if 'x' is a negative number?
- A: The same rules apply. If x = -3, for instance, then 8x = 8(-3) = -24. The result simply reflects the sign of 'x'.
-
Q: Is there a specific order of operations to follow?
- A: While the commutative and associative properties allow flexibility in the order of multiplication, the order of operations (PEMDAS/BODMAS) still holds for expressions with more than one operation. Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
-
Q: How does this relate to other mathematical concepts?
- A: This equation serves as a fundamental concept underlying many advanced mathematical concepts like calculus, linear algebra, and more complex algebraic manipulations.
Conclusion: A Foundation for Further Learning
Understanding the equation "4x x 2" is more than just mastering a simple multiplication problem. It's about grasping the fundamental principles of algebra, applying the properties of multiplication, visualizing mathematical concepts geometrically, and solving practical problems. The seemingly simple equation serves as a powerful foundation for building more sophisticated mathematical skills and understanding broader concepts within the fields of algebra, geometry, and beyond. Its simplicity belies its importance as a building block for further mathematical exploration and real-world applications. By mastering this basic concept, learners gain confidence and a solid foundation for tackling more complex mathematical challenges. The journey from understanding "4x x 2" to mastering advanced mathematical concepts is a testament to the power of building upon foundational knowledge.
Latest Posts
Latest Posts
-
85 Of 480
Sep 16, 2025
-
Factor 2x 10
Sep 16, 2025
-
2 7kg In Lbs
Sep 16, 2025
-
Man In Tophat
Sep 16, 2025
-
Micrometres To Cm
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 4x X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.