49 1 2
interactiveleap
Sep 24, 2025 · 7 min read
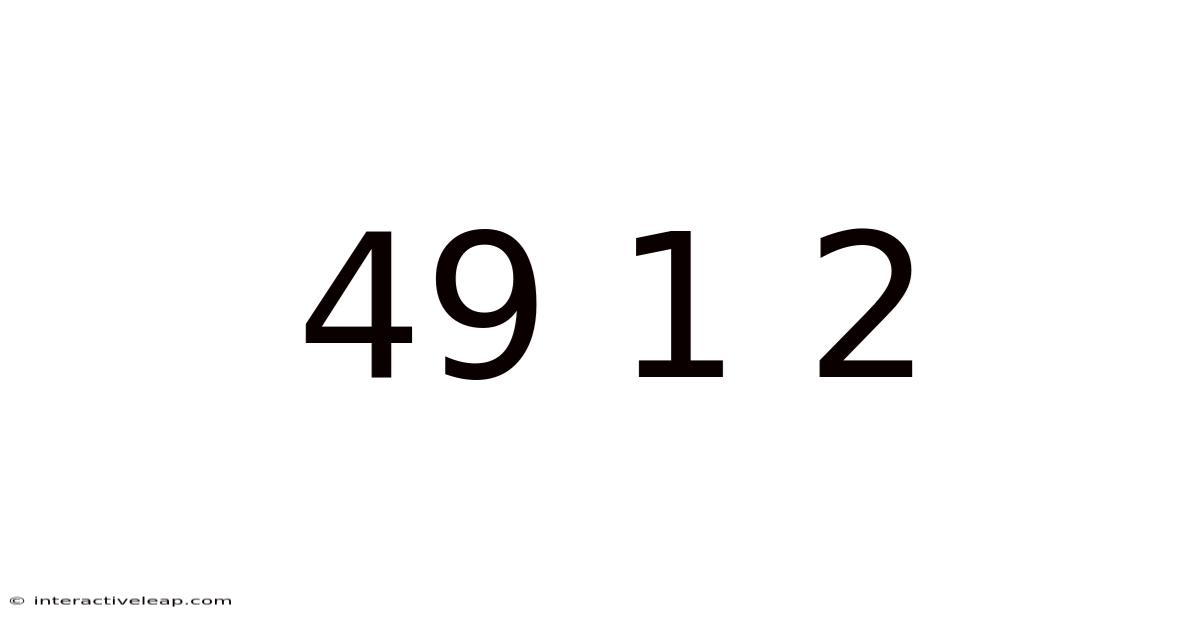
Table of Contents
Decoding 49, 1, and 2: A Journey Through Number Theory, Combinatorics, and Probability
The seemingly simple sequence "49, 1, 2" might initially appear arbitrary. However, a deeper exploration reveals a rich tapestry of mathematical connections spanning various branches of number theory, combinatorics, and probability. This article will delve into the fascinating properties of these three numbers, exploring their individual characteristics and uncovering the unexpected relationships that bind them. We'll look beyond their face value to uncover the underlying mathematical principles at play, making this journey accessible to anyone with a basic understanding of arithmetic.
I. The Individual Numbers: A Closer Look
Let's begin by examining each number individually. This initial exploration forms the foundation for understanding their more intricate interrelationships.
49: A perfect square (7²), 49 is a composite number with factors 1, 7, and 49. It holds significance in various mathematical contexts. In modular arithmetic, its properties are explored extensively. For instance, understanding its divisors is crucial in solving certain congruence equations. In geometry, 49 can represent the area of a square with side length 7. Its prime factorization (7²) is a key aspect of its number-theoretic properties.
1: The multiplicative identity, 1 is a unique number. It's neither prime nor composite, possessing only one divisor (itself). It plays a crucial role in arithmetic operations, maintaining the identity of any number it multiplies. In many mathematical structures, 1 serves as the neutral element. Its simplicity belies its fundamental importance across numerous mathematical fields.
2: The smallest prime number, 2 is the only even prime number. This seemingly simple fact has profound implications in number theory, especially in relation to Fermat's Little Theorem and other theorems about prime numbers. 2 also forms the basis of binary systems, the foundation of modern computing. Its unique property as the only even prime significantly influences the structure of prime numbers and their distribution.
II. Exploring Relationships: Combinatorics and Probability
The numbers 49, 1, and 2, while seemingly disparate, can be linked through various mathematical frameworks. Let's explore how they connect through combinatorics and probability.
Combinatorial Interpretations:
Consider the problem of arranging objects. If we have 7 distinct objects, the number of ways to arrange them in a sequence is 7! (7 factorial), which is 5040. Now, imagine we have a set of 7 distinct objects and we want to choose a subset of 2 objects. The number of ways to do this is given by the combination formula: 7C2 = 7!/(2!5!) = 21. While 49 isn't directly present in this example, it's related to the square of 7, which is the original set size. Variations of this combinatorial approach using larger sets or different subset sizes can generate relationships involving 49, or its factors, in a more direct manner.
Probabilistic Connections:
Probability often deals with ratios and fractions. Let's imagine a scenario: We have a bag containing 49 marbles, with 1 red marble and 2 blue marbles. The probability of drawing the red marble is 1/49. The probability of drawing a blue marble is 2/49. Here, we see a direct application of our numbers in a probability problem. We can extend this example to explore conditional probabilities, independent events, and other concepts in probability theory, all while using these three numbers as central components in the problem's framework. The ratios themselves highlight the fundamental principles of probability.
Further Combinatorial Explorations:
Let’s consider the concept of partitions. A partition of a positive integer n is a way of writing n as a sum of positive integers. For instance, the partitions of 4 are: 4, 3+1, 2+2, 2+1+1, 1+1+1+1. While 49 itself is a large number for manual partitioning, the concept can be applied to its smaller divisors (1 and 7). Understanding the partition function of these smaller numbers provides insight into the underlying principles that could be scaled to larger values.
The number 1, being the multiplicative identity, is a trivial case in many combinatorial problems. However, its presence often acts as a baseline or starting point for more complex calculations. The number 2, being the smallest prime, appears frequently in combinatorial problems related to binary choices or selecting subsets. It's a building block for numerous combinatorial structures.
III. Number Theory: Delving Deeper
Number theory provides a powerful lens through which to analyze the relationships between 49, 1, and 2.
Prime Factorization and Divisibility:
As previously mentioned, 49's prime factorization (7²) is crucial. This highlights the fundamental theorem of arithmetic, stating that every integer greater than 1 can be uniquely represented as a product of prime numbers. The prime factorization reveals information about divisibility rules and other number-theoretic properties. The number 1 is the only number with one divisor and forms a unique case that helps define other properties of numbers. 2, being prime, possesses only two divisors: 1 and itself. These basic divisibility properties are fundamental to more advanced number theory concepts.
Modular Arithmetic:
Modular arithmetic examines the remainders when integers are divided by a specific modulus. Considering the modulus 49, the numbers 1 and 2 have specific properties within this system. For example, understanding the multiplicative inverses of 1 and 2 (modulo 49) is relevant in solving linear congruences. These properties extend to other moduli, providing a broader understanding of how these numbers behave within different mathematical structures.
Diophantine Equations:
Diophantine equations involve finding integer solutions to polynomial equations. Simple equations involving 49, 1, and 2 might be straightforward to solve, but more complex Diophantine equations involving these numbers or their multiples can lead to challenging and insightful investigations. Exploring these equations helps us understand the nature of integer solutions and the interplay between the numbers involved.
Congruences and Residues:
The concept of congruence (a ≡ b (mod m)) is vital in number theory. Examining the congruence properties of 49, 1, and 2 modulo various integers helps us understand their behavior under different modular systems. This provides insight into their cyclical nature and their relationships within different arithmetic structures. Understanding residues – the remainders after division – is fundamental to number-theoretic analysis.
IV. Beyond the Numbers: Applications and Extensions
While we've explored mathematical properties, the numbers 49, 1, and 2 also have practical applications and can be extended into more advanced mathematical topics.
Practical Applications:
- 49: In computer science, the number 49 might relate to array sizes, memory allocation, or other computational aspects. Its square root, 7, is frequently encountered in various algorithms and data structures.
- 1: Its role as the multiplicative identity is fundamental to all arithmetic computations, making it universally relevant across various fields.
- 2: Its use in binary systems is paramount in computer science and digital electronics. Its role as the base-2 logarithm foundation is essential for numerous algorithms.
Extensions to Advanced Topics:
- Algebraic Number Theory: The properties of 49 and its prime factorization can be investigated within the context of algebraic number fields, exploring relationships between integers and algebraic numbers.
- Abstract Algebra: The number 1, as the identity element, plays a crucial role in defining groups, rings, and fields within abstract algebra. The number 2 is frequently used in examples and counter-examples to illustrate algebraic concepts.
- Cryptography: Prime numbers like 2 and the prime factors of 49 play a critical role in cryptographic algorithms, ensuring data security and encryption.
V. Conclusion: A Multifaceted Exploration
The seemingly simple sequence 49, 1, and 2 unveils a surprisingly rich mathematical landscape. By exploring their individual properties within the frameworks of number theory, combinatorics, and probability, we've uncovered numerous connections and relationships. From basic arithmetic operations to advanced concepts in abstract algebra and cryptography, these three numbers provide a foundation for understanding various mathematical principles. This exploration encourages a deeper appreciation for the interconnectedness of mathematical concepts and the surprising depth hidden within seemingly simple numerical sequences. Further investigation, perhaps focusing on specific mathematical areas, will undoubtedly uncover even more profound relationships and applications of these seemingly simple yet profoundly significant numbers.
Latest Posts
Latest Posts
-
2n 2 Sequence
Sep 24, 2025
-
85 Of 15
Sep 24, 2025
-
Dog Bows Christmas
Sep 24, 2025
-
100l In Gallons
Sep 24, 2025
-
50 In 1912
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 49 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.