85 Of 15
interactiveleap
Sep 24, 2025 · 5 min read
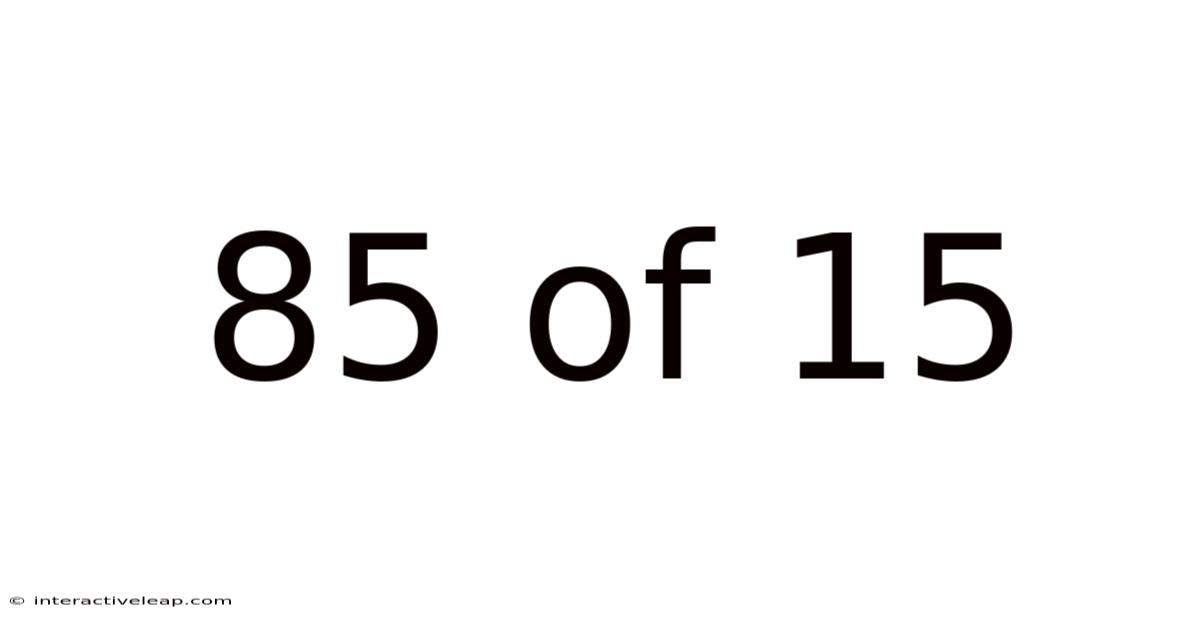
Table of Contents
Decoding 85% of 15: A Comprehensive Guide to Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to complex scientific calculations. This article delves into the seemingly simple question, "What is 85% of 15?", providing a detailed explanation of the calculation, different approaches to solving it, and exploring the broader context of percentage calculations and their real-world significance. We'll move beyond just the answer to develop a thorough understanding of the underlying principles.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" or "out of 100." This representation is incredibly useful because it provides a standardized method for comparing proportions. For example, saying that you scored 85% on a test immediately tells you that you answered 85 out of every 100 questions correctly, regardless of the actual number of questions on the test. This standardized approach is critical in various fields like finance, statistics, and science.
Calculating 85% of 15: Three Approaches
There are several ways to calculate 85% of 15. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
The most straightforward method involves converting the percentage to its decimal equivalent and then multiplying. To convert a percentage to a decimal, simply divide it by 100. In this case:
85% = 85 ÷ 100 = 0.85
Now, multiply this decimal by the number you want to find the percentage of:
0.85 x 15 = 12.75
Therefore, 85% of 15 is 12.75.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 85% can be written as 85/100. This fraction can be simplified:
85/100 = 17/20
Now, multiply this fraction by 15:
(17/20) x 15 = (17 x 15) / 20 = 255 / 20 = 12.75
Again, we arrive at the answer: 85% of 15 is 12.75.
Method 3: Using Proportion
This method relies on setting up a proportion. We know that 85% represents 85 out of 100. We can set up the following proportion:
85/100 = x/15
To solve for 'x' (which represents 85% of 15), we cross-multiply:
100x = 85 x 15
100x = 1275
x = 1275 / 100
x = 12.75
Once more, we find that 85% of 15 is 12.75.
Real-World Applications of Percentage Calculations
The ability to calculate percentages efficiently is essential in a variety of real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, and tips all involve percentage calculations. Understanding these calculations is crucial for managing personal finances effectively. For example, if a store offers a 15% discount on an item priced at $85, you would calculate 15% of $85 to determine the discount amount.
-
Statistics: Percentages are fundamental in statistical analysis. They help represent data proportions, allowing for easy comparison and interpretation of trends and patterns. For example, understanding the percentage of a population that holds a certain belief or possesses a specific characteristic is crucial in many research endeavors.
-
Science: Percentages are extensively used in scientific experiments and research to express results and error rates. For example, in calculating experimental yield or determining the percentage of a certain chemical compound in a sample.
-
Everyday Life: Percentages are encountered frequently in daily life. From understanding nutritional information on food labels (e.g., percentage of daily value for vitamins) to comprehending sale prices in stores, a solid grasp of percentages simplifies many aspects of our lives.
Beyond the Basics: More Complex Percentage Problems
While calculating 85% of 15 is relatively straightforward, percentage problems can become more complex. Here are some examples:
-
Finding the percentage: Instead of finding a percentage of a number, you might need to find what percentage one number is of another. For example, "What percentage of 20 is 5?" This requires setting up a different proportion: x/100 = 5/20.
-
Finding the original value: You may be given the percentage and the resulting value and need to find the original value. For example, "If 25% of a number is 10, what is the number?" This requires some algebraic manipulation.
-
Percentage increase/decrease: This involves calculating the percentage change between two values. For example, if a price increases from $10 to $15, what is the percentage increase? This requires calculating the difference between the two values, dividing that difference by the original value, and then multiplying by 100.
Mastering these more complex variations expands the practical application of percentage calculations.
Frequently Asked Questions (FAQ)
-
Q: Why are percentages so important?
A: Percentages provide a standardized way to express proportions, making comparisons easy and facilitating better understanding across different contexts. They simplify complex information into easily digestible formats.
-
Q: What if I need to calculate a percentage that isn't a whole number?
A: The methods described above work equally well with decimal percentages. For example, to find 12.5% of 20, you would convert 12.5% to 0.125 and multiply by 20.
-
Q: Are there any tools to help calculate percentages?
A: Yes, many online calculators and spreadsheet software (like Microsoft Excel or Google Sheets) provide built-in functions for percentage calculations. These can be very helpful for complex or repetitive calculations.
-
Q: How can I improve my understanding of percentages?
A: Practice is key! Try working through various percentage problems, starting with simple examples and gradually progressing to more complex ones. Focusing on understanding the underlying principles, rather than just memorizing formulas, will improve long-term comprehension.
Conclusion: Mastering the Power of Percentages
This in-depth exploration of calculating 85% of 15 has moved beyond a simple answer to highlight the broader importance of understanding percentages. From the simplicity of finding a percentage of a number to the more advanced applications in finance, statistics, and various other fields, the skill of calculating and interpreting percentages remains invaluable. By mastering these fundamental concepts, you equip yourself with a powerful tool applicable to a wide range of situations, enhancing both your problem-solving abilities and your understanding of the world around you. Consistent practice and a focus on the underlying principles will solidify your understanding and make percentage calculations second nature. Remember, the key lies not just in getting the right answer, but in understanding why that answer is correct.
Latest Posts
Latest Posts
-
8 Of 50
Sep 24, 2025
-
98 7 Fahrenheit Celsius
Sep 24, 2025
-
Complement Fixation Test
Sep 24, 2025
-
40ml To Tbsp
Sep 24, 2025
-
15 Of 99
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 85 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.