4 X 36
interactiveleap
Sep 25, 2025 · 6 min read
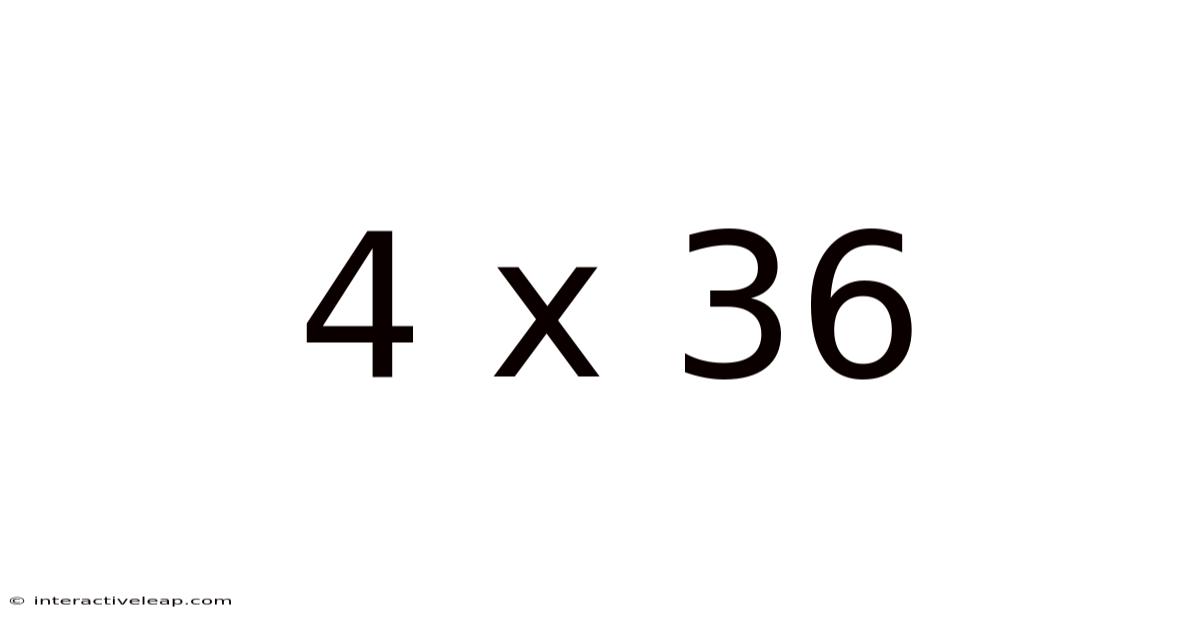
Table of Contents
Decoding 4 x 36: A Deep Dive into Multiplication, Its Applications, and Beyond
This article explores the seemingly simple calculation of 4 x 36, delving beyond the immediate answer to uncover the fundamental principles of multiplication, its diverse applications in various fields, and its connection to broader mathematical concepts. We’ll examine different methods of solving this problem, discuss its real-world relevance, and even touch upon the historical context of multiplication. Understanding 4 x 36 is not just about finding the product; it's about grasping the power and versatility of this core mathematical operation.
Introduction: More Than Just a Calculation
The multiplication problem 4 x 36 might seem trivial at first glance. The answer, 144, is easily obtained with a calculator or basic multiplication knowledge. However, exploring this seemingly simple equation reveals a wealth of mathematical concepts and real-world applications. This article will unpack the various ways to solve 4 x 36, demonstrating the underlying principles and showing how this basic calculation forms the foundation for more complex mathematical operations and problem-solving. We will discuss the importance of understanding multiplication beyond rote memorization and highlight its relevance in various fields like engineering, finance, and everyday life.
Methods for Solving 4 x 36
There are several ways to solve 4 x 36, each illustrating different mathematical concepts:
-
Standard Multiplication: This is the most common method, involving multiplying the units digit first, then the tens digit, and finally adding the results.
- 36 x 4 = (4 x 6) + (4 x 30) = 24 + 120 = 144
-
Distributive Property: This method leverages the distributive property of multiplication over addition. We can break down 36 into 30 + 6, making the calculation easier:
- 4 x (30 + 6) = (4 x 30) + (4 x 6) = 120 + 24 = 144
-
Repeated Addition: Multiplication is essentially repeated addition. This approach is particularly useful for visualizing the concept of multiplication, especially for younger learners:
- 36 + 36 + 36 + 36 = 144
-
Using Arrays: Visual learners might find representing the problem using an array helpful. This involves arranging objects in rows and columns. A 4 x 36 array would consist of 4 rows with 36 objects in each row. Counting all the objects yields the answer, 144.
-
Mental Math Techniques: With practice, one can develop mental math techniques to quickly solve this. For example, doubling: 36 x 2 = 72, then doubling again: 72 x 2 = 144.
The Significance of Multiplication: Beyond the Numbers
The seemingly simple act of multiplying 4 by 36 underlies many complex systems and processes. Let’s explore some key areas:
-
Engineering and Physics: Multiplication is fundamental to many engineering and physics calculations. From determining the area of a rectangle (length x width) to calculating forces, velocities, and accelerations, multiplication is essential for accurate computations and design. Consider calculating the total weight of 36 identical components each weighing 4 kg – the answer, 144 kg, is crucial for structural design.
-
Finance and Business: Multiplication is essential in numerous financial calculations. Calculating total cost (quantity x price), interest earned, or profit margins all rely heavily on multiplication. For instance, if a company sells 36 units of a product at $4 per unit, their revenue is calculated as 36 x $4 = $144.
-
Everyday Life: Multiplication is ubiquitous in daily life. From calculating the total cost of groceries, determining the amount of ingredients needed for a recipe (multiplying ingredient quantities), to figuring out how many tiles are needed to cover a floor, multiplication simplifies many everyday tasks.
-
Computer Science: Multiplication is a fundamental operation in computer science, forming the basis of various algorithms and calculations. From simple arithmetic to complex matrix operations, multiplication plays a crucial role in computer processing.
Expanding the Concept: Exploring Related Mathematical Ideas
Understanding 4 x 36 opens doors to a wider understanding of several mathematical concepts:
-
Factors and Multiples: 4 and 36 are factors of 144. 144 is a multiple of both 4 and 36. Exploring factors and multiples expands the understanding of number relationships and divisibility rules.
-
Prime Factorization: Breaking down a number into its prime factors is a crucial concept in number theory. The prime factorization of 144 is 2⁴ x 3². This reveals the fundamental building blocks of the number 144.
-
Exponents and Powers: The prime factorization of 144 shows the use of exponents (2⁴ and 3²). Understanding exponents allows us to represent large numbers in a more compact and manageable form.
-
Algebra: The concept of multiplication extends naturally into algebra, where variables replace numbers. For example, 4x = 144 can be solved to find the value of x (x = 36).
-
Geometry: Multiplication is crucial in geometric calculations. Calculating the area of rectangles, volumes of cubes and rectangular prisms, and the circumference of circles all require multiplication. The area of a rectangle with sides 4 and 36 is, of course, 144 square units.
Historical Context: The Evolution of Multiplication
Multiplication, like other fundamental mathematical concepts, has evolved over centuries. Early civilizations developed various methods for multiplication, some of which involved using different tools and techniques. From using fingers for simple calculations to employing sophisticated abaci and eventually written algorithms, the evolution of multiplication reflects the progress of mathematical understanding and technology. Understanding this history provides valuable insights into the development of mathematical thought.
Frequently Asked Questions (FAQ)
-
What are some real-world examples of using 4 x 36? Calculating the total cost of 36 items costing $4 each; determining the total weight of 36 objects weighing 4 kg each; figuring out the number of square tiles needed to cover a 4 x 36 ft area.
-
How can I improve my multiplication skills? Practice regularly using different methods, use flashcards, play multiplication games, and try to solve problems mentally.
-
What are some common mistakes when multiplying? Errors in carrying over numbers, misplacing digits, and neglecting to consider place values are common pitfalls.
-
Is there a faster way to solve 4 x 36 than standard multiplication? Yes, using the distributive property or mental math techniques (like doubling) can be faster.
Conclusion: Unlocking the Power of 4 x 36
The simple equation 4 x 36, while seemingly straightforward, serves as a gateway to a vast landscape of mathematical concepts and their applications. By exploring its various solutions, understanding its real-world relevance, and delving into related mathematical ideas, we gain a deeper appreciation for the power and versatility of multiplication. It's not merely about getting the answer (144); it's about grasping the fundamental principles that underpin much of our understanding of the world around us. The journey from a basic calculation to a comprehensive understanding of multiplication showcases the beauty and elegance of mathematics, highlighting its importance in shaping our world. Further exploration of these concepts will undoubtedly enhance your mathematical skills and broaden your understanding of this crucial element of arithmetic.
Latest Posts
Latest Posts
-
63kgs In Stone
Sep 25, 2025
-
0 17 In Fraction
Sep 25, 2025
-
5x 6 3x
Sep 25, 2025
-
20 Of 230000
Sep 25, 2025
-
185g In Oz
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 4 X 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.