20 Of 230000
interactiveleap
Sep 25, 2025 · 6 min read
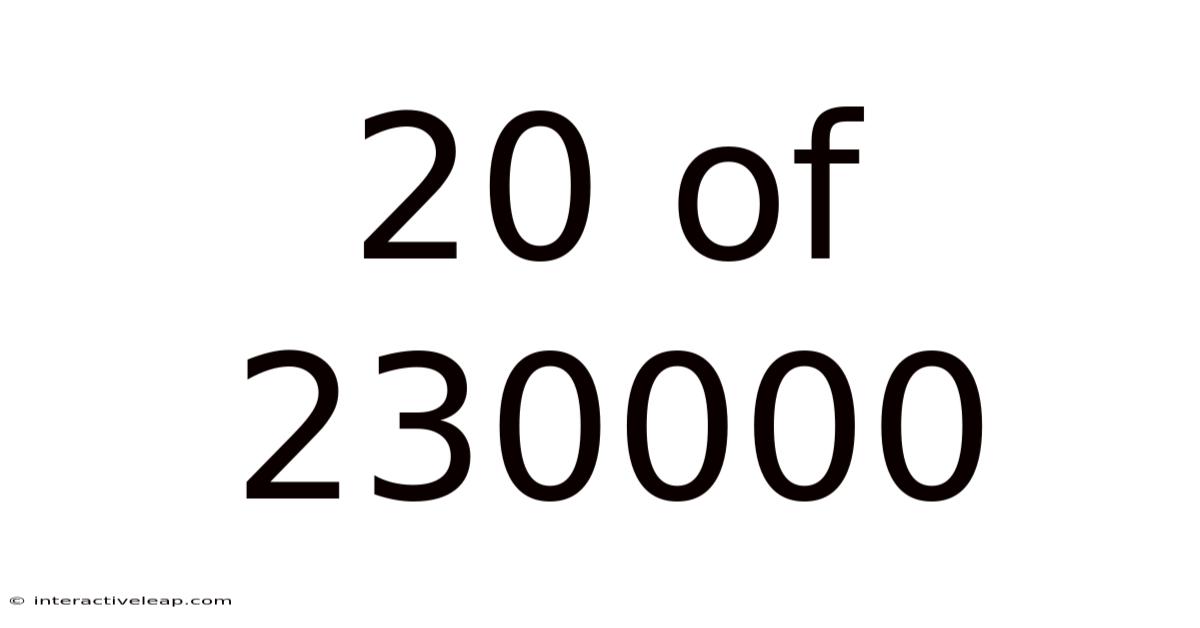
Table of Contents
20 out of 230,000: Understanding Statistical Significance and Its Real-World Applications
Understanding the meaning of "20 out of 230,000" requires more than just simple division. This seemingly small fraction represents a statistical event, and its significance depends entirely on the context. This article delves into interpreting such ratios, exploring the concepts of probability, statistical significance, and how we apply this understanding to various real-world scenarios, from medical trials to quality control in manufacturing. We'll unravel the nuances behind seemingly insignificant numbers and demonstrate how they can hold significant weight in decision-making processes.
Understanding the Basics: Probability and Ratios
At its core, "20 out of 230,000" is a ratio expressing a proportion. Simple division reveals that this represents approximately 0.0087%, or 8.7 parts per 10,000. While this number seems small, its significance is heavily reliant on the underlying context. Is this ratio describing the defect rate in a manufacturing process? The prevalence of a rare disease? The success rate of a new treatment?
The field of probability helps us understand the likelihood of events occurring. In the case of "20 out of 230,000," we could ask: what is the probability of observing 20 occurrences given a total of 230,000 trials? This question leads us into the realm of statistical hypothesis testing.
Statistical Significance: Is 20 out of 230,000 Meaningful?
Statistical significance assesses whether an observed result is likely due to chance or reflects a real effect. It's crucial to remember that a statistically significant result doesn't necessarily mean the effect is large or practically important; it simply means it's unlikely to have occurred randomly.
Determining significance involves several factors:
-
The Null Hypothesis: This is the default assumption—in this case, it might be that there's no real difference or effect. For example, the null hypothesis could be that the defect rate is 0%.
-
The Alternative Hypothesis: This is the claim we're trying to support. We might hypothesize that the defect rate is greater than 0%, or that a specific treatment is effective.
-
The Significance Level (alpha): This is a pre-determined threshold, usually 0.05 (5%). If the probability of observing the results (or more extreme results) under the null hypothesis is less than alpha, we reject the null hypothesis and consider the result statistically significant. This means there's less than a 5% chance the results occurred by random chance.
-
P-value: The p-value represents the probability of observing the results (or more extreme results) if the null hypothesis were true. A p-value less than alpha (e.g., 0.05) indicates statistical significance.
Determining the p-value for "20 out of 230,000" requires specific statistical tests, such as a binomial test or a Poisson test, depending on the underlying assumptions about the data.
Real-World Applications: Interpreting 20 out of 230,000 in Different Contexts
The interpretation of "20 out of 230,000" dramatically varies depending on the context:
1. Medical Research:
Imagine 20 out of 230,000 participants in a clinical trial experienced a serious adverse event after receiving a new drug. While the rate is low (0.0087%), the absolute number of adverse events could be concerning. The statistical significance would depend on the expected adverse event rate for similar drugs. If the expected rate is significantly lower, the observed 20 cases might be statistically significant, suggesting the new drug carries an increased risk. Further investigation would be necessary.
2. Manufacturing Quality Control:
In a manufacturing setting, 20 defective items out of 230,000 produced might be unacceptable, even if statistically insignificant. The cost of replacing or repairing these 20 items, along with the potential loss of customer trust, might outweigh the statistical insignificance. Quality control focuses on minimizing defects, regardless of statistical significance levels.
3. Environmental Monitoring:
If 20 out of 230,000 water samples tested positive for a specific contaminant, this could indicate a localized pollution event or a problem with the testing methodology. While the rate is low, the context demands further investigation to identify the source and prevent future contamination.
4. Rare Disease Prevalence:
20 confirmed cases of a rare genetic disorder among 230,000 individuals might provide valuable data for epidemiological studies. While seemingly small, this data point contributes to a larger understanding of disease prevalence and distribution within a population.
The Importance of Context and Further Analysis
The interpretation of "20 out of 230,000" isn't solely determined by statistical significance. Other factors play a crucial role:
-
The Cost of Error: The consequences of being wrong—either falsely rejecting the null hypothesis (Type I error) or failing to reject a false null hypothesis (Type II error)—must be considered.
-
Practical Significance: Even if statistically significant, the effect might be too small to be practically relevant. For example, a slightly improved treatment with a statistically significant but minuscule effect on patient outcomes might not be worth the added cost or complexity.
-
Underlying Assumptions: The validity of statistical inferences depends on the assumptions made about the data. Violating these assumptions can lead to inaccurate conclusions.
-
Sample Size: The larger the sample size (230,000 in this case), the more likely it is to detect even small effects. A smaller sample size might obscure a real effect, while a larger sample size might highlight a statistically significant but practically insignificant effect.
-
Data Quality: The accuracy and reliability of the data are paramount. Errors in data collection or measurement can significantly impact the interpretation of results.
Further Statistical Considerations
Beyond simply determining significance, several other statistical concepts could enhance our understanding of "20 out of 230,000":
-
Confidence Intervals: These provide a range of plausible values for the true proportion within the population. A 95% confidence interval, for instance, would give a range of values that we're 95% confident contains the true proportion.
-
Bayesian Statistics: This approach incorporates prior knowledge or beliefs into the analysis, providing a more nuanced interpretation, especially when dealing with rare events.
-
Power Analysis: This technique helps determine the sample size required to detect a specific effect with a desired level of power (the probability of correctly rejecting a false null hypothesis).
Frequently Asked Questions (FAQ)
Q: How do I calculate the p-value for "20 out of 230,000"?
A: The exact calculation depends on the underlying assumptions about the data. A binomial test is suitable if we're dealing with a fixed number of trials (230,000) and a binary outcome (defective/non-defective). A Poisson test might be more appropriate if we're modeling the occurrence of rare events. Statistical software packages or online calculators can perform these calculations.
Q: Is a statistically significant result always practically significant?
A: No. Statistical significance indicates an effect is unlikely due to chance, but it doesn't necessarily mean the effect is large or meaningful in the real world. Consider the context and cost-benefit implications.
Q: What if my sample size is smaller?
A: With a smaller sample size, it becomes more difficult to detect statistically significant differences, even if a real effect exists. This can lead to Type II errors (failing to reject a false null hypothesis).
Conclusion: The Contextual Importance of Statistical Analysis
The interpretation of "20 out of 230,000" is far from straightforward. It's not simply a matter of calculating a percentage; it requires a deep understanding of statistical principles, context, and potential biases. This seemingly small fraction can hold significant weight depending on the application, underscoring the necessity of rigorous statistical analysis in drawing meaningful conclusions from data. Remember to always consider the broader context, potential errors, and the practical implications of any statistical findings before reaching a conclusion. A robust analysis considers not only the numbers but also the underlying story they tell.
Latest Posts
Latest Posts
-
Disintegrations Per Minute
Sep 25, 2025
-
8 15 Simplified
Sep 25, 2025
-
9 15 Simplified
Sep 25, 2025
-
Mole To Millimole
Sep 25, 2025
-
Poet Liz Berry
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 230000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.