3x X 2
interactiveleap
Sep 16, 2025 · 5 min read
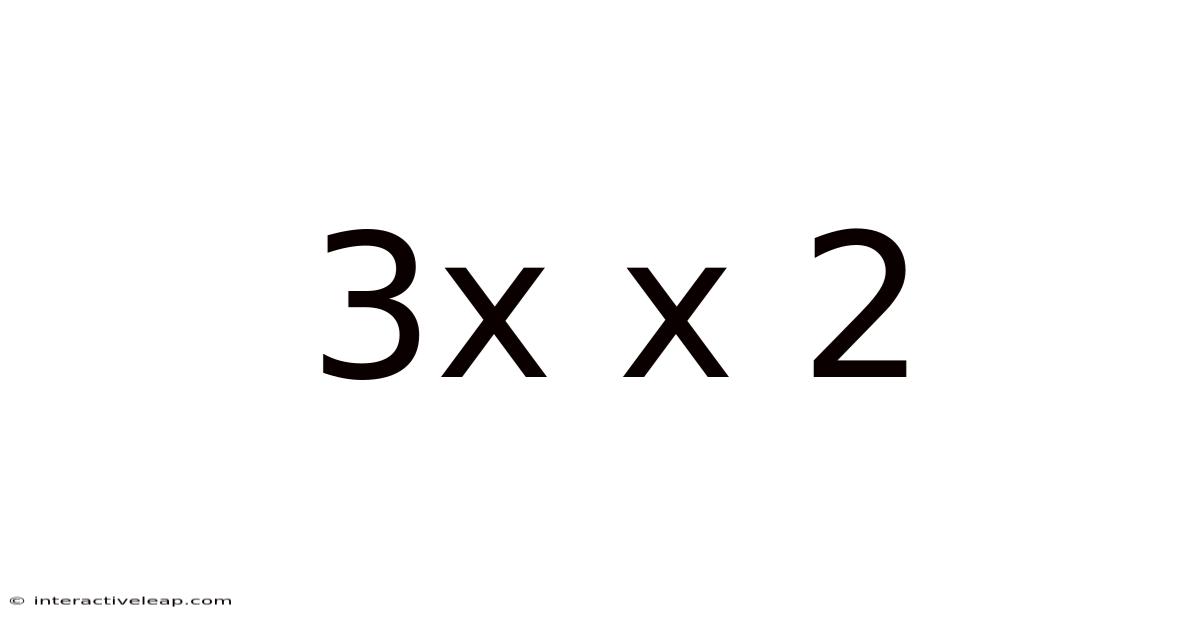
Table of Contents
Decoding 3x x 2: Exploring Multiplication, Algebra, and Beyond
This article delves into the seemingly simple mathematical expression "3x x 2," unpacking its meaning, exploring its applications in various mathematical contexts, and highlighting its significance in building a strong foundation in algebra and beyond. We'll move beyond simply calculating the result to understand the underlying principles and the broader implications of this expression. This exploration will be beneficial for students of all levels, from those just grasping the basics of multiplication to those tackling more advanced algebraic concepts.
Introduction: Understanding the Fundamentals
At its core, "3x x 2" represents a multiplication problem. The 'x' in this case acts as a variable, representing an unknown quantity or a placeholder for a number. Understanding this distinction is crucial. Unlike a simple arithmetic problem like 3 x 2 = 6, where we are dealing with known constants, "3x x 2" introduces an element of abstraction. The expression implies the multiplication of three times an unknown value ('x') and then further multiplying the result by 2.
Step-by-Step Calculation and Simplification
Let's break down the calculation process:
-
Multiplication of Coefficients: First, we multiply the known numerical coefficients: 3 and 2. This gives us 6.
-
Combining with the Variable: The variable 'x' remains unchanged throughout this step. It essentially 'tags along' with the result of the coefficient multiplication.
-
Simplified Expression: The simplified expression becomes 6x. This means that whatever value 'x' represents, the final result will be six times that value.
Therefore, 3x x 2 = 6x. This simplification is a fundamental concept in algebra, demonstrating the power of combining like terms to make expressions more manageable and easier to interpret.
Illustrative Examples: Bringing it to Life
Let's illustrate the concept with a few practical examples:
-
Example 1: Imagine 'x' represents the number of apples in a basket. If you have three baskets, each containing 'x' apples, and you double the total number of apples, you will have 6x apples. If each basket contains 5 apples (x=5), then you'll have 6 * 5 = 30 apples.
-
Example 2: Let's say 'x' represents the cost of a single pen. If you buy three pens and then buy another set of three pens, you've essentially purchased 6 pens (3 pens + 3 pens). Thus, the total cost would be 6x. If each pen costs $2 (x=2), the total cost would be 6 * $2 = $12.
-
Example 3: Suppose 'x' represents the side length of a square. The area of the square would be x². If you have three such squares and double the total area, the resulting area is represented as 3x² x 2 = 6x². If x = 4 cm (side length of one square), then the total area would be 6 * (4 cm)² = 6 * 16 cm² = 96 cm².
These examples showcase the practical applicability of the expression "3x x 2" in various real-world scenarios, demonstrating its relevance beyond abstract mathematical concepts.
Algebraic Applications: Expanding the Scope
The expression "3x x 2 = 6x" is fundamental to many algebraic manipulations and problem-solving techniques. It underpins several key concepts:
-
Distributive Property: This principle states that a(b + c) = ab + ac. While not directly apparent in "3x x 2," understanding this property is essential for solving more complex equations involving variables. For instance, 2(3x + 5) = 6x + 10 demonstrates the application of the distributive property.
-
Solving Equations: This expression helps in solving linear equations. For example, if 6x = 12, we can find the value of 'x' by dividing both sides by 6, resulting in x = 2. This simple equation demonstrates how the simplified expression simplifies the problem solving.
-
Simplifying Expressions: In more complex algebraic expressions, this simplification is crucial. Consider the expression: 5x + 3x x 2 - 4x. Simplifying this would require understanding the order of operations (PEMDAS/BODMAS) and the multiplication of the '3x' and '2' (resulting in '6x'), leading to 5x + 6x - 4x = 7x.
Advanced Concepts: Beyond the Basics
The understanding of "3x x 2 = 6x" is a stepping stone to more advanced mathematical concepts:
-
Polynomials: This expression is a simple example of a polynomial (a mathematical expression involving variables and coefficients). More complex polynomials can involve higher powers of 'x' (e.g., x², x³, etc.) and multiple terms.
-
Calculus: In calculus, understanding variable manipulation and simplification is critical for tasks like differentiation and integration. The simplification we performed here is a fundamental building block for these advanced operations.
-
Linear Algebra: The concept of scalar multiplication (multiplying a vector or matrix by a constant) in linear algebra is directly related to this principle.
Frequently Asked Questions (FAQ)
-
Q: What if 'x' is a negative number? A: The process remains the same. The result will still be 6x. For example, if x = -3, then 6x = 6(-3) = -18.
-
Q: Can 'x' represent any value? A: Yes, 'x' can represent any real number (positive, negative, or zero).
-
Q: What is the difference between 3x x 2 and 3 x 2x? A: There is no difference. Multiplication is commutative, meaning the order of the operands does not affect the result. Both expressions simplify to 6x.
-
Q: Is it always necessary to simplify the expression to 6x? A: While simplifying is often beneficial for clarity and solving equations, it is not always mandatory. The original expression "3x x 2" is mathematically correct, but 6x is more concise and often more convenient to work with.
Conclusion: A Cornerstone of Mathematical Understanding
The seemingly simple expression "3x x 2" holds a significant position in the world of mathematics. Its understanding is fundamental to mastering basic algebra and serves as a crucial stepping stone towards more complex mathematical concepts. From solving simple equations to tackling advanced problems in calculus and linear algebra, the principle of simplifying expressions involving variables is consistently utilized. By grasping the core principles discussed here, students will build a stronger mathematical foundation and enhance their ability to solve a wide range of problems across various fields of study. The simplicity of this expression belies its profound impact on mathematical understanding and problem-solving capabilities. Mastering this seemingly basic concept opens doors to a deeper appreciation and comprehension of the beauty and power of mathematics.
Latest Posts
Latest Posts
-
85 Of 480
Sep 16, 2025
-
Factor 2x 10
Sep 16, 2025
-
2 7kg In Lbs
Sep 16, 2025
-
Man In Tophat
Sep 16, 2025
-
Micrometres To Cm
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 3x X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.