35 Of 90
interactiveleap
Sep 21, 2025 · 5 min read
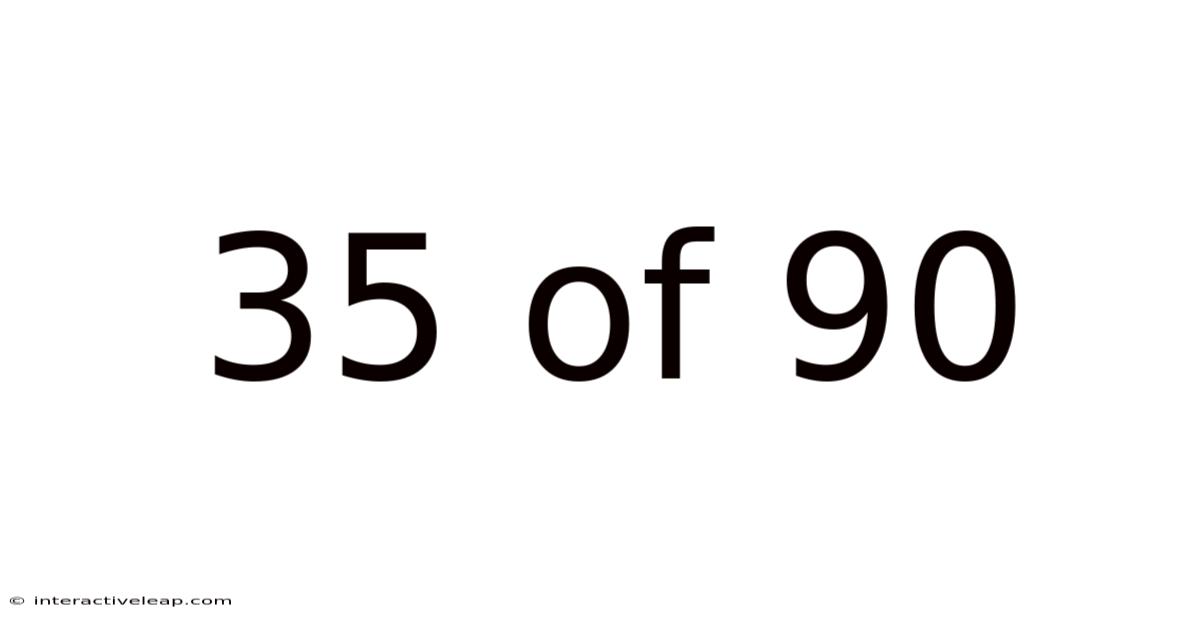
Table of Contents
Decoding the Fraction: Understanding 35/90 and its Implications
The seemingly simple fraction 35/90 might appear insignificant at first glance. However, understanding this fraction, simplifying it, and exploring its implications within various mathematical contexts reveals a surprising depth. This article delves into the intricacies of 35/90, exploring its simplification, decimal representation, percentage equivalent, and practical applications, all while maintaining a clear, engaging, and educational tone accessible to a broad audience. We'll unpack its meaning, explore its uses in different scenarios, and finally, address some frequently asked questions.
Introduction to 35/90
The fraction 35/90 represents a part-to-whole relationship. It indicates that we have 35 parts out of a total of 90 parts. This can represent many real-world scenarios, from the proportion of students who passed a test to the percentage of a task completed. Before exploring its various interpretations, let’s start with the most fundamental step: simplification.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
The key to understanding 35/90 more effectively is to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of both the numerator (35) and the denominator (90) and dividing both by that number.
The prime factorization method is a reliable way to find the GCD. Let's break down 35 and 90 into their prime factors:
- 35 = 5 x 7
- 90 = 2 x 3 x 3 x 5
The common prime factor is 5. Therefore, the GCD of 35 and 90 is 5.
Dividing both the numerator and denominator by 5, we get:
35 ÷ 5 = 7 90 ÷ 5 = 18
Therefore, the simplified form of 35/90 is 7/18. This simplified fraction is easier to work with and provides a clearer representation of the proportion.
Decimal Representation and Percentage Equivalent
Converting the fraction 7/18 into a decimal involves dividing the numerator (7) by the denominator (18):
7 ÷ 18 ≈ 0.3888...
This is a recurring decimal, meaning the digit 8 repeats infinitely. For practical purposes, we can round it to a specific number of decimal places, for example, 0.39.
To convert the decimal to a percentage, we multiply by 100:
0.3888... x 100 ≈ 38.89%
Therefore, 35/90, simplified to 7/18, is approximately equal to 0.39 or 38.89%.
Practical Applications of 35/90 (or 7/18)
The fraction 35/90, or its simplified equivalent 7/18, can be applied in a multitude of real-world scenarios. Consider these examples:
- Test Scores: If a student answered 35 questions correctly out of a total of 90 questions, their score would be 35/90, or 38.89%.
- Project Completion: If 35 out of 90 tasks in a project are completed, the project's completion rate is 38.89%.
- Survey Results: If 35 out of 90 respondents answered "yes" to a particular question in a survey, the proportion of "yes" responses is 38.89%.
- Sales Figures: If a company sold 35 units of a product out of a total of 90 units produced, the sales rate is 38.89%.
- Recipe Ratios: In baking or cooking, the fraction could represent the ratio of ingredients. For example, 7 parts flour to 18 parts water.
Further Mathematical Explorations
Beyond its simple representation, 35/90 opens doors to further mathematical explorations:
- Ratio and Proportion: The fraction establishes a ratio between two quantities, enabling us to solve problems involving proportional relationships. For instance, if 7 out of 18 students prefer a certain activity, we can use this ratio to predict the number of students who might prefer it in a larger group.
- Probability: In probability, 7/18 could represent the probability of a specific event occurring. For example, if there are 18 equally likely outcomes, and 7 of them are favorable, the probability of the favorable outcome is 7/18.
- Algebra: Fractions like 7/18 can be used in algebraic equations, requiring operations such as addition, subtraction, multiplication, and division involving fractions.
Comparing Fractions: 35/90 in Context
To better understand the magnitude of 35/90 (or 7/18), let's compare it to other fractions:
- 1/2 (50%): 7/18 is less than 1/2, meaning it represents a proportion less than half.
- 1/3 (33.33%): 7/18 is slightly greater than 1/3, indicating a proportion just above one-third.
- 1/4 (25%): 7/18 is significantly larger than 1/4.
These comparisons help contextualize the size and value of the fraction.
Addressing Common Questions (FAQ)
Here are some frequently asked questions regarding fractions like 35/90:
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand and work with. It provides a more concise and efficient representation of the proportion. It also helps in comparing fractions and performing calculations more easily.
Q2: What if I get a different simplified fraction?
A2: If you obtain a different simplified fraction, double-check your calculations. Make sure you have found the greatest common divisor. If you divide by a common factor that isn't the greatest, you won't get the simplest form of the fraction.
Q3: Can I use a calculator to simplify fractions?
A3: Many calculators have a function to simplify fractions. However, understanding the manual process of finding the GCD is crucial for a deeper understanding of the underlying mathematical principles.
Q4: What are some real-world applications beyond those mentioned?
A4: The applications are virtually limitless. Any scenario involving parts of a whole, ratios, proportions, or probabilities can potentially utilize fractions like 35/90. Think about mixing paints, calculating discounts, or analyzing statistical data.
Conclusion: The Significance of Understanding Fractions
Understanding fractions like 35/90 is essential for navigating various aspects of mathematics and real-world problem-solving. By mastering the simplification process, converting to decimals and percentages, and applying these concepts to different contexts, you gain a powerful tool for interpreting data, solving problems, and making informed decisions. The seemingly simple 35/90, when explored in depth, unveils a richness that extends far beyond its initial appearance. Remember, the key is to break down the problem, apply the fundamental principles, and appreciate the practical implications of this mathematical concept.
Latest Posts
Latest Posts
-
Mr Of Butanol
Sep 21, 2025
-
25 Of 21
Sep 21, 2025
-
58cm To Inches
Sep 21, 2025
-
25 Of 80000
Sep 21, 2025
-
0 4 Liters Milliliters
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 35 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.