25 Of 80000
interactiveleap
Sep 21, 2025 · 6 min read
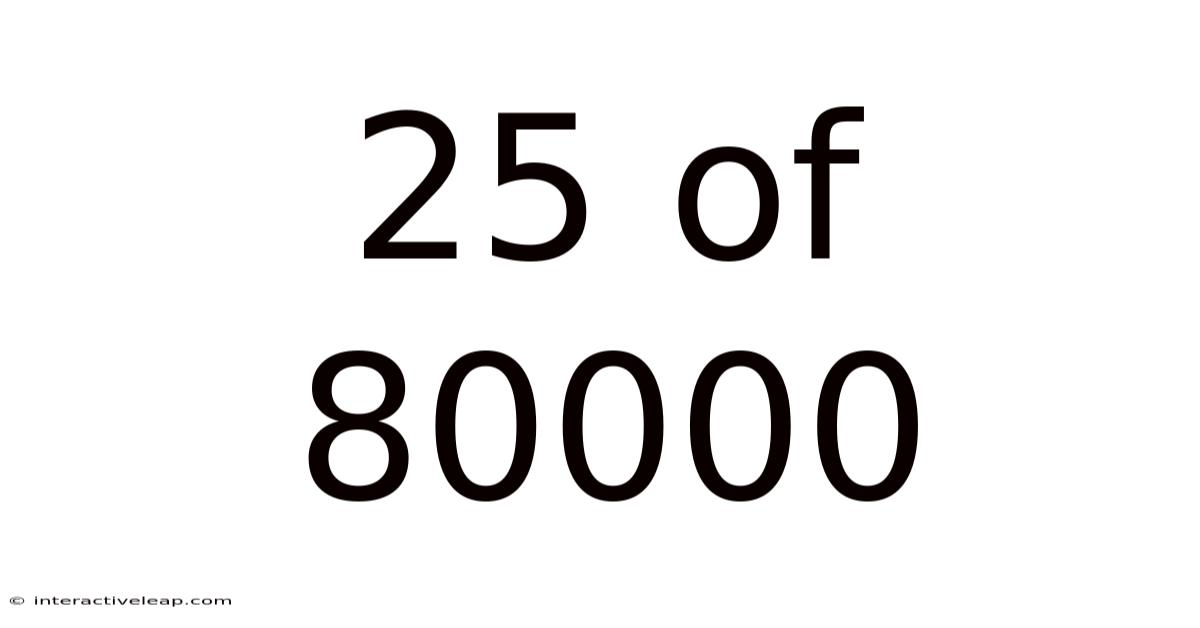
Table of Contents
Unveiling the Significance of 25 out of 80,000: A Deep Dive into Probability, Statistics, and Real-World Applications
The seemingly small fraction, 25 out of 80,000, might appear insignificant at first glance. However, understanding its implications requires delving into the realm of probability, statistics, and their diverse applications in various fields. This article explores the meaning of this fraction, its mathematical representation, its statistical significance, and how such data points are interpreted and applied in real-world scenarios. We'll move beyond simple calculation to grasp the underlying principles and potential impact of such data.
Understanding the Basics: Probability and Proportion
Before diving into the intricacies of 25 out of 80,000, let's establish a fundamental understanding of probability and proportion. Probability measures the likelihood of an event occurring. It's expressed as a number between 0 and 1, where 0 indicates impossibility and 1 indicates certainty. A proportion, on the other hand, represents the ratio of a part to the whole. In our case, 25 represents the "part" and 80,000 represents the "whole."
The proportion 25/80,000 can be easily calculated:
25 ÷ 80,000 = 0.0003125
This means that the proportion is 0.0003125 or 0.03125%. This is a very small proportion. However, the significance of this proportion depends entirely on the context in which it's presented. A small proportion in one situation might be highly significant in another.
Calculating Percentage and Rates
Expressing 25 out of 80,000 as a percentage provides a more intuitive understanding:
(25/80,000) * 100% = 0.03125%
This signifies that 25 represents approximately 0.03125% of the total 80,000.
Understanding rates, which represent the frequency of an event over time, adds another layer of interpretation. For example, if these numbers represent occurrences over a year, the rate would be extremely low. However, if the timeframe is significantly shorter, the rate could be considered substantial. Context is key.
Statistical Significance and Hypothesis Testing
The statistical significance of 25 out of 80,000 depends heavily on the context. To determine its significance, we would typically employ hypothesis testing. This involves formulating a null hypothesis (e.g., there is no significant difference between the observed proportion and an expected proportion) and an alternative hypothesis (e.g., there is a significant difference).
We would then use statistical tests, such as a z-test or chi-square test, to determine the probability of observing the data (25 out of 80,000) if the null hypothesis were true. If this probability (p-value) is below a predetermined significance level (typically 0.05), we would reject the null hypothesis and conclude that the observed proportion is statistically significant.
Interpreting the Data: Context Matters
The interpretation of 25 out of 80,000 varies dramatically depending on the context. Let's consider several scenarios:
-
Medical Research: If 25 out of 80,000 patients experienced a serious adverse reaction to a new drug, this would likely be considered a low but potentially significant adverse event rate, especially when compared to the expected rate of such events in the control group and considering the severity of the reactions. Further investigation would be crucial to determine causality and the overall safety profile of the drug. Even small percentages can have serious implications when concerning human health.
-
Manufacturing Defects: If 25 out of 80,000 manufactured products were defective, the defect rate would be considered relatively low for many industries. However, the cost associated with recalling and repairing those defects, coupled with potential damage to brand reputation, must be carefully weighed against the cost of enhanced quality control.
-
Election Results: In a close election, 25 out of 80,000 votes might represent a crucial margin of victory or defeat. In this situation, every single vote matters.
-
Environmental Studies: If 25 out of 80,000 samples of water tested positive for a specific pollutant, that could signal a potential environmental problem requiring investigation.
-
Social Science Research: In a survey of 80,000 people, 25 responses indicating a particular opinion might be considered statistically insignificant, but that depends on the expected proportion and the margin of error within the sample.
Real-World Applications and Case Studies
The application of proportions and statistical analysis extends far beyond these examples. Several fields rely heavily on the interpretation of such data:
-
Epidemiology: Epidemiologists study the distribution and determinants of health-related states or events in specified populations, often using proportional data to understand disease prevalence and risk factors.
-
Actuarial Science: Actuaries assess and manage financial risks, often using probability and proportions to predict future events and price insurance policies.
-
Market Research: Market researchers use sample data to understand consumer preferences and trends, making inferences about a larger population.
-
Quality Control: In manufacturing, quality control engineers use statistical techniques to monitor production processes and identify potential defects.
Dealing with Uncertainty: Confidence Intervals and Margin of Error
It's crucial to acknowledge the uncertainty inherent in working with samples. The proportion 25 out of 80,000 is derived from a sample, and it's only an estimate of the true proportion in the population. To account for this uncertainty, we use confidence intervals. A 95% confidence interval, for instance, provides a range within which we are 95% confident the true population proportion lies. The margin of error, usually expressed as a percentage, quantifies the uncertainty associated with the sample estimate.
Further Considerations and Advanced Techniques
More advanced statistical techniques can be applied to analyze data like 25 out of 80,000, depending on the specific research question and data characteristics. These techniques include:
-
Bayesian Statistics: Bayesian methods allow for the incorporation of prior knowledge and beliefs when analyzing data, updating those beliefs as new evidence becomes available.
-
Regression Analysis: Regression models can be used to investigate the relationship between the observed proportion and other relevant variables.
-
Survival Analysis: This type of analysis is often employed when analyzing time-to-event data, such as the time until a product fails or a patient experiences a relapse.
Conclusion: The Power of Context and Critical Analysis
The simple fraction 25 out of 80,000 holds much more significance than its face value suggests. Its interpretation is heavily reliant on context, requiring a thorough understanding of probability, statistics, and the specific field of application. While the raw proportion offers a starting point, the application of statistical techniques and critical analysis is crucial for deriving meaningful insights and making informed decisions. The key takeaway is the imperative to avoid superficial interpretations and instead focus on the underlying principles and the nuances that influence the interpretation of such data. Always consider the context, the limitations of the data, and the potential implications before drawing conclusions. The numbers themselves tell only part of the story; the context provides the narrative.
Latest Posts
Latest Posts
-
15 Of 450
Sep 21, 2025
-
169 In Feet
Sep 21, 2025
-
135 In Kilos
Sep 21, 2025
-
168lb In Kg
Sep 21, 2025
-
53 6kg In Stone
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 80000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.