15 Of 450
interactiveleap
Sep 21, 2025 · 5 min read
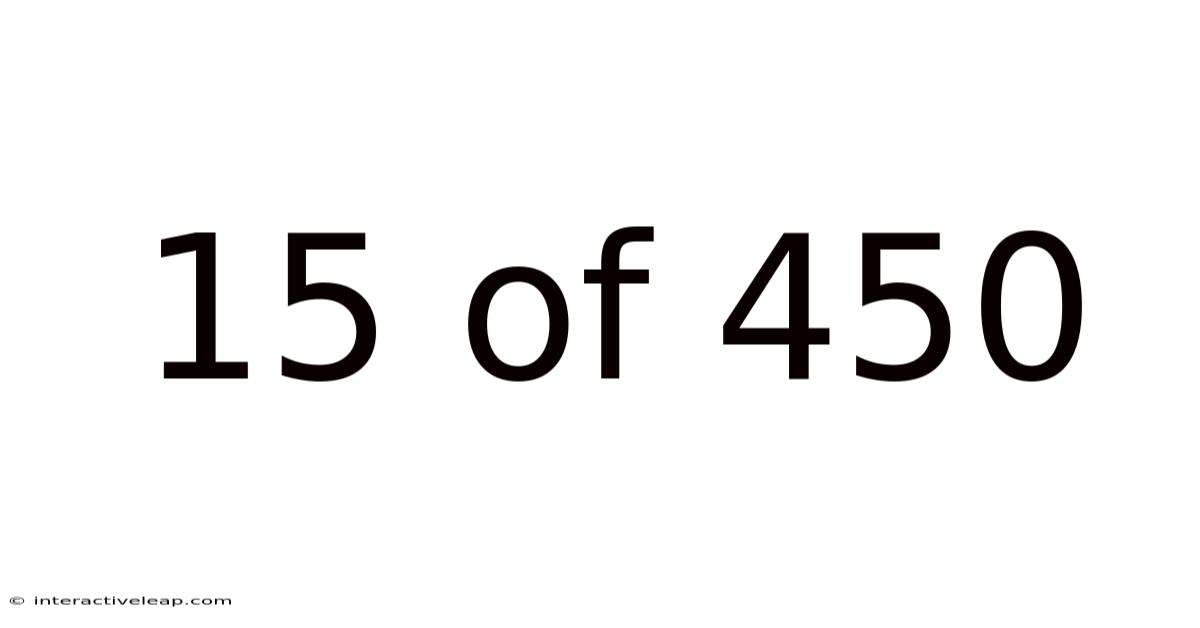
Table of Contents
Decoding the Fraction: Understanding 15 out of 450
The seemingly simple fraction 15/450 represents more than just a mathematical expression; it's a concept that underpins many aspects of our daily lives, from calculating percentages in sales to understanding statistical probabilities. This article will delve into a comprehensive exploration of this fraction, examining its simplification, its percentage equivalent, real-world applications, and related mathematical concepts. We'll unravel its meaning and demonstrate how to confidently handle similar fractional representations.
Simplifying the Fraction: Finding the Lowest Terms
The first step in understanding 15/450 is to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of both the numerator (15) and the denominator (450) and dividing both by that number.
Let's find the GCD of 15 and 450. One method is to list the factors of each number:
- Factors of 15: 1, 3, 5, 15
- Factors of 450: 1, 2, 3, 5, 6, 9, 10, 15, 18, 25, 30, 45, 50, 75, 90, 150, 225, 450
The greatest common factor is 15.
Now, we divide both the numerator and the denominator by 15:
15 ÷ 15 = 1 450 ÷ 15 = 30
Therefore, the simplified fraction is 1/30. This simplified form is much easier to work with and understand.
Converting to Percentage: Expressing the Fraction as a Proportion
Converting a fraction to a percentage provides a readily understandable representation of the fraction's proportion. To convert 1/30 to a percentage, we perform the following calculation:
(1/30) * 100% = 3.333...%
This means that 15 out of 450 represents approximately 3.33%. The recurring decimal indicates that the percentage is a non-terminating decimal, meaning it continues infinitely. For practical purposes, rounding to two decimal places (3.33%) is usually sufficient.
Real-World Applications: Seeing the Fraction in Action
The fraction 15/450, or its simplified form 1/30, appears in numerous real-world scenarios. Let's explore a few examples:
- Test Scores: Imagine a student scoring 15 out of 450 points on a major exam. Their score translates to a 3.33% pass rate, highlighting the need for significant improvement.
- Surveys and Polls: If 15 out of 450 respondents answered "yes" to a particular question in a survey, the result indicates a 3.33% positive response rate.
- Manufacturing Defects: In a production run of 450 items, if 15 are found to be defective, the defect rate is 3.33%. This information is crucial for quality control and process improvement.
- Financial Investments: Consider a portfolio with 15 shares of a particular stock out of a total of 450 shares. The stock represents 3.33% of the entire portfolio's composition.
Understanding Proportions and Ratios: The Bigger Picture
The fraction 15/450 is fundamentally a ratio expressing the relationship between two quantities. It shows the proportion of 15 compared to 450. Understanding ratios is key to solving many problems involving proportions, percentages, and rates.
Let's look at some related concepts:
- Direct Proportion: If two quantities are directly proportional, an increase in one quantity leads to a proportional increase in the other. For example, if you increase the number of hours you work, your earnings will increase proportionally (assuming a constant hourly rate).
- Inverse Proportion: If two quantities are inversely proportional, an increase in one quantity leads to a proportional decrease in the other. For example, the time it takes to complete a journey is inversely proportional to the speed of travel.
- Rates: Rates express the relationship between two quantities with different units. Speed (kilometers per hour), price per unit, and fuel efficiency (kilometers per liter) are examples of rates. The fraction 15/450 could represent a rate if the units are defined (e.g., 15 defective items per 450 items produced).
Solving Problems with Fractions: Practical Examples
Let's consider some problems involving similar fractions to further solidify our understanding:
Problem 1: A farmer harvests 25 apples from a tree that produces 750 apples in total. What percentage of the total apple yield did the farmer harvest?
This problem is analogous to 15/450. We can express the harvested apples as a fraction: 25/750. Simplifying this fraction, we get 1/30, which is equivalent to approximately 3.33%.
Problem 2: In a class of 300 students, 10 students failed a particular subject. What percentage of students failed the subject?
The fraction representing failing students is 10/300. This simplifies to 1/30, equivalent to approximately 3.33%.
These examples demonstrate how the concept of 15/450 and its simplified form, 1/30, can be applied to various real-world situations involving proportions and percentages.
Further Exploration: Expanding Mathematical Knowledge
Understanding 15/450 opens the door to exploring more advanced mathematical concepts:
- Probability: Fractions are fundamental to probability calculations. The fraction represents the likelihood of a specific event occurring. For example, if you randomly select one item from a batch of 450 items, the probability of selecting a defective item (assuming 15 are defective) is 15/450, or 1/30.
- Statistics: Fractions and percentages are essential tools in statistical analysis. Data is often presented as fractions or percentages to convey trends and relationships within datasets.
- Algebra: Fractions are used extensively in algebraic equations and expressions. Understanding how to manipulate fractions is crucial for solving algebraic problems.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 15/450?
A1: The simplest form of 15/450 is 1/30.
Q2: How do I convert 15/450 to a percentage?
A2: Divide the numerator (15) by the denominator (450) and multiply by 100%. This gives approximately 3.33%.
Q3: Can this fraction be expressed as a decimal?
A3: Yes, 1/30 is equivalent to 0.0333... (a recurring decimal).
Q4: What are some real-world applications of this type of fraction?
A4: Real-world applications include calculating percentages in test scores, surveys, manufacturing defect rates, and financial investments, among others.
Conclusion: Mastering the Fundamentals
Understanding the fraction 15/450, its simplification to 1/30, and its percentage equivalent of approximately 3.33% is not just about mastering a specific mathematical calculation. It's about grasping the fundamental concepts of fractions, ratios, proportions, and percentages – tools that are invaluable in numerous aspects of life, from everyday calculations to complex scientific analyses. By mastering these fundamental concepts, you build a strong foundation for more advanced mathematical learning and problem-solving abilities. The seemingly simple fraction 15/450, therefore, represents a gateway to a broader understanding of the mathematical world around us.
Latest Posts
Latest Posts
-
2 000 Ft
Sep 21, 2025
-
64 Divided 2
Sep 21, 2025
-
3000 Times 12
Sep 21, 2025
-
29cm In Inches
Sep 21, 2025
-
Ml To Mm3
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 450 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.