35 Of 350
interactiveleap
Sep 22, 2025 · 5 min read
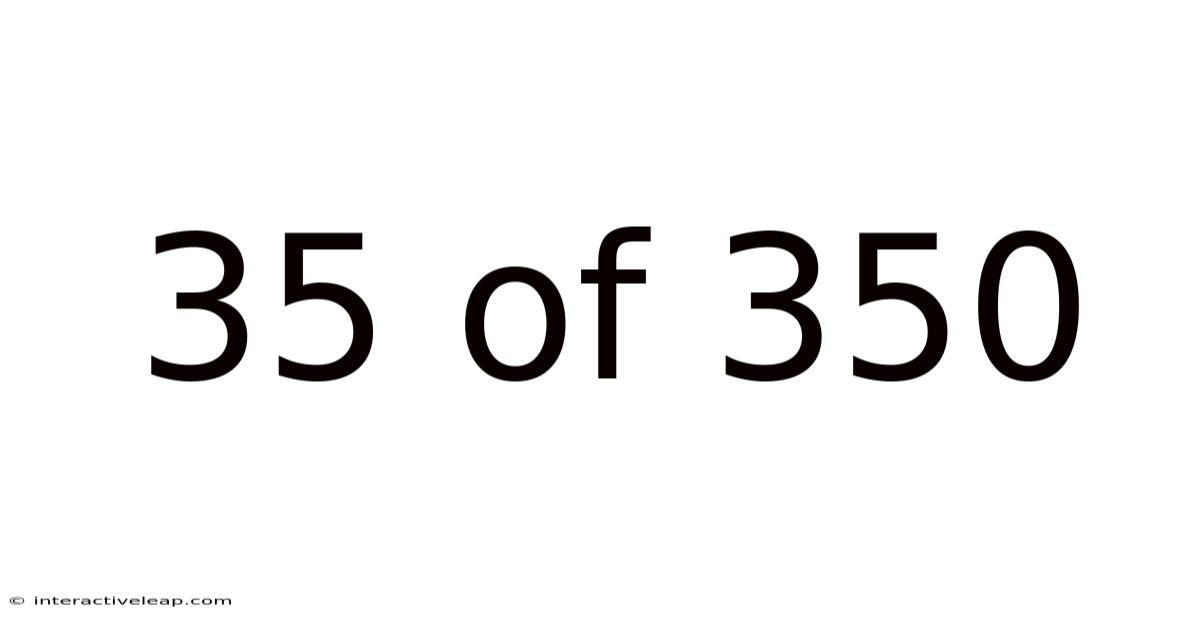
Table of Contents
Decoding the Fraction: Understanding 35/350 and its Implications
The seemingly simple fraction 35/350 might appear straightforward at first glance. However, understanding this fraction goes beyond simply recognizing its numerical value. It opens doors to exploring concepts like simplification, ratios, percentages, and their practical applications in various fields. This article will delve into a comprehensive analysis of 35/350, exploring its mathematical properties and real-world interpretations. We'll cover simplification, equivalent fractions, decimal conversion, percentage representation, and discuss its relevance in different contexts, providing a thorough understanding suitable for students and anyone curious about the power of fractions.
Simplifying the Fraction: Finding the Lowest Terms
The foundation of understanding any fraction lies in its simplified form. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator (top number) and the denominator (bottom number) by their greatest common divisor (GCD). Let's find the GCD of 35 and 350.
Both 35 and 350 are divisible by 5, and 7. To find the GCD, let's perform prime factorization:
- 35 = 5 x 7
- 350 = 2 x 5 x 5 x 7 = 2 x 5² x 7
The common factors are 5 and 7. Therefore, the GCD of 35 and 350 is 5 x 7 = 35.
Now, we can simplify the fraction:
35/350 = (35 ÷ 35) / (350 ÷ 35) = 1/10
Therefore, the simplified form of 35/350 is 1/10. This simplified form makes calculations and comparisons much easier.
Equivalent Fractions: Exploring Different Representations
While 1/10 is the simplest form, there are infinitely many equivalent fractions representing the same value. Any fraction obtained by multiplying both the numerator and the denominator of 1/10 by the same non-zero number will be equivalent. For example:
- 2/20 (multiplying by 2)
- 3/30 (multiplying by 3)
- 4/40 (multiplying by 4)
- 5/50 (multiplying by 5)
- ...and so on.
These fractions, though different in appearance, all represent the same proportion or part of a whole as 1/10 and 35/350. Understanding equivalent fractions is crucial for solving problems involving proportions and ratios.
Converting to Decimal: Expressing the Fraction Numerically
Converting a fraction to a decimal involves dividing the numerator by the denominator. In the case of 1/10:
1 ÷ 10 = 0.1
Therefore, the decimal representation of 35/350 (and its simplified form 1/10) is 0.1. This decimal form is useful in various applications, particularly when dealing with calculations involving other decimal numbers.
Representing as a Percentage: Understanding Proportions
Percentages are a way of expressing fractions as parts of 100. To convert a fraction to a percentage, we multiply the decimal representation by 100:
0.1 x 100 = 10%
Therefore, 35/350 represents 10%. This percentage representation provides a readily understandable way to communicate proportions, making it particularly useful in contexts like statistics, finance, and everyday life. For instance, if 35 out of 350 students passed an exam, we can say that 10% of the students passed.
Real-World Applications: Exploring Practical Scenarios
The fraction 35/350, and its equivalent forms, appear in numerous real-world situations. Here are a few examples:
- Test Scores: If a student answers 35 out of 350 questions correctly on a test, their score is 10%.
- Sales and Discounts: A 10% discount on a product priced at $350 would amount to a reduction of $35.
- Surveys and Statistics: If 35 out of 350 people surveyed prefer a particular brand, the brand enjoys a 10% market share.
- Recipe Scaling: If a recipe calls for 35 grams of sugar in a 350-gram cake, the sugar constitutes 10% of the cake's weight.
- Financial Investments: A 10% return on a $350 investment would yield a profit of $35.
These examples highlight the versatility of the fraction 35/350 and its simplified equivalent, 1/10, in practical applications across diverse fields.
Further Exploration: Expanding Mathematical Understanding
Beyond the basic concepts, exploring 35/350 opens avenues to delve deeper into mathematical ideas:
- Ratios: The fraction represents a ratio of 1:10, signifying a comparison between two quantities.
- Proportions: The fraction can be used to solve problems involving proportional relationships.
- Probability: In certain contexts, the fraction might represent the probability of an event occurring.
- Algebra: Fractions are fundamental elements in algebraic equations and manipulations.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 35/350?
A1: The simplest form of 35/350 is 1/10.
Q2: How do I convert 35/350 to a decimal?
A2: Divide the numerator (35) by the denominator (350). The result is 0.1.
Q3: What is the percentage equivalent of 35/350?
A3: The percentage equivalent is 10%.
Q4: Are there other fractions equivalent to 35/350?
A4: Yes, infinitely many. Any fraction obtained by multiplying both the numerator and denominator of 1/10 by the same non-zero number will be equivalent.
Q5: What are some real-world applications of this fraction?
A5: This fraction can represent proportions in various scenarios, such as test scores, sales discounts, surveys, and recipes.
Conclusion: The Significance of Understanding Fractions
Understanding fractions like 35/350 is not just about performing calculations; it’s about grasping the fundamental concepts of proportions, ratios, and their applications in various aspects of life. By simplifying the fraction to its lowest terms, converting it to a decimal and a percentage, and exploring its real-world applications, we gain a deeper appreciation for the power and versatility of fractions. This knowledge forms a crucial base for further mathematical exploration and problem-solving in numerous fields. The seemingly simple fraction 35/350 serves as a gateway to a wider understanding of mathematical concepts and their practical implications.
Latest Posts
Latest Posts
-
80 Of 64
Sep 22, 2025
-
Butterflies And Symmetry
Sep 22, 2025
-
82kilos In Stone
Sep 22, 2025
-
65 In Binary
Sep 22, 2025
-
98kg In Stones
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 35 Of 350 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.