65 In Binary
interactiveleap
Sep 22, 2025 · 6 min read
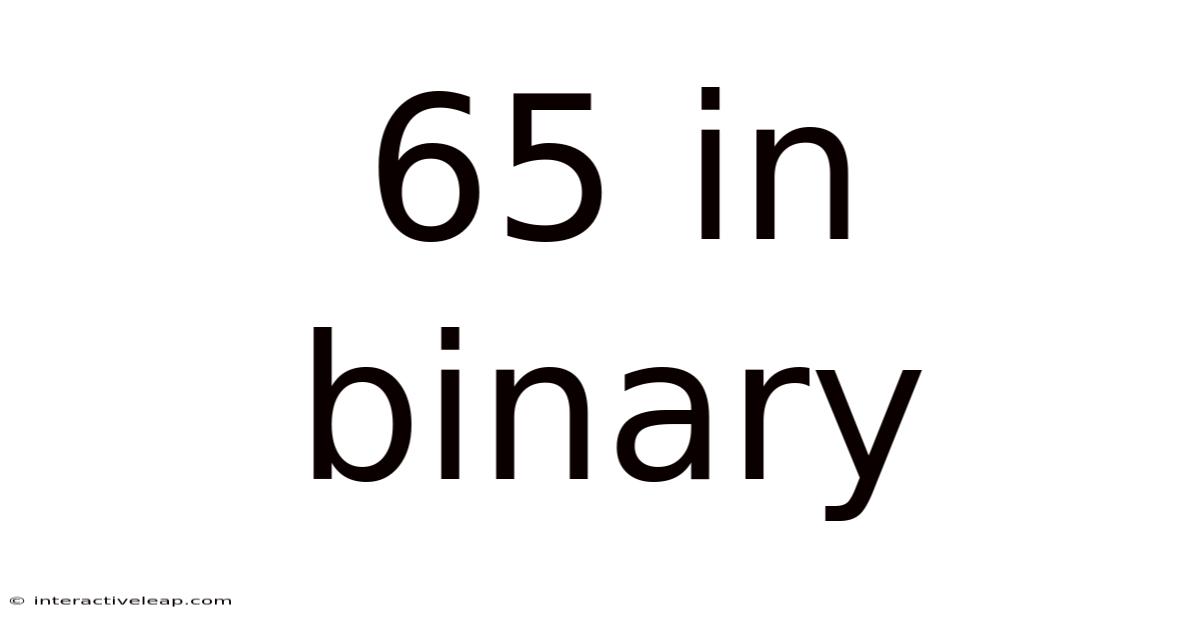
Table of Contents
Decoding 65 in Binary: A Deep Dive into Number Systems
The seemingly simple number 65 holds a fascinating complexity when we explore its representation in different number systems. This article will serve as a comprehensive guide to understanding how 65 is represented in binary, the foundation of all digital computation, and delve into the broader context of number systems and their applications. We'll explore the conversion process, the underlying principles, and some practical applications of binary representation. By the end, you'll not only know that 65 in binary is 1000001, but you'll also grasp the fundamental concepts that make this conversion possible and relevant.
Introduction: Understanding Number Systems
Before diving into the specifics of converting 65 to binary, let's establish a foundational understanding of number systems. We are most familiar with the decimal (base-10) system, where we use ten digits (0-9) to represent numbers. Each place value represents a power of 10. For example, the number 65 in decimal is:
(6 * 10¹) + (5 * 10⁰) = 60 + 5 = 65
Binary (base-2), on the other hand, uses only two digits: 0 and 1. Each place value represents a power of 2. This seemingly limited system is the cornerstone of digital electronics because it's easy to represent physically using electronic switches (on = 1, off = 0).
Other number systems exist, such as octal (base-8) and hexadecimal (base-16), but binary is the most fundamental for computers.
Converting Decimal to Binary: Methods and Explanation
There are several ways to convert a decimal number like 65 to its binary equivalent. We'll explore two common methods:
Method 1: Repeated Division by 2
This is a straightforward and widely used method. We repeatedly divide the decimal number by 2 and record the remainders. The binary representation is formed by reading the remainders from bottom to top.
Let's convert 65 to binary using this method:
| Division | Quotient | Remainder |
|---|---|---|
| 65 / 2 | 32 | 1 |
| 32 / 2 | 16 | 0 |
| 16 / 2 | 8 | 0 |
| 8 / 2 | 4 | 0 |
| 4 / 2 | 2 | 0 |
| 2 / 2 | 1 | 0 |
| 1 / 2 | 0 | 1 |
Reading the remainders from bottom to top, we get 1000001. Therefore, 65 in decimal is 1000001 in binary.
Method 2: Place Value Method
This method involves finding the largest power of 2 that is less than or equal to the decimal number and then subtracting it. We repeat this process until we reach 0.
Let's convert 65 using this method:
- The largest power of 2 less than or equal to 65 is 2⁶ (64). 65 - 64 = 1.
- We have a remainder of 1. The next power of 2 is 2⁰ (1). 1 - 1 = 0.
- Since all remainders have been accounted for, we've exhausted our number.
The powers of 2 used are 2⁶ and 2⁰, represented as 1 and 0 respectively in binary form. Putting them together, we have 1000001 (2⁶ + 2⁰ = 65). Notice that any power of 2 that was not used results in a 0 in the respective binary position.
Understanding the Binary Representation of 65
The binary number 1000001 directly translates to:
(1 * 2⁶) + (0 * 2⁵) + (0 * 2⁴) + (0 * 2³) + (0 * 2²) + (0 * 2¹) + (1 * 2⁰) = 64 + 1 = 65
Each digit (bit) in a binary number represents a power of 2. The rightmost bit is the least significant bit (LSB), representing 2⁰, while the leftmost bit is the most significant bit (MSB), representing the highest power of 2.
Binary in Computer Science and Beyond
The binary number system is fundamental to computer science and digital electronics. Computers operate using binary because it's easy to represent and manipulate electronically using transistors.
- Data Storage: All data, including text, images, audio, and video, is ultimately stored in computers as sequences of binary digits (bits). Each bit represents a 0 or 1 state.
- Computer Instructions: The instructions that a computer executes are also represented in binary code. This code is known as machine code.
- Digital Logic: Binary logic forms the basis of digital circuits and gates (AND, OR, NOT gates), which are the building blocks of all digital electronic devices.
- Network Communication: Data transmitted across networks (like the internet) is also encoded in binary format.
Practical Applications and Examples
Let's explore some practical examples to solidify our understanding:
- ASCII Code: The American Standard Code for Information Interchange (ASCII) uses 7-bit binary numbers to represent characters. For example, the uppercase letter 'A' is represented as 1000001 in binary (which is 65 in decimal). This highlights the direct link between decimal and binary representations within the context of character encoding.
- Image Representation: Images are represented as a grid of pixels, with each pixel's color encoded in binary. The more bits used per pixel, the more colors and detail the image can display.
- Audio Representation: Sound waves are sampled and converted into digital data, represented in binary format. The sampling rate and bit depth determine the quality of the audio.
Frequently Asked Questions (FAQ)
-
Q: Why is binary so important in computing? A: Binary's simplicity (only two states, 0 and 1) makes it easily implemented using electronic switches (transistors), which are the fundamental building blocks of computer hardware.
-
Q: Can I convert any decimal number to binary? A: Yes, any positive integer can be converted to its binary equivalent using the methods described above.
-
Q: What about negative numbers and floating-point numbers? A: Representing negative numbers and floating-point numbers requires more sophisticated techniques, such as two's complement and IEEE 754 standard, respectively. These are more advanced topics but build upon the fundamental concept of binary representation.
-
Q: Is there a limit to the size of a binary number? A: Theoretically, no. The size of a binary number is only limited by the available memory or storage capacity.
Conclusion: Mastering Binary Representation
Understanding the binary representation of numbers, such as 65 (1000001), is crucial for anyone wanting to delve deeper into computer science, digital electronics, or any field involving digital systems. While the concept may seem initially daunting, the repeated division method and the place value method provide clear and accessible pathways to mastering this fundamental skill. Remember, the simplicity of binary – its reliance on only two digits – belies its immense power and fundamental role in shaping our modern digital world. By grasping the underlying principles, you've unlocked a key to comprehending the language of computers. This understanding will empower you to explore more advanced topics in computer science and related fields with a solid foundational knowledge of binary representation.
Latest Posts
Related Post
Thank you for visiting our website which covers about 65 In Binary . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.