34 Of 120
interactiveleap
Sep 20, 2025 · 6 min read
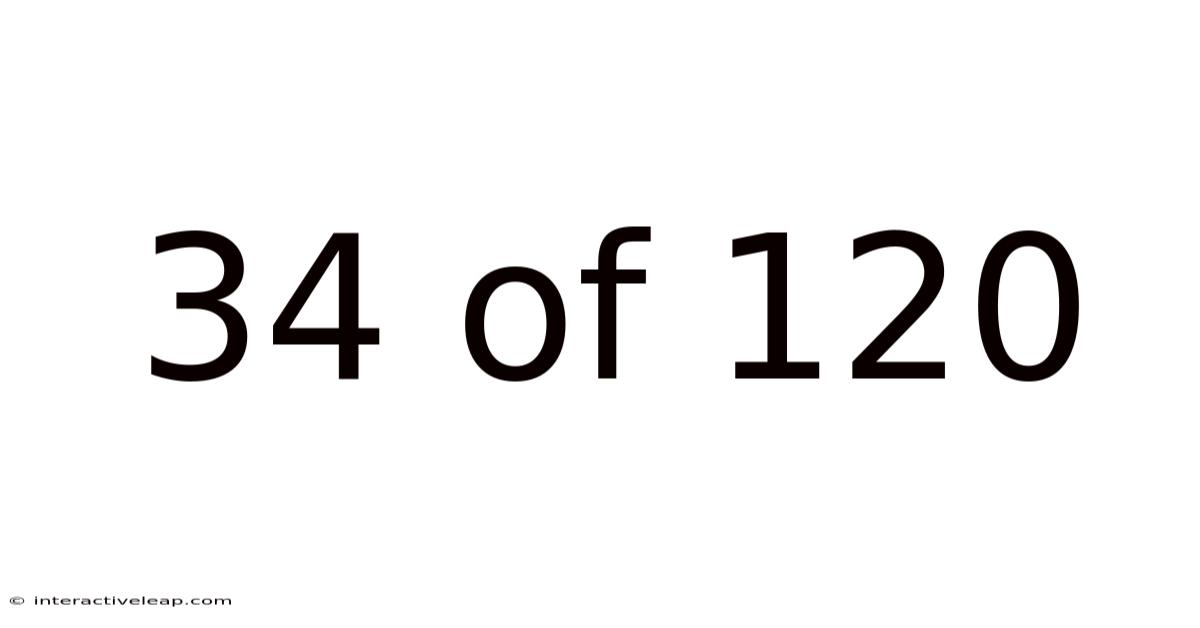
Table of Contents
Decoding 34 of 120: Understanding Fractions, Percentages, and Ratios
The seemingly simple phrase "34 of 120" can represent a variety of mathematical concepts, depending on the context. This article will delve into the meaning and interpretation of this phrase, exploring its representation as a fraction, a percentage, and a ratio, and expanding on the broader mathematical principles involved. Understanding these concepts is crucial for various applications, from everyday calculations to advanced scientific analysis. We'll also address common misconceptions and provide practical examples to solidify your understanding.
Understanding the Core Concepts
Before diving into the specific calculations, let's review the fundamental concepts of fractions, percentages, and ratios:
-
Fractions: A fraction represents a part of a whole. It's expressed as a/b, where 'a' is the numerator (the part) and 'b' is the denominator (the whole). For instance, 1/2 represents one half of a whole.
-
Percentages: A percentage is a fraction expressed as a number out of 100. It signifies a proportion or rate per hundred. The symbol "%" is used to represent percentage. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
-
Ratios: A ratio compares two or more quantities. It can be expressed in different forms, such as a:b or a/b, where 'a' and 'b' represent the quantities being compared. For example, a ratio of 2:3 indicates that for every 2 units of one quantity, there are 3 units of another.
34 of 120 as a Fraction
The simplest interpretation of "34 of 120" is as a fraction. This means 34 represents the part and 120 represents the whole. Therefore, the fraction is written as:
34/120
This fraction can be simplified by finding the greatest common divisor (GCD) of 34 and 120. The GCD of 34 and 120 is 2. Dividing both the numerator and the denominator by 2, we get the simplified fraction:
17/60
This simplified fraction, 17/60, represents the most concise and accurate fractional representation of "34 of 120". It means that 17 out of every 60 parts constitute the original 34 out of 120.
34 of 120 as a Percentage
To express "34 of 120" as a percentage, we need to convert the fraction 34/120 into a percentage. We can do this by dividing the numerator by the denominator and then multiplying by 100:
(34/120) * 100 = 0.28333... * 100 ≈ 28.33%
Therefore, 34 out of 120 is approximately 28.33%. The three recurring decimal places indicate that this is an approximation, and the precise percentage is a non-terminating decimal. For practical purposes, rounding to two decimal places (28.33%) is generally sufficient.
34 of 120 as a Ratio
"34 of 120" can also be represented as a ratio. A ratio compares the part (34) to the whole (120). This ratio can be expressed as:
34:120
Similar to the fraction, this ratio can be simplified by dividing both numbers by their GCD (2):
17:60
This simplified ratio, 17:60, means that for every 17 parts of one quantity, there are 60 parts of the whole quantity. This ratio is equivalent to the simplified fraction 17/60.
Real-World Applications and Examples
The concept of expressing a part of a whole as a fraction, percentage, or ratio is ubiquitous in daily life and various fields:
-
Sales and Marketing: If a company sells 34 units out of a total production of 120 units, they can represent their sales as 28.33% of their production. This helps in analyzing sales performance and making informed business decisions.
-
Statistics and Data Analysis: In surveys or experiments, the results are often represented as fractions, percentages, or ratios to understand the distribution and proportion of different outcomes. For example, if 34 out of 120 respondents answered "yes" to a survey question, this can be expressed as 17/60 or approximately 28.33%.
-
Finance and Investment: When calculating returns on investment (ROI), we use percentages to express the gains or losses relative to the initial investment.
-
Scientific Research: Ratios and percentages are frequently used in scientific studies to compare different groups or variables.
-
Cooking and Baking: Recipes often express the quantities of ingredients as ratios or fractions. For instance, a recipe might call for a 2:1 ratio of flour to sugar.
Addressing Common Misconceptions
-
Confusion between fractions, percentages, and ratios: While closely related, these concepts have distinct interpretations. Fractions represent parts of a whole, percentages are fractions expressed relative to 100, and ratios compare two or more quantities.
-
Difficulty in simplifying fractions and ratios: Finding the GCD is crucial for simplifying fractions and ratios. Practicing with different numbers helps improve proficiency in this area.
-
Incorrect conversion between fractions and percentages: Remember to divide the numerator by the denominator and multiply by 100 to convert a fraction into a percentage.
Expanding Your Knowledge
To further enhance your understanding, you can explore more advanced topics such as:
-
Proportions: Proportions involve comparing two ratios. Understanding proportions is fundamental for solving various problems involving scaling and similar figures.
-
Decimals: Decimals provide another way to represent fractions and percentages, offering a different perspective on representing parts of a whole.
-
Algebraic expressions: Algebra can be used to represent and solve problems involving fractions, percentages, and ratios in a more generalized way.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of the fraction 34/120?
A1: The simplest form is 17/60.
Q2: How do I convert a fraction to a percentage?
A2: Divide the numerator by the denominator and multiply the result by 100.
Q3: What is the difference between a ratio and a fraction?
A3: While both compare quantities, a fraction represents a part of a whole, while a ratio compares two or more quantities. They can be mathematically equivalent but represent different conceptual viewpoints.
Q4: Can a percentage be greater than 100%?
A4: Yes. A percentage greater than 100% indicates that the part is larger than the whole. This is often encountered when comparing changes over time or comparing quantities where one is larger than the initial value.
Conclusion
Understanding how to represent "34 of 120" as a fraction, percentage, and ratio is a fundamental skill in mathematics with broad applications across various fields. By grasping the core concepts and practicing conversions, you'll develop a strong foundation for tackling more complex mathematical problems. Remember that mastering these concepts is not just about memorizing formulas; it's about developing an intuitive understanding of how these different representations relate to each other and how they can be used to analyze and interpret data effectively. Continued practice and exploration will solidify your understanding and allow you to confidently apply these principles in various contexts.
Latest Posts
Latest Posts
-
1 4 9
Sep 20, 2025
-
30 Of 57
Sep 20, 2025
-
25 Square Meters
Sep 20, 2025
-
3 0 75
Sep 20, 2025
-
Suzuki Drz 125
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 34 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.