3 X 9
interactiveleap
Sep 14, 2025 · 7 min read
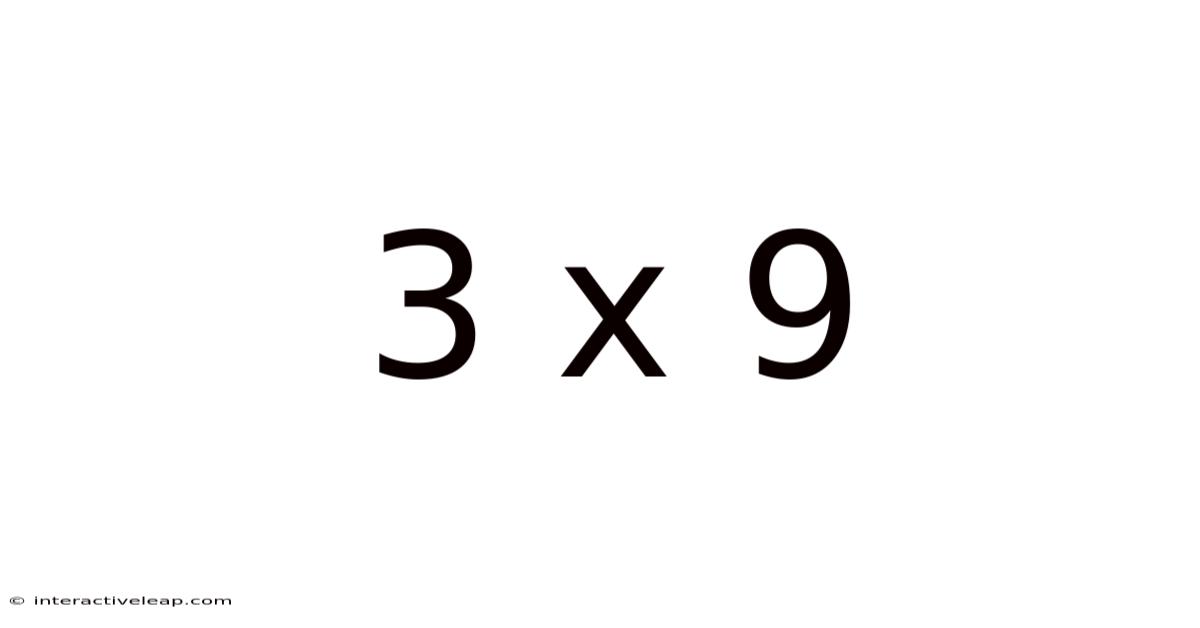
Table of Contents
Exploring the Mathematical Landscape of 3 x 9: From Basic Multiplication to Advanced Applications
The seemingly simple equation, 3 x 9, serves as a gateway to understanding a wide range of mathematical concepts, from fundamental arithmetic to more complex algebraic manipulations and even applications in real-world scenarios. This article delves deep into the multifaceted nature of 3 x 9, exploring its basic calculation, its implications in various mathematical fields, and its practical applications. We'll uncover hidden patterns, explore related concepts, and ultimately demonstrate how a seemingly simple calculation can unlock a wealth of mathematical understanding.
Understanding the Fundamentals: What is 3 x 9?
At its core, 3 x 9 represents the multiplication of the integer 3 by the integer 9. Multiplication, in its simplest form, is repeated addition. Therefore, 3 x 9 can be interpreted as adding the number 3 nine times: 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 27. The answer, 27, is the product of this multiplication. This foundational understanding is crucial for grasping more advanced concepts built upon this simple operation.
Beyond the Basics: Exploring Related Concepts
While the calculation itself is straightforward, exploring related concepts significantly expands our mathematical understanding. Let's examine some key areas:
1. Multiplication Tables and Number Patterns:
The equation 3 x 9 sits within the broader context of multiplication tables. Understanding multiplication tables helps develop number sense and provides a foundation for more complex calculations. Recognizing that 3 x 9 is part of the 3 times table and the 9 times table reveals inherent patterns and relationships within the number system. For example, observing the products of 3 multiplied by consecutive integers (3 x 1, 3 x 2, 3 x 3, etc.) reveals an arithmetic sequence where the difference between consecutive terms is consistently 3. Similarly, the 9 times table displays a fascinating pattern where the sum of the digits in each product always adds up to 9 (or a multiple of 9). For instance, in 9 x 1 = 9, the digit sum is 9; in 9 x 2 = 18, the digit sum is 1 + 8 = 9; and so on. Understanding these patterns significantly enhances mathematical fluency.
2. Factors and Multiples:
The numbers 3 and 9 are both factors of 27. Factors are numbers that divide evenly into a larger number without leaving a remainder. Conversely, 27 is a multiple of both 3 and 9. Multiples are numbers obtained by multiplying a given number by an integer. Understanding factors and multiples is essential for simplifying fractions, solving equations, and working with prime factorization. The prime factorization of 27 is 3 x 3 x 3, or 3³. This reveals the fundamental building blocks of the number 27, highlighting the significance of the number 3 in its composition.
3. Commutative Property of Multiplication:
The commutative property states that the order of the operands in a multiplication operation does not affect the result. In other words, 3 x 9 is equal to 9 x 3. This seemingly simple property has profound implications for mathematical operations, allowing for flexibility and simplification in more complex calculations. Understanding the commutative property lays the foundation for grasping more abstract algebraic concepts.
4. Distributive Property of Multiplication:
The distributive property allows us to break down complex multiplication problems into simpler ones. For instance, if we wanted to calculate 3 x 12, we could use the distributive property to rewrite it as 3 x (9 + 3), which then simplifies to (3 x 9) + (3 x 3) = 27 + 9 = 36. The distributive property is a cornerstone of algebraic manipulation and is crucial for simplifying and solving equations.
3 x 9 in Different Mathematical Contexts
The seemingly simple equation 3 x 9 extends its influence far beyond basic arithmetic. Let's explore its application in different mathematical areas:
1. Algebra:
In algebra, 3 x 9 can be represented using variables. For example, if we let x = 3 and y = 9, then the equation becomes xy = 27. This simple substitution opens the door to solving more complex algebraic equations. Furthermore, the concept of 3 x 9 can be incorporated into equations involving polynomials, linear equations, and more.
2. Geometry:
Imagine a rectangle with a length of 9 units and a width of 3 units. The area of this rectangle is calculated by multiplying its length and width: 9 x 3 = 27 square units. This demonstrates the direct application of 3 x 9 in geometric calculations of area. This principle extends to more complex geometric shapes and calculations.
3. Number Theory:
Number theory investigates the properties of numbers. The number 27, the product of 3 x 9, possesses various interesting properties. It is a perfect cube (3³), a multiple of 3 and 9, and its divisors include 1, 3, 9, and 27. These properties are explored within the broader context of number theory, uncovering deeper insights into the relationships and patterns within the number system.
4. Calculus:
While not directly used in basic calculus operations, the principles underlying multiplication—repeated addition—are fundamental to understanding concepts like integration and summation. The idea of summing up infinitely small quantities builds upon the basic understanding of repeated addition inherent in 3 x 9.
Real-World Applications of 3 x 9
The practical applications of 3 x 9 extend beyond theoretical mathematics. Here are a few examples:
- Shopping: Imagine buying 3 items that cost $9 each. The total cost is calculated as 3 x $9 = $27.
- Measurement: If you have 3 pieces of wood, each measuring 9 feet long, the total length of wood is 27 feet.
- Baking: A recipe calls for 9 tablespoons of flour per batch, and you want to make 3 batches. You need 3 x 9 = 27 tablespoons of flour.
- Construction: Calculating the number of bricks needed for a wall, or the amount of materials for a project frequently involves multiplication. For example, needing 9 bricks per row and having 3 rows translates into 27 bricks needed.
Frequently Asked Questions (FAQ)
Q: What are some different ways to calculate 3 x 9?
A: Besides direct multiplication, you can use repeated addition (3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3), use a multiplication table, or break down the problem using the distributive property (e.g., 3 x (10 -1) = 30 - 3 = 27).
Q: Is there a quick mental math trick to calculate 3 x 9?
A: While there isn't a single universally quick trick, many people memorize the multiplication tables, making 3 x 9 an immediate recall. Alternatively, you could think of it as 3 x (10 - 1) = 30 - 3 = 27.
Q: What is the significance of the number 27?
A: 27 is a composite number, a perfect cube (3³), and has several interesting mathematical properties within number theory. It is also a multiple of 3 and 9.
Q: How does understanding 3 x 9 help with more advanced mathematics?
A: Understanding the fundamental concepts involved in 3 x 9—such as multiplication, factors, multiples, and the distributive property—forms the bedrock for more advanced mathematical concepts in algebra, geometry, calculus, and number theory.
Conclusion: The Enduring Power of a Simple Equation
The seemingly insignificant equation 3 x 9 unveils a wealth of mathematical knowledge and applications. From basic arithmetic to advanced mathematical concepts and real-world problems, this simple equation serves as a powerful reminder of the interconnectedness of mathematical ideas. By exploring its nuances and related concepts, we not only solidify our understanding of fundamental arithmetic but also build a strong foundation for tackling more complex mathematical challenges. The journey from a basic calculation to a deep understanding highlights the enduring power of simple equations and their significance in shaping our mathematical literacy. The exploration of 3 x 9 is not merely about finding the answer 27; it's about unlocking a broader appreciation for the beauty and power of mathematics itself.
Latest Posts
Latest Posts
-
3000mm To Meters
Sep 14, 2025
-
4 X X2
Sep 14, 2025
-
Information Data Difference
Sep 14, 2025
-
3c To Fahrenheit
Sep 14, 2025
-
Kj In Kw
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3 X 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.