3/7 Of 28
interactiveleap
Sep 22, 2025 · 5 min read
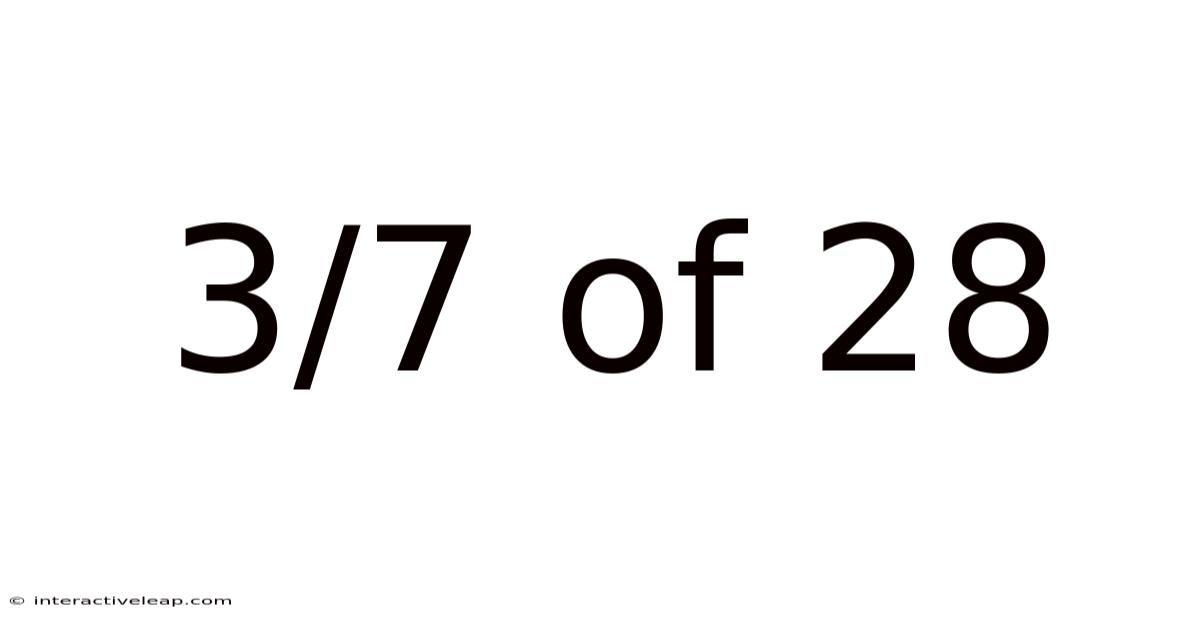
Table of Contents
Unveiling the Mystery: A Deep Dive into 3/7 of 28
Finding 3/7 of 28 might seem like a simple arithmetic problem, suitable only for elementary school. But beneath the surface of this seemingly straightforward calculation lies a wealth of mathematical concepts and practical applications that extend far beyond the basic operation. This article will explore the solution to this problem, delving into the underlying principles of fractions, providing various methods for solving it, and discussing its relevance in real-world scenarios. We will also examine related concepts to enhance your understanding of fractions and their application in mathematics. By the end, you'll not only know the answer to "3/7 of 28" but also possess a deeper understanding of fractional calculations.
Understanding Fractions: The Building Blocks
Before we tackle the problem, let's establish a firm grasp on the fundamental concepts related to fractions. A fraction represents a part of a whole. It consists of two essential components:
- Numerator: The top number in a fraction, indicating the number of parts being considered.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our problem, 3/7, '3' is the numerator and '7' is the denominator. This means we are considering 3 out of 7 equal parts of a whole.
Method 1: Direct Calculation - Multiplication of Fractions
The most straightforward method to find 3/7 of 28 is through direct multiplication. We can express 28 as a fraction with a denominator of 1 (28/1). Then, we multiply the numerators together and the denominators together:
(3/7) * (28/1) = (3 * 28) / (7 * 1) = 84 / 7
Finally, we simplify the resulting fraction by dividing the numerator by the denominator:
84 / 7 = 12
Therefore, 3/7 of 28 is 12.
Method 2: Simplification Before Multiplication
Often, simplifying the fractions before multiplication can make the calculation easier. Notice that 28 is divisible by 7:
28 / 7 = 4
Now, we can rewrite the equation as:
(3/7) * (28/1) = (3/1) * (4/1) = 12
This method highlights the importance of recognizing common factors to streamline the calculation process.
Method 3: Understanding the "Of" Operator
The word "of" in mathematical contexts often signifies multiplication. Therefore, "3/7 of 28" is equivalent to (3/7) * 28. This understanding is crucial in interpreting word problems and translating them into mathematical expressions.
Method 4: Visual Representation
Visualizing the problem can be particularly helpful, especially for those who find abstract mathematical concepts challenging. Imagine a circle divided into 7 equal parts. Each part represents 28/7 = 4. Since we want 3/7 of 28, we simply take 3 of those parts: 3 * 4 = 12. This method provides a concrete, visual understanding of the fractional calculation.
Real-World Applications: Where Fractions Matter
Fractions are not confined to the realm of theoretical mathematics; they permeate various aspects of our daily lives. Here are a few examples:
- Cooking and Baking: Recipes frequently use fractions (e.g., 1/2 cup of sugar, 2/3 cup of flour). Understanding fractions is essential to accurately measure ingredients and ensure successful culinary outcomes.
- Construction and Engineering: Precise measurements and calculations using fractions are critical in construction and engineering projects to ensure structural integrity and functionality.
- Finance and Budgeting: Fractions are indispensable in managing finances, calculating percentages, and understanding interest rates.
- Data Analysis: Many statistical analyses involve the interpretation and manipulation of fractions and percentages. Understanding fractions forms the basis for interpreting data and making informed decisions.
- Time Management: Fractions are frequently used to represent portions of time (e.g., 1/4 of an hour, 2/3 of a day). Effective time management requires an understanding of how to manipulate these fractional representations.
Expanding the Concept: Beyond 3/7 of 28
Let's broaden our perspective beyond this specific problem and explore related concepts:
- Finding a Percentage: Finding a percentage of a number is closely related to finding a fraction of a number. For example, 3/7 is approximately 42.86%. Therefore, finding 3/7 of 28 is equivalent to finding 42.86% of 28.
- Working with Mixed Numbers: A mixed number combines a whole number and a fraction (e.g., 2 1/3). Understanding how to convert mixed numbers to improper fractions (where the numerator is larger than the denominator) is vital for performing calculations involving mixed numbers.
- Adding and Subtracting Fractions: Adding and subtracting fractions require a common denominator. The ability to find the least common multiple (LCM) of two or more numbers is essential for performing these operations efficiently.
- Multiplying and Dividing Fractions: We've already explored multiplying fractions, but dividing fractions also requires understanding the concept of reciprocals (flipping the fraction).
- Fractions and Decimals: Fractions and decimals are interchangeable. Any fraction can be expressed as a decimal, and vice versa. Understanding how to convert between fractions and decimals is crucial for various applications.
Frequently Asked Questions (FAQs)
Q: What is the simplest form of 3/7?
A: 3/7 is already in its simplest form because 3 and 7 have no common factors other than 1.
Q: Can I solve this problem using a calculator?
A: Yes, you can input (3/7) * 28 into a calculator to obtain the answer directly.
Q: What if the numbers were larger or involved decimals?
A: The same principles apply. The direct multiplication method remains effective, though simplification might become more complex. Calculators can be particularly helpful for more intricate calculations.
Q: How do I find a fraction of a decimal number?
A: Convert the decimal to a fraction first, then proceed with the multiplication of fractions.
Q: Are there any online resources that can help me practice?
A: Many educational websites and apps offer practice problems and tutorials on fractions. These can help reinforce your understanding and build your skills.
Conclusion: Mastering Fractions for a Brighter Future
Finding 3/7 of 28, while seemingly trivial at first glance, reveals a rich tapestry of mathematical concepts and practical applications. By understanding the fundamental principles of fractions, mastering different calculation methods, and appreciating their real-world relevance, you equip yourself with a valuable tool applicable across numerous disciplines. The ability to confidently work with fractions opens doors to more advanced mathematical concepts and empowers you to solve complex problems in various contexts. So, the next time you encounter a fraction, remember the power and versatility it holds, extending far beyond simple arithmetic calculations. Mastering fractions is not merely about obtaining the right answer; it's about developing a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
164lbs To Kg
Sep 22, 2025
-
Metallic Hair Dye
Sep 22, 2025
-
Wood Glue Strongest
Sep 22, 2025
-
American Spirit Orange
Sep 22, 2025
-
15 Of 54
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 3/7 Of 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.