15 Of 54
interactiveleap
Sep 22, 2025 · 5 min read
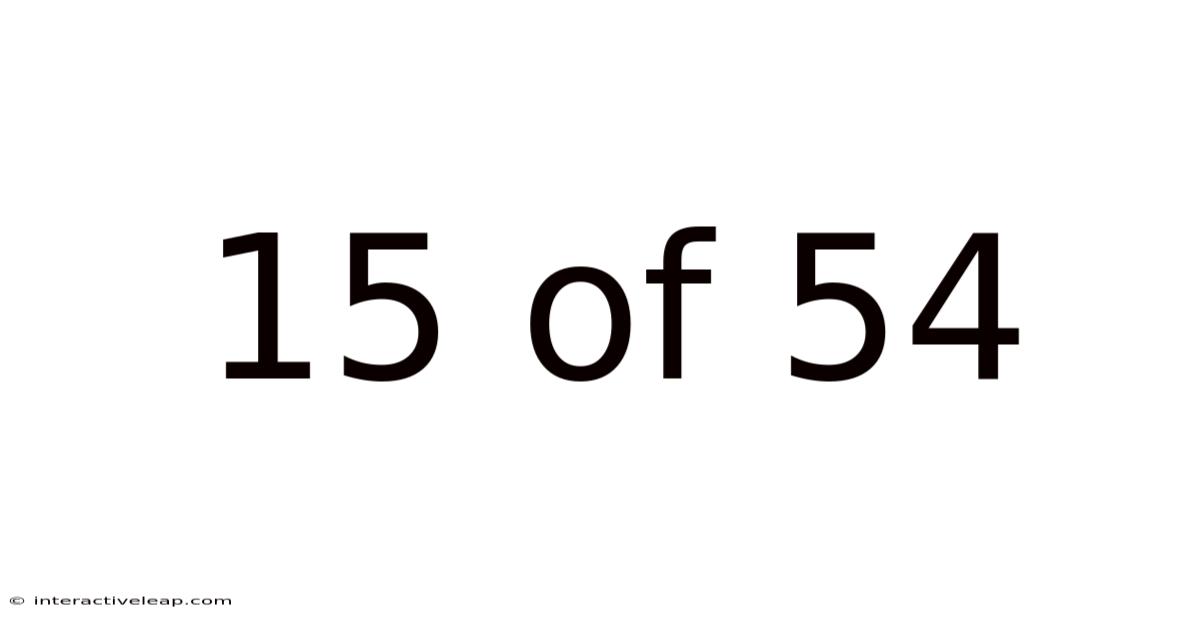
Table of Contents
Decoding the Enigma: Understanding the Fraction 15/54 and its Implications
The seemingly simple fraction 15/54 holds within it a wealth of mathematical concepts and applications. Understanding this fraction goes beyond simple arithmetic; it's a gateway to grasping fundamental principles of fractions, simplification, ratios, and even their visual representations. This article will delve deep into 15/54, exploring its simplification, its decimal equivalent, its applications in real-world scenarios, and addressing common misconceptions surrounding fractions in general.
Introduction: More Than Just Numbers
At first glance, 15/54 appears as a straightforward fraction. However, a deeper understanding reveals its potential for illustrating important mathematical principles. This fraction represents a part-to-whole relationship, where 15 represents a portion of a whole comprised of 54 parts. This article will guide you through the process of simplifying this fraction, converting it to a decimal, and exploring its practical applications. We'll also address common questions and misconceptions about fractions, ensuring you leave with a comprehensive understanding of 15/54 and similar fractional concepts.
Step-by-Step Simplification of 15/54
Simplifying fractions is crucial for making them easier to understand and use. The goal is to reduce the fraction to its simplest form, where the numerator and denominator have no common factors other than 1. This process is also known as finding the greatest common divisor (GCD).
-
Finding the Greatest Common Divisor (GCD): The first step is to find the GCD of 15 and 54. We can do this by listing the factors of each number:
- Factors of 15: 1, 3, 5, 15
- Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
The greatest common factor shared by both 15 and 54 is 3.
-
Dividing the Numerator and Denominator: Now, divide both the numerator (15) and the denominator (54) by the GCD (3):
15 ÷ 3 = 5 54 ÷ 3 = 18
-
Simplified Fraction: This gives us the simplified fraction 5/18. This is the simplest form of 15/54 because 5 and 18 share no common factors other than 1.
Therefore, 15/54 simplifies to 5/18.
Converting 15/54 (or 5/18) to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. For 5/18:
5 ÷ 18 ≈ 0.2777...
The result is a repeating decimal, where the digit 7 repeats infinitely. This is often represented as 0.27̅7̅ or 0.27 recurring.
Visual Representation of 15/54
Imagine a rectangular bar divided into 54 equal parts. Shading 15 of these parts visually represents the fraction 15/54. Similarly, you could visualize 5/18 by dividing a rectangle into 18 equal parts and shading 5 of them. This visual representation helps solidify the understanding of the fraction as a part of a whole.
Real-World Applications of Fractions like 15/54
Fractions are ubiquitous in everyday life. Here are a few examples where a fraction like 15/54 (or its simplified form 5/18) could be applied:
-
Baking: A recipe might call for 15 grams of sugar out of a total of 54 grams of ingredients. This ratio can be simplified to 5/18, meaning sugar constitutes 5/18 of the total ingredients.
-
Probability: If there are 54 marbles in a bag, 15 of which are red, the probability of picking a red marble is 15/54, simplified to 5/18.
-
Measurement: Imagine a project requiring a piece of wood 15 centimeters long from a total length of 54 centimeters. The ratio is 15/54, or 5/18.
-
Geometry: Consider a shape where 15 out of 54 total squares are shaded. The fraction 15/54 (or 5/18) represents the portion of the shape that is shaded.
Understanding the Concept of Ratios
The fraction 15/54 can also be understood as a ratio. Ratios compare two quantities. In this case, the ratio is 15:54, which simplifies to 5:18. This means for every 5 parts of one quantity, there are 18 parts of another. This concept is vital in many fields, including chemistry (mixing solutions), cooking (recipe proportions), and engineering (scaling models).
Addressing Common Misconceptions About Fractions
Many misconceptions surround fractions. Here are some common ones:
-
Fractions are just for kids: Fractions are fundamental mathematical tools used throughout various fields, from engineering and finance to cooking and construction.
-
Simplifying fractions is unnecessary: Simplifying fractions makes calculations easier, and it provides a clearer understanding of the relationship between the numerator and the denominator.
-
Decimal equivalents are always easier: While decimals are sometimes easier to work with, fractions offer a more precise representation, especially for repeating decimals.
-
Adding fractions is simply adding numerators and denominators: Adding fractions requires finding a common denominator before adding the numerators.
Frequently Asked Questions (FAQ)
-
What is the reciprocal of 15/54? The reciprocal is obtained by flipping the fraction: 54/15, which simplifies to 18/5.
-
Can 15/54 be expressed as a mixed number? No, because the numerator (15) is smaller than the denominator (54). A mixed number represents a whole number and a proper fraction.
-
How do I compare 15/54 to other fractions? It's easiest to compare fractions after simplifying them to their lowest terms. Convert them all to decimals if a direct comparison is needed.
-
What are some other fractions that simplify to 5/18? Multiples of the numerator and denominator of 5/18, such as 10/36, 15/54, 20/72 etc., will all simplify to 5/18.
Conclusion: Mastering the Fundamentals
Understanding the fraction 15/54, and its simplified form 5/18, provides a strong foundation in fundamental mathematical concepts. The process of simplification, conversion to decimals, and visualization helps to grasp the essence of fractions. This knowledge extends far beyond basic arithmetic, impacting our understanding of ratios, proportions, probability, and various real-world applications. By addressing common misconceptions and exploring different representations, we can appreciate the multifaceted nature of fractions and their importance in various aspects of life. This deep dive into 15/54 underscores the significance of mastering fundamental mathematical principles, allowing us to navigate complex problems with confidence and clarity. The seemingly simple fraction holds within it a world of mathematical possibilities, and by understanding its nuances, we unlock a broader appreciation for the beauty and utility of mathematics.
Latest Posts
Latest Posts
-
Thousandth To Inches
Sep 22, 2025
-
Lewis Co2 Structure
Sep 22, 2025
-
2x 10 2
Sep 22, 2025
-
Adornos Authoritarian Personality
Sep 22, 2025
-
Caramel Dark Chocolate
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.