2x 10 2
interactiveleap
Sep 22, 2025 · 7 min read
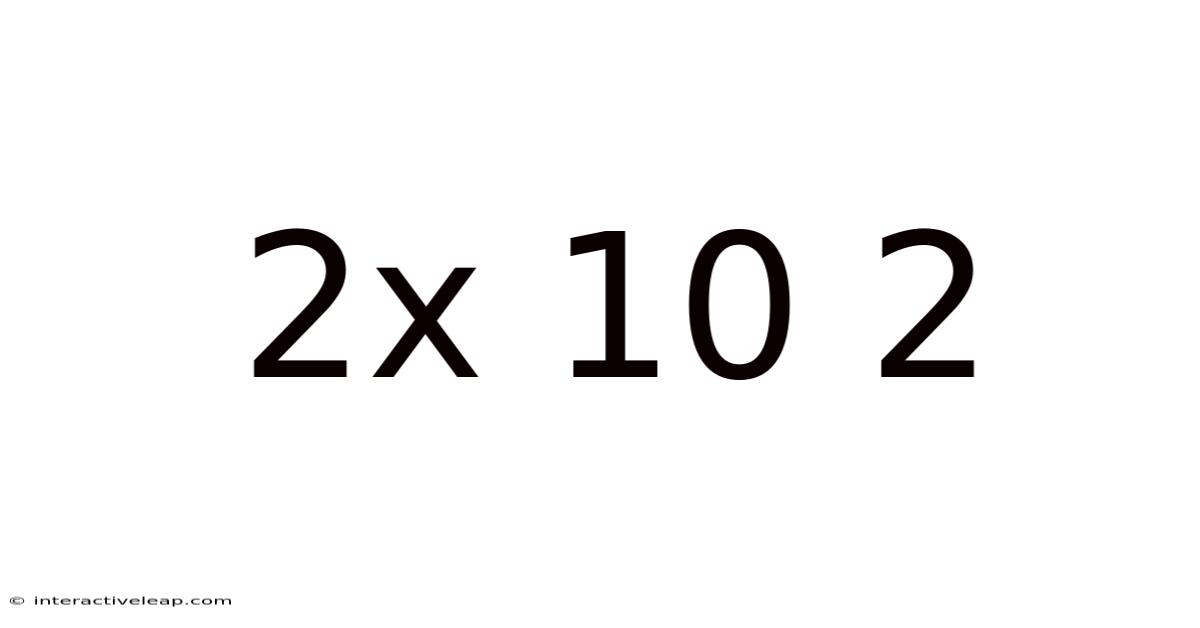
Table of Contents
Decoding 2 x 10<sup>2</sup>: A Deep Dive into Scientific Notation and Exponential Growth
This article explores the seemingly simple mathematical expression "2 x 10<sup>2</sup>," unraveling its significance beyond basic arithmetic. We'll delve into the principles of scientific notation, its applications in various fields, and the broader concept of exponential growth it represents. Understanding this seemingly simple equation opens doors to comprehending complex scientific phenomena and technological advancements.
Introduction: Understanding Scientific Notation
At its core, 2 x 10<sup>2</sup> is an example of scientific notation, a standardized way of writing very large or very small numbers. It's crucial in fields like science, engineering, and computer science where dealing with extremely large or small values is commonplace. Instead of writing out lengthy numbers like 200, scientific notation simplifies the representation.
The general form of scientific notation is: a x 10<sup>b</sup>, where:
- a is a number between 1 and 10 (but not including 10). This is called the coefficient.
- b is an integer (whole number) representing the exponent, indicating the power of 10.
In our example, 2 x 10<sup>2</sup>, a = 2 and b = 2. The exponent, 2, means we multiply 2 by 10 twice (10 x 10 = 100), resulting in 200.
Breaking Down 2 x 10<sup>2</sup>: Step-by-Step
Let's break down the calculation methodically:
-
Identify the coefficient: The coefficient is 2.
-
Identify the exponent: The exponent is 2.
-
Calculate the power of 10: 10<sup>2</sup> means 10 multiplied by itself twice: 10 x 10 = 100.
-
Multiply the coefficient by the power of 10: 2 x 100 = 200.
Therefore, 2 x 10<sup>2</sup> equals 200. This seemingly simple calculation forms the foundation for understanding much more complex scientific concepts.
The Significance of Exponents: Exponential Growth
The exponent in scientific notation isn't just a mathematical operation; it embodies the concept of exponential growth. This is a crucial concept in many areas, including:
-
Population growth: The growth of a population can be modeled using exponential functions. A small initial population can grow dramatically over time if the growth rate remains constant.
-
Compound interest: The interest earned on an investment can compound exponentially, meaning interest is earned not only on the principal but also on the accumulated interest.
-
Viral spread: The spread of a virus or a piece of information can follow an exponential pattern, initially slow but accelerating rapidly as more people become infected or exposed.
-
Technological advancements: Moore's Law, which states that the number of transistors on a microchip doubles approximately every two years, exemplifies exponential growth in the tech industry.
Applications of Scientific Notation Across Disciplines
Scientific notation's value extends far beyond simple arithmetic. Its applications are ubiquitous across numerous fields:
-
Physics: Describing distances in astronomy (e.g., the distance to a star), measuring extremely small particles (e.g., the size of an atom), or dealing with immense energies (e.g., nuclear reactions).
-
Chemistry: Representing the number of atoms or molecules in a substance (Avogadro's number is approximately 6.022 x 10<sup>23</sup>). This is fundamental to stoichiometry and chemical calculations.
-
Biology: Quantifying the number of cells in an organism, measuring concentrations of substances, and describing genetic sequences.
-
Computer Science: Representing large data sets, processing speeds, and memory capacities. The vast amounts of data processed by computers daily often necessitate the use of scientific notation.
-
Engineering: In fields like civil engineering, calculations involving large structures or complex systems frequently utilize scientific notation to manage immense numbers.
Beyond 2 x 10<sup>2</sup>: Expanding the Concept
While 2 x 10<sup>2</sup> provides a straightforward example, scientific notation handles much larger and smaller numbers with equal ease. Consider these examples:
-
6.022 x 10<sup>23</sup> (Avogadro's Number): This number represents the number of atoms or molecules in one mole of a substance. Imagine trying to write this number out without scientific notation – it would be incredibly unwieldy.
-
1.6 x 10<sup>-19</sup> Coulombs (Elementary Charge): This represents the charge of a single electron, an incredibly small quantity. Scientific notation efficiently captures this tiny value.
These examples highlight the power and necessity of scientific notation in representing extreme values concisely and accurately.
Converting to and from Scientific Notation
Converting numbers to and from scientific notation is a valuable skill. Here's a quick guide:
Converting a large number to scientific notation:
- Move the decimal point to the left until you have a number between 1 and 10.
- Count the number of places you moved the decimal point. This is your exponent.
- Write the number in the form a x 10<sup>b</sup>, where a is the number between 1 and 10 and b is the exponent.
Example: Convert 5,200,000 to scientific notation.
- Move the decimal point six places to the left: 5.2
- The exponent is 6.
- The scientific notation is 5.2 x 10<sup>6</sup>.
Converting a small number to scientific notation:
- Move the decimal point to the right until you have a number between 1 and 10.
- Count the number of places you moved the decimal point. This is your negative exponent.
- Write the number in the form a x 10<sup>-b</sup>, where a is the number between 1 and 10 and b is the negative exponent.
Example: Convert 0.0000035 to scientific notation.
- Move the decimal point six places to the right: 3.5
- The exponent is -6.
- The scientific notation is 3.5 x 10<sup>-6</sup>.
Converting from scientific notation to standard notation:
- If the exponent is positive, move the decimal point to the right the number of places indicated by the exponent.
- If the exponent is negative, move the decimal point to the left the number of places indicated by the exponent.
Frequently Asked Questions (FAQ)
Q: Why is scientific notation important?
A: Scientific notation provides a concise and standardized way to represent extremely large or small numbers, simplifying calculations and communication in various scientific and technical fields.
Q: Can I use scientific notation for any number?
A: While you technically can, it's generally most useful for very large or very small numbers. Using it for numbers like 200 is less efficient than simply writing "200."
Q: How do I perform calculations with numbers in scientific notation?
A: When multiplying numbers in scientific notation, multiply the coefficients and add the exponents. When dividing, divide the coefficients and subtract the exponents.
Q: What if the coefficient is not between 1 and 10?
A: If the coefficient is not between 1 and 10, you need to adjust the coefficient and the exponent accordingly to bring it within the standard form of scientific notation.
Q: Are there any limitations to scientific notation?
A: While incredibly useful, scientific notation doesn't directly convey the precision of a measurement. Significant figures are crucial to express accuracy when using scientific notation.
Conclusion: Unlocking the Power of 2 x 10<sup>2</sup> and Beyond
The seemingly simple expression 2 x 10<sup>2</sup> serves as a gateway to understanding the powerful concept of scientific notation and its wide-ranging applications. Mastering this notation is essential for anyone navigating fields that deal with extreme values, from the vastness of space to the intricacies of the atomic world. By grasping the principles of exponential growth inherent in scientific notation, we can better comprehend the dynamic processes shaping our world – from technological advancements to the complexities of natural systems. This understanding not only enhances our mathematical skills but also deepens our understanding of the world around us. The journey from 2 x 10<sup>2</sup> to comprehending Avogadro's number or the elementary charge is a testament to the power and elegance of mathematical representation.
Latest Posts
Latest Posts
-
0 125 To Percentage
Sep 22, 2025
-
25 Of 1300
Sep 22, 2025
-
25 Of 68
Sep 22, 2025
-
2 3 In Percent
Sep 22, 2025
-
147lbs To Kg
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 2x 10 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.