0.125 To Percentage
interactiveleap
Sep 22, 2025 · 5 min read
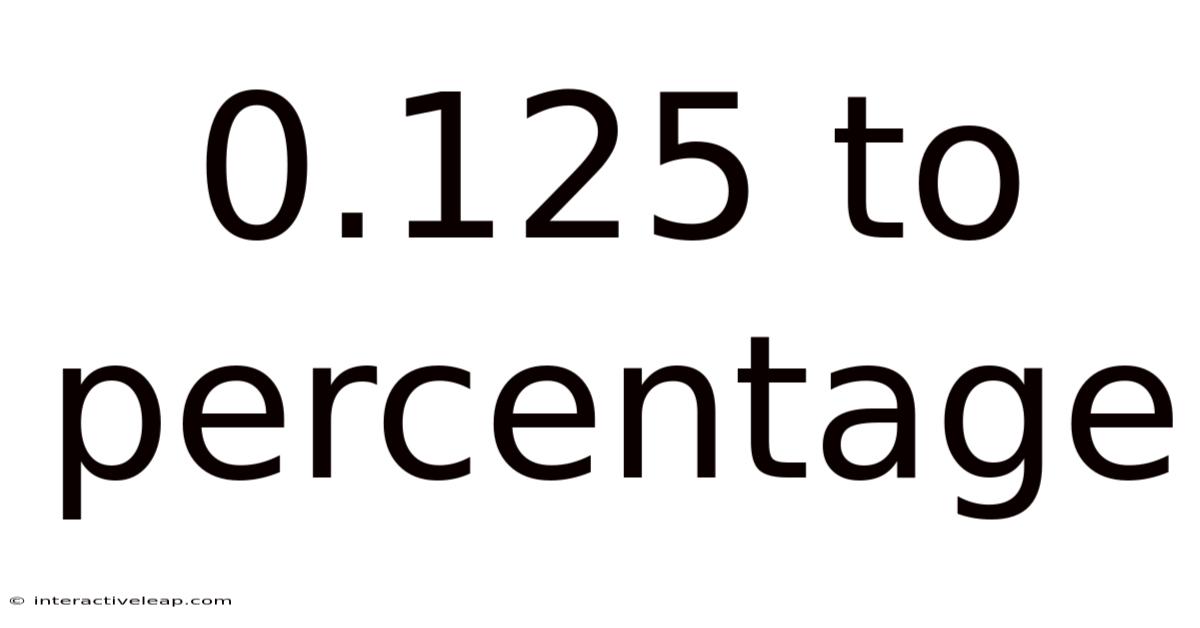
Table of Contents
Converting 0.125 to a Percentage: A Comprehensive Guide
Understanding how to convert decimals to percentages is a fundamental skill in mathematics, crucial for various applications in everyday life, from calculating discounts in shopping to understanding financial reports. This comprehensive guide will walk you through the process of converting the decimal 0.125 to a percentage, explaining the underlying principles and providing you with practical examples. We'll also explore the broader context of decimal-to-percentage conversions and address frequently asked questions. By the end, you'll not only know the answer but also understand the why behind the conversion.
Understanding Decimals and Percentages
Before diving into the conversion, let's clarify the concepts of decimals and percentages. A decimal is a way of representing a number that is not a whole number. It uses a decimal point to separate the whole number part from the fractional part. For instance, 0.125 represents a value less than one.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion relative to a whole. For example, 50% means 50 out of 100, or half. The key to converting between decimals and percentages lies in understanding this relationship to 100.
Converting 0.125 to a Percentage: The Steps
The conversion process is straightforward and involves two simple steps:
Step 1: Multiply by 100
To convert a decimal to a percentage, you multiply the decimal by 100. This is because a percentage is a fraction of 100.
0.125 x 100 = 12.5
Step 2: Add the Percentage Symbol
Once you've multiplied by 100, add the percentage symbol (%) to indicate that the result is a percentage.
Therefore, 0.125 is equivalent to 12.5%.
The Underlying Mathematics: Fractions, Decimals, and Percentages
Let's delve a little deeper into the mathematical principles behind this conversion. The decimal 0.125 can be represented as a fraction:
0.125 = 125/1000
To express this fraction as a percentage, we need to find an equivalent fraction with a denominator of 100. We can simplify the fraction by dividing both the numerator and the denominator by 125:
125/1000 = (125 ÷ 125) / (1000 ÷ 125) = 1/8
Now, to convert the fraction 1/8 to a percentage, we can set up a proportion:
1/8 = x/100
Solving for x:
x = (1/8) * 100 = 12.5
Thus, 1/8 is equivalent to 12.5%, confirming our previous calculation. This demonstrates the interconnectedness of fractions, decimals, and percentages. They are simply different ways of representing the same value.
Practical Applications: Real-World Examples
Understanding decimal-to-percentage conversions is essential in numerous real-world scenarios. Here are a few examples:
-
Discounts: A store offers a 12.5% discount on an item. If the original price is $80, the discount amount would be 12.5% of $80, which is $10 ($80 x 0.125 = $10).
-
Interest Rates: A savings account offers an annual interest rate of 12.5%. This means that for every $100 in the account, you'll earn $12.50 in interest per year.
-
Tax Calculations: Sales tax might be 12.5% in certain regions. To calculate the tax on a purchase, you would multiply the purchase price by 0.125.
-
Data Analysis: In data analysis and statistics, percentages are frequently used to represent proportions and probabilities, often starting from decimal values calculated from data sets.
-
Scientific Measurements: In scientific fields like chemistry or physics, concentrations are often expressed as percentages, derived from decimal representations of ratios.
These are just a few examples illustrating the widespread applicability of understanding decimal-to-percentage conversions. The skill is not limited to mathematical contexts but extends to various real-world situations that demand a grasp of proportions and ratios.
Beyond 0.125: Converting Other Decimals to Percentages
The method described above applies universally to converting any decimal to a percentage. Let's illustrate with a few more examples:
-
0.5: 0.5 x 100 = 50%, representing one-half.
-
0.25: 0.25 x 100 = 25%, representing one-quarter.
-
0.75: 0.75 x 100 = 75%, representing three-quarters.
-
1.5: 1.5 x 100 = 150%, representing one and a half. Note that percentages can exceed 100%.
-
0.05: 0.05 x 100 = 5%, a smaller fraction.
Converting Percentages to Decimals: The Reverse Process
Just as you can convert decimals to percentages, you can also perform the reverse process. To convert a percentage to a decimal, you divide the percentage by 100 and remove the percentage symbol. For example:
-
25% = 25/100 = 0.25
-
150% = 150/100 = 1.5
-
5% = 5/100 = 0.05
Frequently Asked Questions (FAQ)
Q1: What if the decimal has more than three decimal places?
A1: The process remains the same. Simply multiply by 100 and add the percentage symbol. For example, 0.1255 x 100 = 12.55%.
Q2: Can a percentage be greater than 100%?
A2: Yes, absolutely. A percentage greater than 100% indicates a value that is more than the whole. For example, 150% represents 1.5 times the whole.
Q3: How do I convert a fraction directly to a percentage?
A3: To convert a fraction to a percentage, divide the numerator by the denominator and then multiply by 100 and add the percentage symbol. For instance, 3/4 = 0.75, and 0.75 x 100 = 75%.
Q4: Why is understanding this conversion important?
A4: This conversion is fundamental to understanding and working with proportions, ratios, and relative quantities. It's vital in various fields, including finance, statistics, science, and everyday life.
Conclusion
Converting 0.125 to a percentage, which equals 12.5%, is a simple yet crucial mathematical operation. This guide has not only provided the solution but also explored the underlying principles, connecting decimals, fractions, and percentages. Understanding these conversions empowers you to tackle various real-world problems and confidently navigate numerical information across different disciplines. The ability to effortlessly switch between these representations is a powerful tool for anyone seeking to strengthen their mathematical skills and improve their understanding of quantitative data. Remember, practice makes perfect, so try converting other decimals to percentages to solidify your understanding.
Latest Posts
Latest Posts
-
20 Of 199
Sep 22, 2025
-
0 24as A Fraction
Sep 22, 2025
-
Kaethe Kollwitz Artwork
Sep 22, 2025
-
16 3 4
Sep 22, 2025
-
Rhyme Of Dreams
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 0.125 To Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.