3/4 Of 48
interactiveleap
Sep 15, 2025 · 5 min read
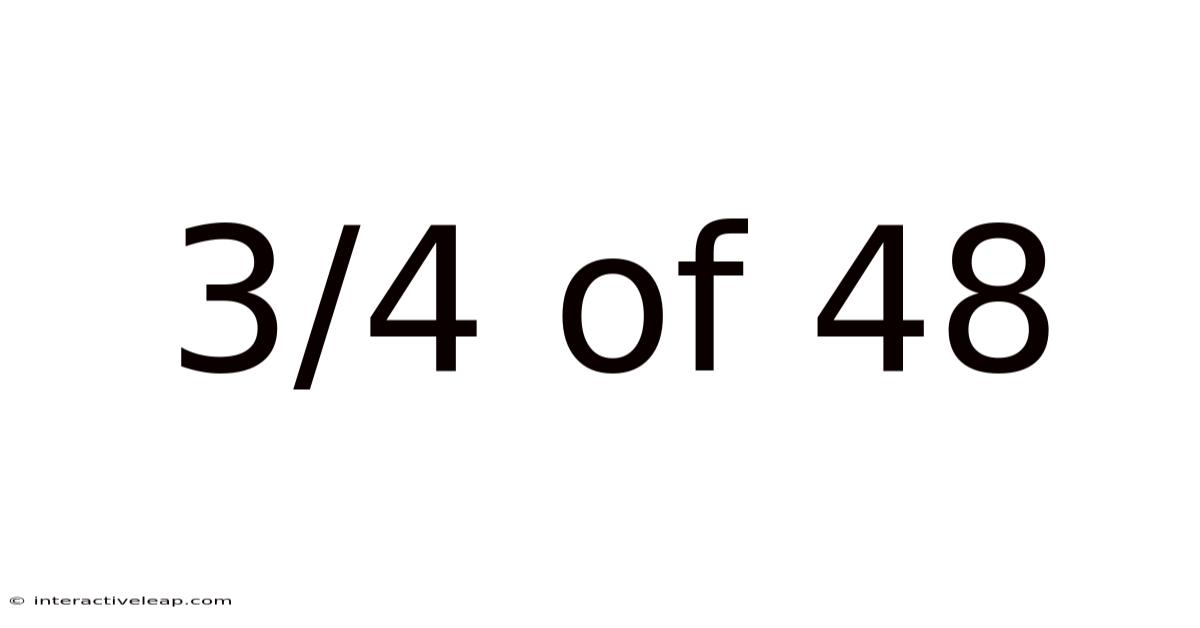
Table of Contents
Unveiling the Mystery: A Deep Dive into 3/4 of 48
Finding 3/4 of 48 might seem like a simple arithmetic problem, suitable only for elementary school students. But beneath the surface of this seemingly straightforward calculation lies a wealth of mathematical concepts and real-world applications that can enrich our understanding of fractions, percentages, and proportions. This article will not only guide you through solving this problem but also explore its underlying principles, providing a comprehensive and engaging learning experience for all levels. We'll delve into different methods of solving the problem, examine the concept of fractions and their relation to percentages, and discuss practical scenarios where understanding this type of calculation becomes crucial.
Understanding Fractions: The Building Blocks of the Problem
Before we tackle 3/4 of 48, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we're considering 3 out of 4 equal parts of a whole.
Understanding fractions is foundational to many areas of mathematics and beyond. From baking recipes (requiring 2/3 cup of sugar) to calculating probabilities (the chance of flipping heads twice in a row), fractions are everywhere. This problem, finding 3/4 of 48, perfectly exemplifies the practical application of fractional calculations.
Method 1: Direct Calculation – The Classic Approach
The most straightforward way to calculate 3/4 of 48 is to use direct multiplication. We can express "of" as multiplication. So, the problem translates to: (3/4) * 48.
To solve this:
-
Convert the whole number to a fraction: We can write 48 as 48/1. This doesn't change its value, but it puts it in a form suitable for fraction multiplication.
-
Multiply the numerators: 3 * 48 = 144
-
Multiply the denominators: 4 * 1 = 4
-
Simplify the resulting fraction: We now have 144/4. Dividing 144 by 4, we get 36.
Therefore, 3/4 of 48 is 36.
Method 2: Finding One-Fourth and Multiplying – A Step-by-Step Approach
This method breaks down the problem into smaller, more manageable steps. It's particularly useful for visualizing the calculation and for those who find direct fraction multiplication challenging.
-
Find one-fourth (1/4) of 48: Divide 48 by 4: 48 / 4 = 12. This represents one-quarter of the whole.
-
Multiply by three: Since we want three quarters, multiply the result from step 1 by 3: 12 * 3 = 36.
Again, we arrive at the answer: 36. This method emphasizes the meaning of the fraction, highlighting the process of finding a fraction of a whole.
Method 3: Converting to Percentages – Connecting Fractions and Percentages
Fractions and percentages are closely related. A percentage is simply a fraction expressed as a part of 100. To use this method:
-
Convert the fraction to a percentage: 3/4 is equivalent to 75% (because 3/4 * 100 = 75).
-
Find 75% of 48: We can do this by multiplying 48 by 0.75 (the decimal equivalent of 75%). 48 * 0.75 = 36.
Once again, the answer is 36. This method demonstrates the interchangeable nature of fractions and percentages, emphasizing their shared ability to represent parts of a whole.
Real-World Applications: Where This Calculation Matters
The seemingly simple calculation of 3/4 of 48 has numerous real-world applications, spanning various fields:
-
Finance: Calculating discounts, interest, or portions of investments often involves fractions and percentages. For example, a 75% discount on a $48 item directly relates to this calculation.
-
Construction and Engineering: Measuring materials, dividing spaces, or scaling blueprints frequently requires precise fractional calculations. Imagine dividing a 48-meter length of wood into four equal parts; finding three of those parts would be analogous to this problem.
-
Cooking and Baking: Recipes often use fractions for precise ingredient measurements. Scaling up or down a recipe requires an understanding of proportional reasoning, as seen in this problem.
-
Data Analysis: Analyzing data often involves calculating percentages or proportions of a whole. Understanding fractions is vital for interpreting these data meaningfully.
Expanding the Concept: Proportions and Ratios
The problem of 3/4 of 48 also elegantly demonstrates the concept of proportions. A proportion is a statement that two ratios are equal. We can express this problem as a proportion:
3/4 = x/48
To solve for x (which represents 3/4 of 48), we can cross-multiply:
4x = 3 * 48
4x = 144
x = 36
This highlights the interconnectedness of fractions, proportions, and ratios, offering a more nuanced understanding of the mathematical concepts at play.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this problem? A: Absolutely! Calculators are excellent tools for verifying your calculations, especially for more complex problems. However, understanding the underlying mathematical principles is crucial for problem-solving proficiency.
-
Q: What if the fraction wasn't 3/4? How would I adapt the methods? A: The methods described above apply to any fraction. Simply replace 3/4 with the desired fraction and follow the same steps.
-
Q: Are there other ways to solve this problem? A: Yes, there are other, more advanced methods involving algebra and other mathematical concepts, but the methods described are the most intuitive and accessible for a broad audience.
-
Q: Why is understanding fractions important? A: Fractions form the foundation of many advanced mathematical concepts. Mastery of fractions is essential for success in algebra, calculus, and other higher-level mathematics.
Conclusion: Beyond the Numbers
While finding 3/4 of 48 might appear to be a simple arithmetic exercise, delving deeper reveals a wealth of interconnected mathematical concepts. This problem serves as a stepping stone to a broader understanding of fractions, percentages, proportions, and ratios – concepts vital for success in various academic and professional fields. By exploring different methods of solving this seemingly simple problem, we not only obtain the answer (36) but also strengthen our foundational mathematical skills and appreciate the practical relevance of these core concepts in our everyday lives. Remember, mathematics is not just about numbers; it's about understanding relationships, patterns, and the power of logical reasoning. The journey of understanding 3/4 of 48 is a journey into the heart of mathematical literacy.
Latest Posts
Latest Posts
-
Graph Of 4x
Sep 15, 2025
-
40ml In Oz
Sep 15, 2025
-
78f To C
Sep 15, 2025
-
5 Of 190
Sep 15, 2025
-
5 Of 1000000
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Of 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.