3/4 Of 32
interactiveleap
Sep 14, 2025 · 5 min read
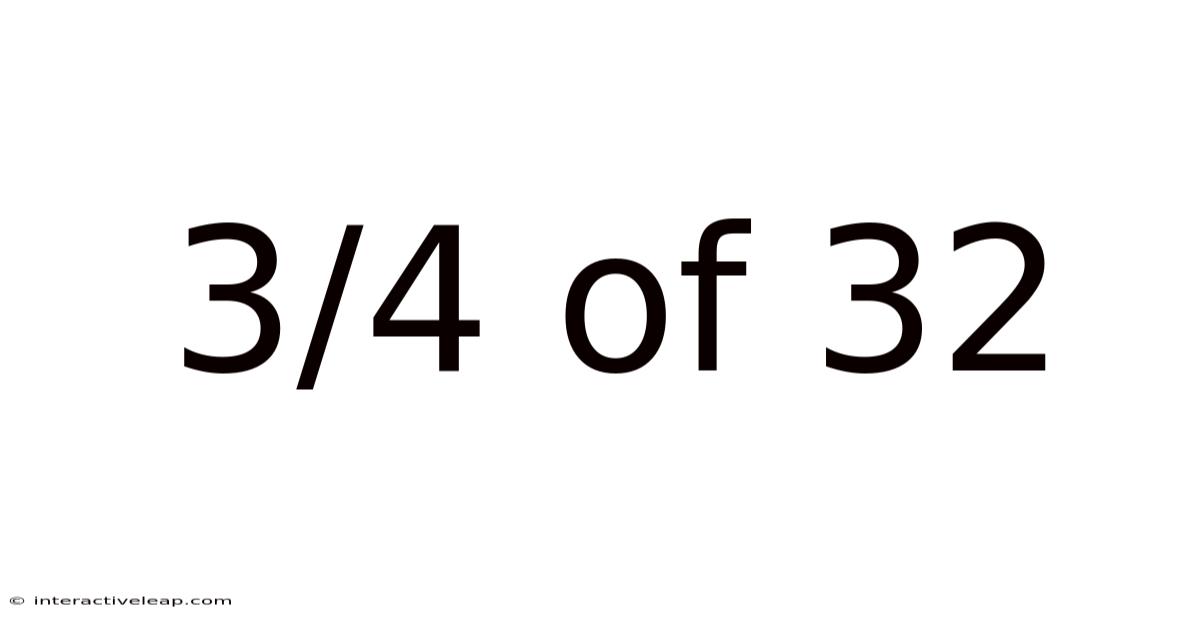
Table of Contents
Decoding 3/4 of 32: A Deep Dive into Fractions and Their Applications
Finding 3/4 of 32 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to solve this seemingly basic calculation unlocks a deeper understanding of fractions, percentages, and their widespread applications in various fields, from everyday budgeting to advanced engineering. This article will not only show you how to calculate 3/4 of 32 but also explore the underlying concepts, providing you with a comprehensive understanding of fractional arithmetic and its real-world significance.
Understanding Fractions: A Foundation for Calculation
Before diving into the calculation of 3/4 of 32, let's establish a solid understanding of what fractions represent. A fraction is a part of a whole. It is expressed as a ratio of two numbers – the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we are considering 3 out of 4 equal parts of a whole.
Calculating 3/4 of 32: Step-by-Step Approach
There are several ways to calculate 3/4 of 32. Here are two common methods:
Method 1: Multiplication
The most straightforward method is to multiply the fraction by the whole number. We can express 32 as a fraction by putting it over 1 (32/1). Therefore, the calculation becomes:
(3/4) * (32/1) = (3 * 32) / (4 * 1) = 96 / 4 = 24
Therefore, 3/4 of 32 is 24.
Method 2: Finding the Fractional Part and Multiplying
This method involves first finding the value of one-fourth (1/4) of 32 and then multiplying that value by 3.
1/4 of 32 = 32 / 4 = 8
Now, multiply this value by 3 to find 3/4:
8 * 3 = 24
This method also confirms that 3/4 of 32 is 24.
Beyond the Calculation: Exploring the Concept of Proportions
The calculation of 3/4 of 32 is fundamentally a proportion problem. Proportions describe the relationship between two ratios. We can represent the problem as:
3/4 = x/32
Where 'x' represents the unknown value (3/4 of 32). To solve for 'x', we can cross-multiply:
4x = 3 * 32
4x = 96
x = 96 / 4
x = 24
This demonstrates how the concept of proportions is intrinsically linked to fractional calculations. Understanding proportions is crucial for solving various mathematical problems and real-world applications.
Real-World Applications of Fractional Calculations
The seemingly simple calculation of 3/4 of 32 has far-reaching implications in many areas:
-
Everyday Budgeting: Imagine you want to save 3/4 of your $32 weekly allowance. Understanding this calculation helps you determine your savings goal ($24).
-
Cooking and Baking: Many recipes utilize fractions. If a recipe calls for 3/4 cup of sugar and you want to double the recipe, you need to calculate 3/4 cup * 2, showcasing the importance of fraction manipulation.
-
Construction and Engineering: Engineers frequently use fractions and proportions in designing structures. Precise measurements and calculations are crucial for the stability and safety of buildings and other constructions.
-
Data Analysis and Statistics: Fractions and percentages are fundamental to interpreting data and drawing conclusions. Understanding how to calculate fractions is essential for various statistical analyses.
-
Discount Calculations: Sales often involve discounts expressed as fractions or percentages. Knowing how to calculate 3/4 of a price allows you to quickly determine the discounted value.
Decimal Equivalents and Percentage Conversions
Fractions can be easily converted to decimals and percentages, providing alternative ways to represent the same value.
To convert 3/4 to a decimal, simply divide the numerator by the denominator:
3 ÷ 4 = 0.75
To convert 0.75 to a percentage, multiply by 100:
0.75 * 100 = 75%
Therefore, 3/4 of 32 is equivalent to 0.75 * 32 = 24, and also 75% of 32 = 24. This demonstrates the interconnectedness of fractions, decimals, and percentages.
Advanced Applications: Fractional Exponents and Calculus
While this article focuses on basic fractional arithmetic, it's important to note that fractions play a significant role in more advanced mathematical concepts. Fractional exponents, for example, represent roots and powers. Calculus, a cornerstone of higher mathematics, utilizes fractions extensively in concepts like derivatives and integrals. Mastering basic fractional calculations forms a solid foundation for understanding these advanced topics.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to find 3/4 of 32?
- A: Yes, you can. Most calculators have a fraction function or can easily perform the multiplication (3/4) * 32.
-
Q: What if I need to find a different fraction of 32?
- A: The same principles apply. Simply replace 3/4 with your desired fraction and perform the calculation using either multiplication or finding the fractional part.
-
Q: Are there other methods to solve this problem?
- A: Yes, you could use visual aids like diagrams to represent the fraction and the whole number, providing a more intuitive understanding of the calculation.
-
Q: Why is understanding fractions important?
- A: Fractions are fundamental to mathematics and are essential for problem-solving in various fields, ranging from everyday tasks to complex scientific calculations. A strong grasp of fractions is crucial for academic success and real-world applications.
Conclusion: Mastering Fractions for a Brighter Future
Finding 3/4 of 32 might appear trivial at first glance. However, a deeper exploration reveals the rich mathematical concepts underlying this seemingly simple calculation. From understanding fractions and proportions to their widespread applications in diverse fields, mastering fractional arithmetic is not merely about solving equations but about developing a fundamental skill set that will benefit you throughout your life. The ability to confidently tackle fractional calculations empowers you to solve real-world problems, make informed decisions, and achieve a more profound understanding of the world around you. So, embrace the power of fractions – they're more than just numbers; they're the building blocks of mathematical understanding and practical problem-solving.
Latest Posts
Latest Posts
-
6x 4 Factorise
Sep 14, 2025
-
25 Of 3500
Sep 14, 2025
-
52 5kg In Stones
Sep 14, 2025
-
33lbs In Kg
Sep 14, 2025
-
49 6kg In Stone
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.