6x 4 Factorise
interactiveleap
Sep 14, 2025 · 6 min read
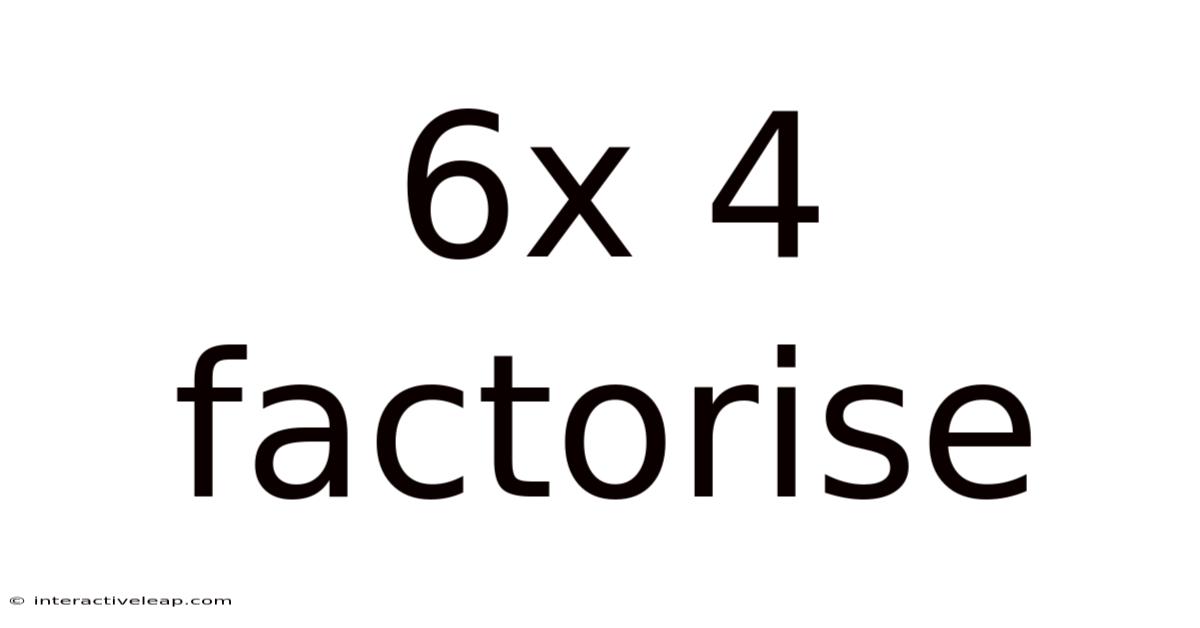
Table of Contents
Mastering the 6x4 Factorisation Technique: A Comprehensive Guide
Factoring expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding more advanced mathematical concepts. While simple factorisations are relatively straightforward, more complex expressions require a deeper understanding of techniques. This comprehensive guide delves into the intricacies of 6x4 factorisation, a method frequently encountered in higher-level algebra, providing a step-by-step approach accessible to all learners. This article will cover various strategies, explain the underlying mathematical principles, and address common questions to ensure a thorough understanding of this crucial algebraic skill.
Understanding the Basics: What is Factorisation?
Before we dive into the specifics of 6x4 factorisation, let's establish a solid foundation. Factorisation, also known as factoring, is the process of breaking down an expression into simpler components that, when multiplied together, yield the original expression. Think of it like reverse multiplication. For example, factoring the expression 6x + 12 involves finding two expressions that, when multiplied, result in 6x + 12. In this case, the factors are 6 and (x + 2) because 6(x + 2) = 6x + 12.
This process is essential because it simplifies complex expressions, making them easier to manipulate and solve. It's a crucial step in solving quadratic equations, simplifying rational expressions, and understanding a wide range of other algebraic concepts.
Approaching 6x4 Factorisation: Strategies and Techniques
The term "6x4 factorisation" isn't a formally defined algebraic technique. It likely refers to factorising expressions involving six terms (often polynomials of degree 5 or higher) and potentially requiring four factors or groupings to achieve complete factorisation. There's no single, universally applicable algorithm for this, but rather a combination of strategies based on pattern recognition and algebraic manipulation. Here's a breakdown of common approaches:
1. Grouping: The Foundation of 6x4 Factorisation
Grouping is a fundamental strategy for factoring polynomials with many terms. It involves strategically grouping terms that share common factors. Let's illustrate this with an example:
Consider the expression: x⁵ + 2x⁴ + 3x³ + 6x² + x + 2
We can group terms as follows:
(x⁵ + 2x⁴) + (3x³ + 6x²) + (x + 2)
Now, factor out the greatest common factor (GCF) from each group:
x⁴(x + 2) + 3x²(x + 2) + 1(x + 2)
Notice that (x + 2) is a common factor across all three terms. We can factor it out:
(x + 2)(x⁴ + 3x² + 1)
This simplified the expression considerably. The resulting expression might be further factorable, depending on the nature of the remaining polynomial. This often requires techniques for factoring quadratics or other higher-degree polynomials.
2. Factor Theorem and Synthetic Division
For polynomials of higher degrees, the Factor Theorem and synthetic division can be invaluable tools. The Factor Theorem states that if P(x) is a polynomial and P(a) = 0, then (x - a) is a factor of P(x). This means if substituting a specific value of x results in zero, the expression is divisible by (x - a).
Synthetic division provides an efficient method for dividing a polynomial by a linear factor. Let's say we suspect (x + 1) is a factor of a six-term polynomial. Synthetic division allows us to quickly determine the quotient and check if the remainder is zero, confirming our suspicion.
3. Recognising Patterns and Special Cases
Some six-term expressions might exhibit patterns that allow for efficient factoring. These patterns often involve sums or differences of cubes, perfect squares, or other recognizable algebraic structures. Careful observation and recognition of these patterns can greatly simplify the process.
4. Iterative Factoring
Sometimes, complete factorisation requires a multi-step process. You might initially group and factor, resulting in a simpler expression that can be further factored using other techniques, such as quadratic factoring or difference of squares. This iterative approach is common when dealing with complex polynomials.
Illustrative Examples: Working Through 6x4 Factorisation Problems
Let's tackle a few examples to solidify our understanding.
Example 1:
Factor the expression: 2x⁵ + 4x⁴ - 2x³ - 4x² + x + 2
- Grouping: (2x⁵ + 4x⁴) + (-2x³ - 4x²) + (x + 2)
- Factoring GCF: 2x⁴(x + 2) - 2x²(x + 2) + 1(x + 2)
- Common Factor: (x + 2)(2x⁴ - 2x² + 1)
The remaining quadratic expression (2x⁴ - 2x² + 1) might not factor further using real numbers, depending on the discriminant.
Example 2:
Factor the expression: x⁶ - 1
This is a difference of squares (x³)² - 1². It factors as:
(x³ - 1)(x³ + 1)
Each of these factors can be factored further using the difference and sum of cubes formulas, respectively:
(x - 1)(x² + x + 1)(x + 1)(x² - x + 1)
This example demonstrates how recognizing patterns can significantly simplify the factorisation process.
Advanced Techniques and Considerations
-
Cubic and Quartic Formulae: For certain higher-degree polynomials, formulae exist to find roots (and hence factors) though these are often complex and computationally intensive.
-
Numerical Methods: For polynomials that don't factor easily using algebraic methods, numerical methods can be used to approximate the roots.
-
Computer Algebra Systems (CAS): Software like Mathematica or Maple can be used to factor complex polynomials.
Frequently Asked Questions (FAQ)
Q: Is there a single "6x4 factorisation" method?
A: No, "6x4 factorisation" isn't a specific technique. It refers to the challenge of factorising expressions with six terms, potentially resulting in four factors. The approach involves a combination of strategies like grouping, factoring by parts, and potentially using more advanced techniques.
Q: What if I can't find a common factor after grouping?
A: If grouping doesn't immediately reveal a common factor, try rearranging the terms in different orders before concluding that another method is needed. Consider using the Factor Theorem and synthetic division to test for potential factors.
Q: How do I know when an expression is fully factorised?
A: An expression is fully factorised when it cannot be broken down further into simpler expressions using real or complex number coefficients. The factors should ideally be linear expressions (degree 1) or irreducible quadratic expressions (degree 2 with no real roots).
Conclusion: Mastering the Art of Factorisation
Factorising expressions is a fundamental algebraic skill that builds upon itself. While simple factorisations might seem straightforward, tackling more complex problems, like those implicitly suggested by “6x4 factorisation,” requires a combination of techniques, strategic thinking, and pattern recognition. This comprehensive guide provides a solid foundation for approaching these challenges, building confidence and competence in algebraic manipulation. Remember, practice is key. The more you work through diverse examples, the more adept you will become at recognizing patterns, applying appropriate strategies, and mastering the art of factorisation. Don't be afraid to experiment, and with persistence, you'll be tackling even the most intricate algebraic expressions with ease.
Latest Posts
Latest Posts
-
50 Meters Yards
Sep 14, 2025
-
1 78m In Ft
Sep 14, 2025
-
23 Multiplication Table
Sep 14, 2025
-
10 Of 64
Sep 14, 2025
-
5 7 Of 134
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 6x 4 Factorise . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.