3 4 13
interactiveleap
Sep 18, 2025 · 7 min read
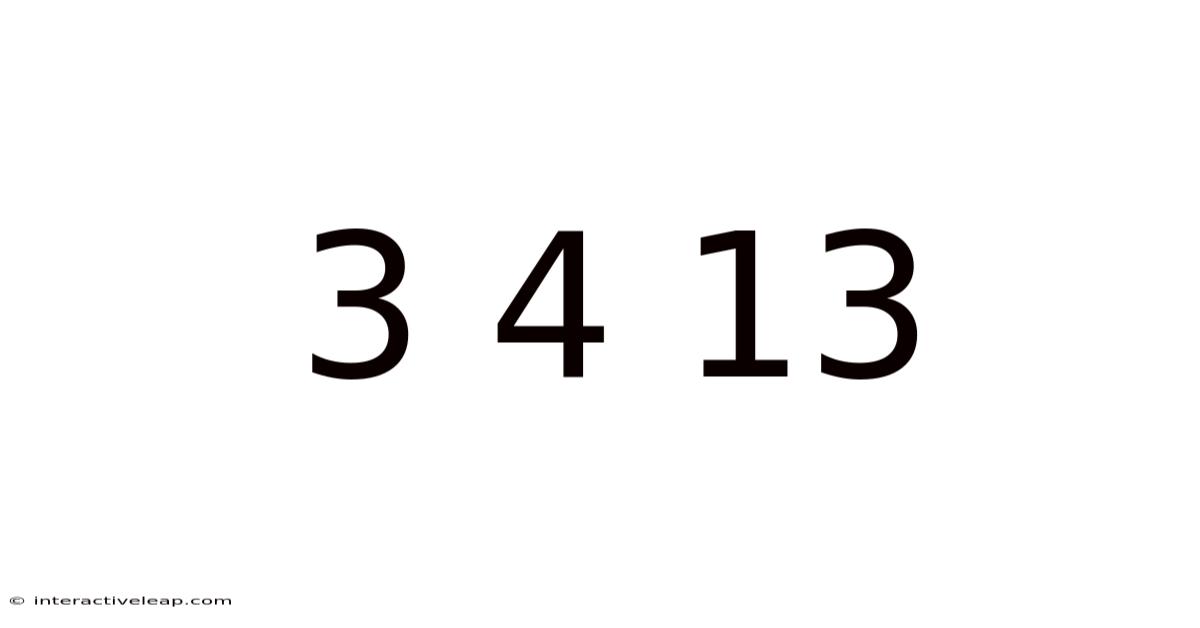
Table of Contents
Unlocking the Mysteries of 3, 4, and 13: A Deep Dive into Number Theory, Combinatorics, and More
The seemingly simple numbers 3, 4, and 13 hold a wealth of mathematical significance, far exceeding their initial impression. This exploration delves into the fascinating properties of these numbers, examining their roles in various mathematical fields, including number theory, combinatorics, geometry, and even their surprising appearances in nature and culture. We'll uncover their interconnectedness and reveal the hidden depths behind their seemingly ordinary nature.
I. Introduction: The Significance of Simple Numbers
Numbers, the fundamental building blocks of mathematics, often reveal surprising complexity upon closer inspection. While 3, 4, and 13 might appear unremarkable at first glance, a deeper investigation unveils a rich tapestry of mathematical properties and applications. This article will not only define these numbers within various mathematical contexts but also demonstrate their interconnectedness and illustrate how their seemingly simple properties contribute to more complex mathematical concepts. We will uncover their roles in prime factorization, modular arithmetic, combinatorics, and geometrical constructions, shedding light on their pervasive influence in the mathematical world.
II. Number Theory: Prime Numbers, Divisibility, and Beyond
-
3: A Prime Number with Unique Properties: 3 is the second smallest prime number, meaning it's only divisible by 1 and itself. Prime numbers are foundational in number theory, forming the building blocks of all integers through prime factorization. 3's unique position in the sequence of prime numbers gives it significance in various mathematical theorems and algorithms. Furthermore, 3 possesses unique properties related to modular arithmetic, which are crucial in cryptography and other computational applications.
-
4: A Composite Number with Square Properties: In contrast to 3, 4 is a composite number – meaning it has more than two divisors (1, 2, and 4). Its significance lies in its property as a perfect square (2²), leading to various geometrical and algebraic implications. The number 4 is heavily involved in quadratic equations and the study of perfect squares and higher powers.
-
13: A Prime Number with Significance in Modular Arithmetic: 13 is another prime number, holding a different set of properties compared to 3. Its prime nature is essential in number theory, specifically in modular arithmetic. Modular arithmetic, where numbers "wrap around" after reaching a certain value (the modulus), is crucial in cryptography and coding theory. 13's prime nature ensures certain computational advantages and cryptographic strengths. For instance, 13 is used in various congruency relations and as a base for modular exponentiation.
III. Combinatorics and Counting: Permutations, Combinations, and More
The numbers 3, 4, and 13 play significant roles in combinatorics, the study of counting and arrangements.
-
3: Triangular Numbers and Permutations: 3 is a triangular number (1+2=3), which relates to geometric arrangements and combinatorial problems involving triangular patterns. The number of permutations (arrangements) of 3 distinct objects is 3! (3 factorial) = 6. This forms the basis for more complex combinatorial calculations.
-
4: Tetrahedral Numbers and Combinations: 4 relates to tetrahedral numbers (a 3-dimensional extension of triangular numbers) and appears in various combinatorial problems related to arranging objects in three dimensions. The number of combinations of choosing 2 objects from a set of 4 is given by the binomial coefficient ₄C₂ = 6, illustrating its role in selection problems.
-
13: Combinations and the Lottery: The number 13 frequently appears in lottery calculations. Consider the number of possible combinations in a lottery involving selecting 6 numbers from a set of 13. This calculation uses combinations, a core concept in combinatorics. The sheer magnitude of possibilities reveals the low probability of winning such lotteries.
IV. Geometry and Spatial Relationships
-
3: Triangles and the Fundamental Shape: 3 is the minimum number of sides needed to form a polygon (a triangle). Triangles are fundamental in geometry, forming the basis for many other shapes and constructions. Their properties, such as the Pythagorean theorem for right-angled triangles, are essential in various geometric proofs and applications.
-
4: Squares and Cubes: 4 is the number of sides in a square, a fundamental geometric shape. Extending this to three dimensions, 4 also relates to the number of faces of a tetrahedron (a 3-dimensional pyramid) and the number of vertices of a cube. This demonstrates its connection to spatial relationships in three-dimensional geometry.
-
13: Polygons and Tessellations: While less directly connected to fundamental shapes like 3 and 4, 13 still plays a role in the study of polygons. The geometry of 13-sided polygons (tridecagons) has its own unique properties and challenges in terms of constructing regular and irregular shapes. Moreover, the exploration of tessellations (tiling patterns) might involve using polygons with 13 sides as part of more complex designs.
V. Appearances in Other Fields: From Physics to Culture
The numbers 3, 4, and 13 have also found their way into various aspects of our world beyond purely mathematical contexts:
-
3: The Trinity in Religion and Philosophy: The number 3 holds significant symbolic meaning in many religions and philosophical systems, often representing a trinity or triad (e.g., father, son, and holy spirit in Christianity). This highlights the cultural and symbolic significance that numbers can acquire beyond their mathematical properties.
-
4: The Four Elements and Directions: In various cultures and belief systems, the number 4 symbolizes the four elements (earth, air, fire, water) or the four cardinal directions (north, south, east, west). These associations showcase how numbers can become ingrained in cultural narratives and beliefs.
-
13: Triskaidekaphobia (Fear of the Number 13): The number 13 is often associated with bad luck or superstition, leading to the phobia known as triskaidekaphobia. This cultural phenomenon highlights the influence of numbers on human psychology and behavior.
VI. Interconnectedness: Exploring the Relationships Between 3, 4, and 13
While seemingly disparate, 3, 4, and 13 exhibit subtle interconnectedness within the broader landscape of mathematics. For instance:
-
Pythagorean Triples: While not directly involving 13, the concept of Pythagorean triples (sets of three integers that satisfy the Pythagorean theorem, a² + b² = c²) highlights the relationship between 3 and 4. The simplest Pythagorean triple is (3, 4, 5), illustrating a fundamental relationship between these numbers in geometry and number theory.
-
Modular Arithmetic and Prime Numbers: Both 3 and 13 are prime numbers, leading to similar properties in modular arithmetic. Their prime nature allows for certain computations and cryptographic applications that wouldn't be possible with composite numbers.
VII. Advanced Concepts and Further Exploration
The exploration of 3, 4, and 13 can extend to more advanced mathematical concepts:
-
Higher-Dimensional Geometry: The numbers 4 and 13 can be examined within the context of higher-dimensional geometry, exploring their roles in constructing higher-dimensional shapes and polytopes.
-
Number Theory Theorems: Advanced number theory theorems often involve prime numbers like 3 and 13, leading to complex relationships and proofs within the field.
-
Abstract Algebra: The properties of 3, 4, and 13 can be studied within the framework of abstract algebra, exploring their behavior under different algebraic structures and operations.
VIII. Frequently Asked Questions (FAQ)
-
Q: Are 3, 4, and 13 related in any specific mathematical formula?
- A: While there isn't one single overarching formula relating 3, 4, and 13 directly, they appear in various distinct mathematical contexts. Their interrelation becomes apparent when examining their individual properties within broader mathematical frameworks like number theory, combinatorics, and geometry. The simplest Pythagorean triple (3, 4, 5) shows a connection between 3 and 4 within the Pythagorean theorem.
-
Q: What is the significance of these numbers in cryptography?
- A: 3 and 13, being prime numbers, are important in cryptography, specifically in modular arithmetic-based algorithms. Their prime nature ensures certain computational advantages and enhances the security of cryptographic systems.
-
Q: Are there any unsolved problems related to these numbers?
- A: While 3, 4, and 13 themselves aren't directly connected to major unsolved problems, the areas of mathematics they represent (prime numbers, combinatorics, geometry) contain numerous open questions and unsolved problems that continue to challenge mathematicians.
IX. Conclusion: The Enduring Significance of Simple Numbers
The exploration of 3, 4, and 13 reveals the profound depths within seemingly simple numbers. Their roles in number theory, combinatorics, geometry, and even culture highlight the interconnectedness of mathematics and its pervasiveness in various aspects of our world. This deep dive demonstrates that even seemingly ordinary numbers can hold a wealth of mathematical significance, inspiring further investigation and appreciation for the beauty and complexity inherent in the mathematical world. The journey into the properties and applications of these three numbers showcases the rich tapestry of mathematical concepts and their profound impact on our understanding of the universe.
Latest Posts
Latest Posts
-
Ethnicity Definition Sociology
Sep 18, 2025
-
11 3 4
Sep 18, 2025
-
Torr To Pascal
Sep 18, 2025
-
1 66m In Feet
Sep 18, 2025
-
5 Of 220
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 3 4 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.