3/20 As Decimal
interactiveleap
Sep 20, 2025 · 6 min read
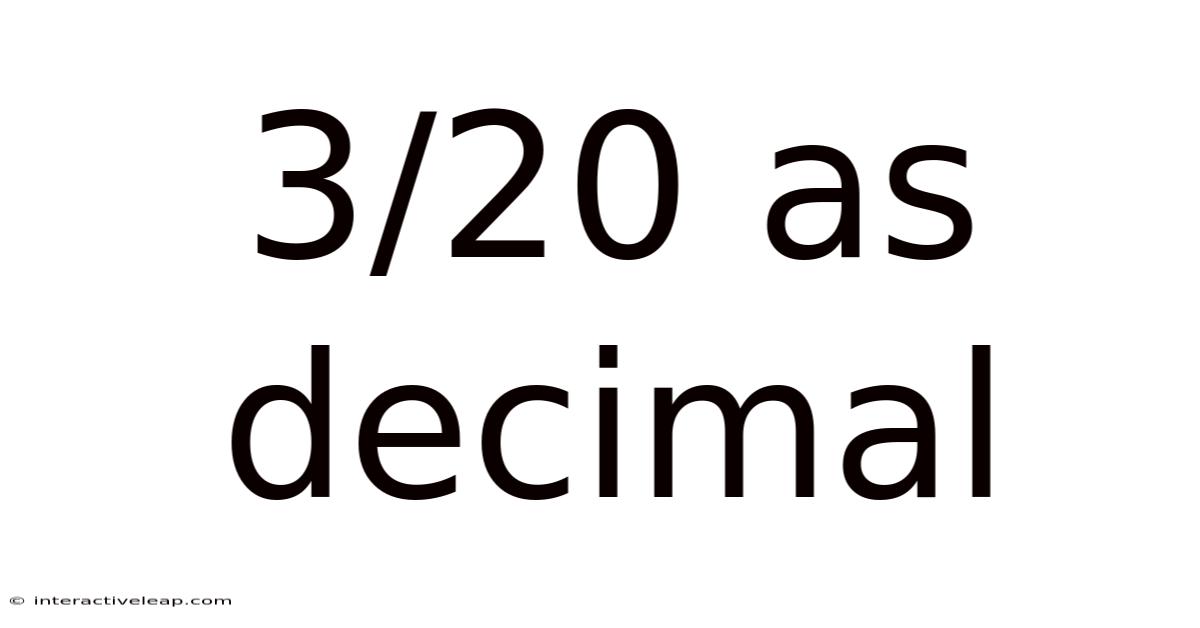
Table of Contents
Decoding 3/20 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is fundamental to mathematics and numerous real-world applications. This article delves deep into converting the fraction 3/20 into its decimal form, exploring various methods, underlying principles, and practical applications. We'll move beyond a simple answer and equip you with a robust understanding of fraction-to-decimal conversion, ensuring you can tackle similar problems with confidence.
Introduction: Understanding Fractions and Decimals
Before diving into the conversion of 3/20, let's establish a firm understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 3/20, 3 is the numerator and 20 is the denominator. This means we're considering 3 out of 20 equal parts.
A decimal, on the other hand, represents a number based on the power of 10. It uses a decimal point to separate the whole number part from the fractional part. For instance, 0.5 represents half (or 1/2), and 0.75 represents three-quarters (or 3/4). Decimals are incredibly useful for expressing parts of a whole in a concise and easily comparable format.
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. We simply divide the numerator by the denominator. In this case:
3 ÷ 20 = ?
Performing this division, we get:
3 ÷ 20 = 0.15
Therefore, 3/20 as a decimal is 0.15. This method is easily applicable using a calculator or by performing long division manually. Long division provides a deeper understanding of the process, showing how the fraction is broken down into tenths, hundredths, and so on.
Method 2: Equivalent Fractions and Decimal Conversion
Another approach involves creating an equivalent fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000, etc.). This makes the conversion to a decimal much simpler.
To achieve this with 3/20, we need to find a number that, when multiplied by 20, results in a power of 10. Since 20 is 2 x 10, multiplying both the numerator and denominator by 5 will achieve this:
(3 x 5) / (20 x 5) = 15/100
Now, converting 15/100 to a decimal is straightforward. The denominator, 100, represents hundredths. Therefore, 15/100 is equivalent to 0.15. This method reinforces the understanding of fraction equivalence and demonstrates the flexibility in representing the same value in different forms.
Method 3: Understanding Place Value
Understanding decimal place value is crucial in comprehending decimal representations. Each place to the right of the decimal point represents a decreasing power of 10:
- Tenths: 1/10 = 0.1
- Hundredths: 1/100 = 0.01
- Thousandths: 1/1000 = 0.001
- and so on...
When we have 15/100, we can directly place the 15 in the hundredths place, resulting in 0.15. This emphasizes the relationship between the denominator of the fraction and the place value in the decimal representation.
Illustrative Examples: Expanding the Understanding
Let's expand our understanding by exploring similar fraction-to-decimal conversions. This will reinforce the techniques discussed above and demonstrate their applicability to a broader range of fractions:
- 1/4: Dividing 1 by 4 gives 0.25. Alternatively, we can create an equivalent fraction: (1 x 25) / (4 x 25) = 25/100 = 0.25.
- 2/5: Dividing 2 by 5 gives 0.4. Creating an equivalent fraction: (2 x 2) / (5 x 2) = 4/10 = 0.4
- 7/8: This requires long division or creating an equivalent fraction with a denominator that is a power of 10. Dividing 7 by 8 gives 0.875. This example highlights that not all fractions result in terminating decimals (decimals that end); some result in repeating decimals (decimals with a repeating sequence of digits).
Practical Applications: Where Decimals Shine
The conversion of fractions to decimals isn't just an academic exercise; it has significant practical applications across various fields:
- Finance: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals. For example, a 15% discount is equivalent to 0.15.
- Measurement: Many measurement systems utilize decimals, such as the metric system (kilometers, meters, centimeters). Converting fractional measurements to decimals ensures consistency and ease of calculation.
- Engineering and Science: Precise calculations in engineering and scientific fields frequently require decimal representations for accuracy and efficiency.
- Data Analysis: Working with data often involves using decimals to represent proportions, ratios, and statistical measures.
Beyond 3/20: Tackling More Complex Fractions
While 3/20 is a relatively straightforward fraction to convert, the principles discussed here are applicable to more complex fractions. For fractions with larger numerators and denominators, long division or a calculator is often the most efficient method. However, understanding the underlying concepts of fraction equivalence and decimal place value remains crucial for comprehending the results.
Frequently Asked Questions (FAQ)
Q: What if the fraction results in a repeating decimal?
A: Some fractions, when converted to decimals, result in a non-terminating, repeating decimal. For instance, 1/3 equals 0.333... In these cases, you can either round the decimal to a specific number of decimal places or represent it using a bar notation (e.g., 0.3̅) to indicate the repeating digit.
Q: Can all fractions be converted to decimals?
A: Yes, all fractions can be converted to decimals through division. The result might be a terminating decimal (ending after a finite number of digits) or a repeating decimal (having a repeating sequence of digits).
Q: Why are decimals preferred in certain applications?
A: Decimals offer advantages in several situations, such as easier comparison, calculation, and representation in digital systems compared to fractions. Decimals are often preferred in applications requiring precise measurements and calculations.
Q: Is there a quicker method than long division for converting fractions to decimals?
A: While long division is a fundamental method, calculators and software tools can significantly speed up the conversion process, especially for more complex fractions. However, understanding the process behind long division remains crucial for grasping the underlying principles.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions to decimals is a fundamental skill with far-reaching applications. This article has explored multiple approaches to converting 3/20 to its decimal equivalent (0.15), emphasizing the underlying principles of fractions, decimals, and place value. By understanding these principles, you can confidently convert any fraction to its decimal representation, enhancing your mathematical skills and expanding your capabilities across various fields. Remember that while calculators can simplify the process, a thorough understanding of the underlying concepts ensures a deeper and more meaningful grasp of mathematical principles. Practice makes perfect, so continue to explore different fractions and consolidate your understanding.
Latest Posts
Latest Posts
-
German Romantic Opera
Sep 20, 2025
-
8 5 X 4
Sep 20, 2025
-
Well Hello Hello
Sep 20, 2025
-
Horizontal Progressive Evacuation
Sep 20, 2025
-
25 Of 225
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3/20 As Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.