2x 5 12
interactiveleap
Sep 19, 2025 · 6 min read
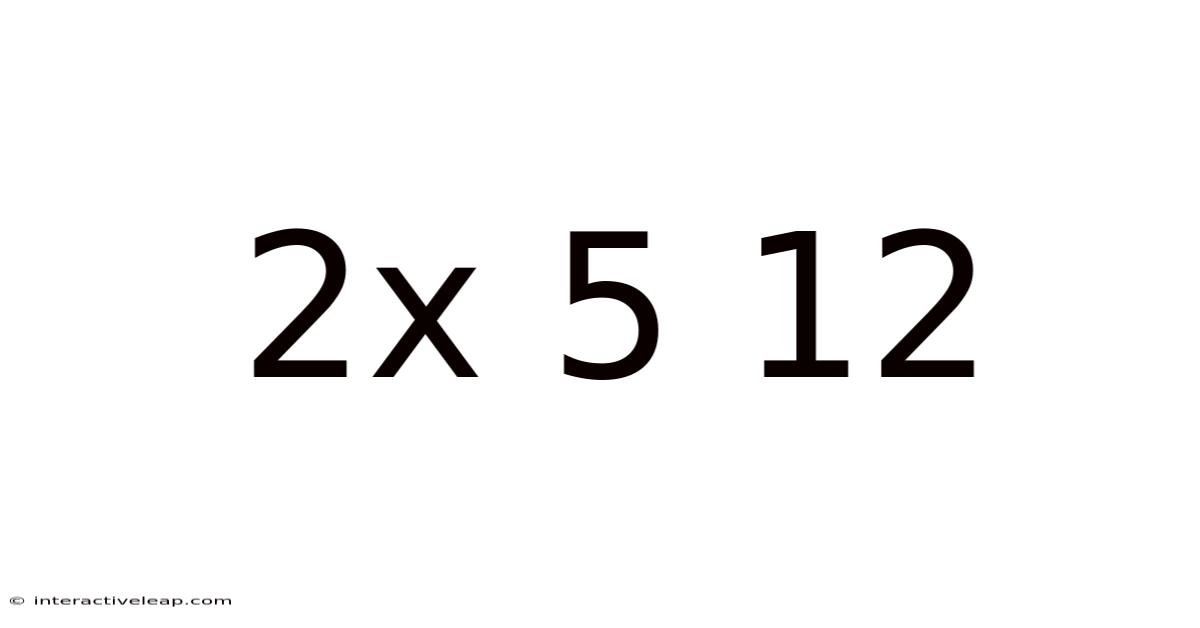
Table of Contents
Decoding 2x5x12: A Deep Dive into the World of Matrix Multiplication and its Applications
The seemingly simple expression "2x5x12" might initially appear mundane. However, within the realm of linear algebra, this notation hints at a powerful concept: matrix multiplication. Understanding 2x5x12, and the broader topic of matrix operations, opens doors to solving complex problems across diverse fields, from computer graphics and machine learning to quantum physics and economics. This article will explore the meaning of 2x5x12 in the context of matrices, delve into the mechanics of matrix multiplication, and uncover its far-reaching applications.
Understanding Matrix Dimensions
Before we tackle 2x5x12, let's establish a foundation. A matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. The dimensions of a matrix are denoted as m x n, where 'm' represents the number of rows and 'n' represents the number of columns. For example, a 2x3 matrix has 2 rows and 3 columns.
In our case, "2x5x12" doesn't represent a single matrix, but rather the dimensions of three matrices involved in a series of multiplications. Let's break it down:
- 2x5: This represents a matrix with 2 rows and 5 columns. We can call this matrix A.
- 5x12: This represents a matrix with 5 rows and 12 columns. We can call this matrix B.
- The implied 2x12: The product of matrix A (2x5) and matrix B (5x12) results in a new matrix with dimensions 2x12. This is because matrix multiplication rules dictate that the inner dimensions must match (in this case, the 5 in both matrices), and the resulting matrix takes the outer dimensions (2 and 12).
The Mechanics of Matrix Multiplication
Matrix multiplication isn't simply element-wise multiplication. It involves a more intricate process:
-
Compatibility: For matrix multiplication to be possible, the number of columns in the first matrix must equal the number of rows in the second matrix. This is crucial. If the inner dimensions don't match, the multiplication is undefined.
-
The Dot Product: The core of matrix multiplication lies in the dot product. The dot product of two vectors (a row from the first matrix and a column from the second matrix) is calculated by multiplying corresponding elements and then summing the results.
-
Building the Resulting Matrix: Each element in the resulting matrix is obtained by taking the dot product of a row from the first matrix and a column from the second matrix.
Let's illustrate with a smaller example:
Matrix A (2x3):
[ 1 2 3 ]
[ 4 5 6 ]
Matrix B (3x2):
[ 7 8 ]
[ 9 10]
[11 12]
To find the element in the first row and first column of the resulting matrix (let's call it C), we take the dot product of the first row of A and the first column of B:
(17) + (29) + (3*11) = 7 + 18 + 33 = 58
This becomes the element C(1,1). We repeat this process for each element in the resulting matrix C (2x2):
[ 58 64 ]
[139 154 ]
This is a simplified example. Multiplying a 2x5 matrix by a 5x12 matrix would involve significantly more calculations, but the underlying principle remains the same.
2x5x12 in the Real World: Applications and Examples
The ability to perform matrix multiplication is fundamental to numerous applications across various disciplines. Here are some key examples:
-
Computer Graphics: Matrix transformations are essential for manipulating 3D models. Rotation, scaling, and translation of objects in a 3D space are all represented by matrices, and the resulting transformations are calculated using matrix multiplication. Imagine a video game; every object movement, camera angle, and lighting effect is heavily reliant on these computations.
-
Machine Learning: Matrix multiplication forms the backbone of many machine learning algorithms. In neural networks, for example, the propagation of information through layers involves multiplying weight matrices by input vectors. The sheer volume of calculations makes efficient matrix multiplication libraries crucial for training sophisticated models.
-
Image Processing: Image manipulation techniques, such as image filtering and compression, often utilize matrices to represent images and apply transformations. Consider image sharpening or blurring; these effects are achieved through matrix operations.
-
Economics and Finance: Matrix algebra is used extensively in econometrics to model economic systems and analyze financial data. Input-output models, which describe the interdependencies between different sectors of an economy, are often represented and analyzed using matrix multiplication.
-
Physics and Engineering: Matrix methods are employed in solving systems of linear equations, which appear frequently in physics and engineering problems. For example, analyzing circuits, structural mechanics, or quantum systems often involves solving large sets of linear equations via matrix techniques.
-
Data Analysis and Statistics: Large datasets are often represented as matrices. Matrix operations are used for various statistical computations, such as principal component analysis (PCA) and regression analysis. PCA, for instance, uses matrix decomposition to reduce the dimensionality of data while preserving important information.
Computational Considerations: Efficiency and Optimization
Performing matrix multiplication for large matrices can be computationally expensive. The number of operations grows rapidly with the size of the matrices. The naive approach has a time complexity of O(n³), where n is the size of the matrix. However, significant advancements have been made in developing efficient algorithms for matrix multiplication, such as Strassen's algorithm, which achieves a lower time complexity. These optimizations are critical for handling the massive matrices encountered in machine learning and other computationally intensive applications.
Frequently Asked Questions (FAQ)
-
Q: What if the inner dimensions don't match in matrix multiplication?
- A: The multiplication is undefined. You cannot multiply two matrices if the number of columns in the first matrix is not equal to the number of rows in the second matrix.
-
Q: Is matrix multiplication commutative?
- A: No, matrix multiplication is generally not commutative. This means that A x B is usually not equal to B x A. Even if both multiplications are defined, the resulting matrices will typically have different dimensions and values.
-
Q: Are there any specialized libraries for matrix operations?
- A: Yes, numerous libraries are available in various programming languages that provide optimized functions for matrix multiplication and other linear algebra operations. Examples include NumPy (Python), Eigen (C++), and MATLAB's built-in functions.
-
Q: What is the significance of the "transpose" of a matrix?
- A: The transpose of a matrix is obtained by swapping its rows and columns. It plays a crucial role in many matrix operations and is frequently used in various applications, including calculating inner products and solving linear equations.
Conclusion: The Power of 2x5x12 and Beyond
While "2x5x12" might seem like a simple sequence of numbers, it unveils the elegant power and widespread applicability of matrix multiplication. Understanding this fundamental concept is key to grasping the intricate workings of numerous algorithms and models across diverse fields. From the vibrant world of computer graphics to the complexities of machine learning and the precision of scientific modeling, the ability to perform and interpret matrix multiplication remains a cornerstone of modern computation and analysis. Mastering this mathematical tool equips individuals with the skills to tackle complex problems and innovate in various fields, driving advancements across technology, science, and beyond. The seemingly simple 2x5x12 opens a vast landscape of computational possibilities.
Latest Posts
Latest Posts
-
Neutron Relative Charge
Sep 19, 2025
-
Loom For Beads
Sep 19, 2025
-
80 Of 34
Sep 19, 2025
-
Weight Tracker Graph
Sep 19, 2025
-
Square Root 21
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2x 5 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.