25 Of 250
interactiveleap
Sep 22, 2025 · 6 min read
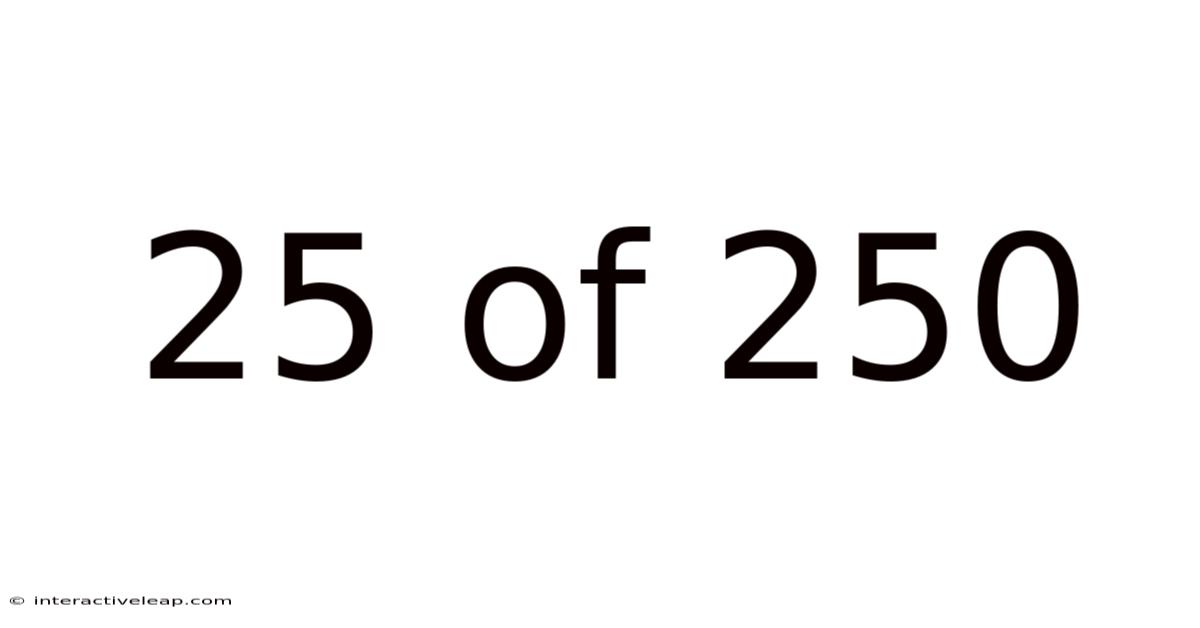
Table of Contents
Decoding 25 of 250: Understanding Proportions and Percentages
The seemingly simple phrase "25 of 250" holds a wealth of information, far beyond its literal meaning. Understanding how to interpret this kind of statement is crucial in various contexts, from everyday calculations to complex statistical analysis. This article will explore the meaning of "25 of 250," delving into the underlying concepts of proportions, percentages, ratios, and their applications in different fields. We'll unpack the calculations, demonstrate practical examples, and address frequently asked questions to provide a comprehensive understanding of this fundamental mathematical concept.
What Does "25 of 250" Mean?
At its most basic, "25 of 250" means that there are 25 items out of a total of 250 items. This represents a part of a whole. This seemingly simple statement forms the basis for numerous calculations and analyses. The key is understanding how to express this relationship quantitatively, allowing for comparisons and interpretations.
Calculating the Proportion
The first step in analyzing "25 of 250" is calculating the proportion. A proportion is a fraction representing the relationship between the part and the whole. In this case, the proportion is:
25/250
This fraction can be simplified by dividing both the numerator (25) and the denominator (250) by their greatest common divisor, which is 25:
25 ÷ 25 / 250 ÷ 25 = 1/10
This simplified fraction, 1/10, means that 25 represents one-tenth of 250. This proportion provides a concise representation of the relationship between the two numbers.
Converting to Percentage
Proportions are often expressed as percentages for easier understanding and comparison. To convert the proportion 1/10 into a percentage, we multiply it by 100%:
(1/10) * 100% = 10%
Therefore, 25 out of 250 represents 10%. This percentage clearly shows that 25 constitutes 10% of the total 250. This is a particularly useful way to represent the data when comparing different sets of numbers or making inferences about the overall composition of a group.
Understanding Ratios
While proportions focus on the relationship between a part and a whole, ratios compare the relationship between two or more quantities. In this case, the ratio of the part (25) to the whole (250) can be expressed as:
25:250
Similar to proportions, this ratio can be simplified by dividing both numbers by their greatest common divisor (25):
25 ÷ 25 : 250 ÷ 25 = 1:10
This simplified ratio, 1:10, indicates that for every one item in the smaller quantity, there are ten items in the larger quantity. Ratios are particularly useful when comparing different proportions or when the focus is on the relative sizes of two or more quantities.
Practical Applications of "25 of 250"
The principles of proportions, percentages, and ratios derived from "25 of 250" have widespread applications across various fields. Let's explore a few examples:
-
Business and Finance: Imagine a company with 250 employees, and 25 of them received a promotion. The 10% promotion rate can be used to analyze employee performance, evaluate promotion strategies, and make predictions about future promotions.
-
Education: If a class of 250 students took a test, and 25 scored above 90%, the 10% representing the top performers can inform teaching methods, identify areas needing improvement, and track student progress.
-
Science and Research: In scientific experiments, if 25 out of 250 samples tested positive for a particular substance, the 10% positive rate provides crucial data for analysis, conclusions, and further research directions. This could be used in fields such as medicine, environmental science, or material science.
-
Polling and Surveys: If 25 out of 250 people surveyed favored a particular political candidate, the 10% approval rating is a critical piece of information for campaign strategies, media analysis, and election forecasting.
-
Quality Control: In manufacturing, if 25 out of 250 items produced were defective, the 10% defect rate helps identify quality control issues, optimize production processes, and manage risk.
Beyond the Basics: More Complex Scenarios
The "25 of 250" example is a fundamental illustration of proportional reasoning. However, real-world problems often involve more intricate scenarios. Consider these extensions:
-
Comparing Proportions: Imagine another group with 150 individuals, and 10 received a promotion. This represents a proportion of 10/150, which simplifies to 1/15 or approximately 6.7%. Comparing this 6.7% to the initial 10% allows for insightful comparisons between the two groups.
-
Combining Proportions: If two subgroups within the initial 250 individuals are considered, say 100 with 5 promotions (5%) and 150 with 20 promotions (13.3%), a weighted average can be calculated to understand the overall proportion.
-
Predictive Modeling: The 10% rate observed in the "25 of 250" scenario could be used to predict future outcomes. For example, if the total number increases to 500, a simple extrapolation might suggest that approximately 50 individuals would fall into the same category (although this is a simplification and more robust statistical methods might be needed for accuracy).
Frequently Asked Questions (FAQ)
Q: How do I calculate the percentage increase or decrease if the number changes from 25 to, say, 30?
A: To calculate the percentage increase, first find the difference: 30 - 25 = 5. Then divide the difference by the original value and multiply by 100%: (5/25) * 100% = 20%. This indicates a 20% increase. Percentage decrease is calculated similarly, using the same formula but focusing on the decrease.
Q: What if I have more than two numbers involved in a proportional relationship?
A: Proportions and ratios can easily extend to more than two numbers. For example, if you have 25 red apples, 50 green apples, and 175 yellow apples out of a total of 250 apples, you can calculate the proportion of each color and express them as percentages.
Q: Are there any software tools that can help with these calculations?
A: Many software programs, including spreadsheets (like Microsoft Excel or Google Sheets), statistical software packages (like SPSS or R), and even simple calculators can perform these calculations easily. Spreadsheets are particularly useful for larger datasets and more complex analyses.
Q: What are some common mistakes people make when working with proportions and percentages?
A: Common mistakes include incorrectly identifying the part and the whole, misinterpreting fractions and decimals, and not simplifying ratios and proportions. Careful attention to detail and a thorough understanding of the underlying concepts are crucial to avoid errors.
Conclusion: Mastering the Power of Proportions
The seemingly straightforward phrase "25 of 250" offers a gateway to a deeper understanding of proportions, percentages, and ratios. Mastering these concepts is not only essential for mathematical proficiency but also for navigating various aspects of daily life, professional endeavors, and academic pursuits. By understanding how to calculate and interpret these relationships, we can effectively analyze data, make informed decisions, and gain valuable insights from seemingly simple numerical information. The ability to confidently work with proportions and percentages opens doors to a broader understanding of the world around us and empowers us to make sense of the quantitative information we encounter daily.
Latest Posts
Latest Posts
-
2 X 3x
Sep 22, 2025
-
28divided By 3
Sep 22, 2025
-
Itp Vs Ttp
Sep 22, 2025
-
10 X 365
Sep 22, 2025
-
40 Divide 3
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.