24divided By 3
interactiveleap
Sep 15, 2025 · 5 min read
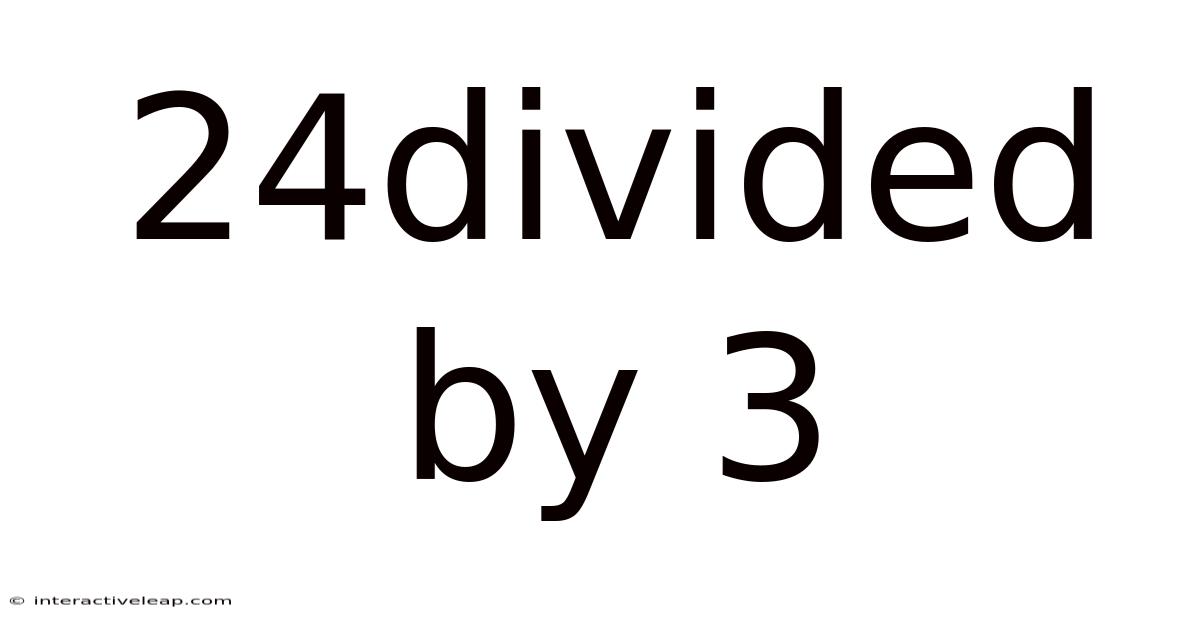
Table of Contents
Unveiling the Simplicity and Power of 24 Divided by 3: A Deep Dive into Division
This article explores the seemingly simple calculation of 24 divided by 3, going far beyond the basic answer. We'll delve into the fundamental principles of division, explore different methods of solving this problem, and uncover the broader mathematical concepts it represents. Understanding this seemingly basic operation provides a foundation for more complex mathematical concepts and problem-solving skills. We'll cover various approaches, including repeated subtraction, using multiplication facts, visual representations, and connecting it to real-world applications. This comprehensive guide aims to solidify your understanding of division and demonstrate its practical relevance.
Introduction: Understanding Division
Division, one of the four basic arithmetic operations, is essentially the process of splitting a quantity into equal parts. The expression "24 divided by 3" asks: "If we have 24 items, and we want to divide them into 3 equal groups, how many items will be in each group?" The answer, as most know, is 8. But how do we arrive at this answer, and what does it mean within a broader mathematical context?
Methods for Solving 24 Divided by 3
Several methods can effectively solve this division problem. Let's explore some of them:
1. Repeated Subtraction:
This is a foundational method, particularly helpful for visualizing division. We repeatedly subtract the divisor (3) from the dividend (24) until we reach zero. Each subtraction represents one group.
- 24 - 3 = 21
- 21 - 3 = 18
- 18 - 3 = 15
- 15 - 3 = 12
- 12 - 3 = 9
- 9 - 3 = 6
- 6 - 3 = 3
- 3 - 3 = 0
We subtracted 3 eight times before reaching zero. Therefore, 24 divided by 3 equals 8. This method clearly demonstrates the concept of splitting 24 into equal groups of 3.
2. Multiplication Facts:
This method leverages the inverse relationship between multiplication and division. We ask ourselves: "What number, when multiplied by 3, equals 24?" Knowing our multiplication tables, we quickly recall that 3 x 8 = 24. Therefore, 24 ÷ 3 = 8. This method is efficient and relies on memorized multiplication facts.
3. Long Division:
While perhaps overkill for such a simple problem, long division offers a structured approach applicable to more complex divisions.
8
3 | 24
-24
0
We ask how many times 3 goes into 2 (it doesn't), so we consider how many times 3 goes into 24. It goes in 8 times (3 x 8 = 24). Subtracting 24 from 24 leaves a remainder of 0. This confirms our answer of 8.
4. Visual Representation:
Visual aids can make division more intuitive, especially for younger learners. Imagine 24 objects (e.g., apples) arranged in 3 equal rows. Counting the number of objects in each row reveals the answer: 8. This method reinforces the concept of equal sharing. You can also use arrays or diagrams to represent this visually. For example, a 3 x 8 array of dots would clearly represent the 24 items divided into 3 groups of 8.
Beyond the Answer: Exploring Deeper Mathematical Concepts
The simple calculation 24 ÷ 3 = 8 provides a springboard for understanding several key mathematical concepts:
-
Factors and Multiples: 3 and 8 are factors of 24, meaning they divide 24 without leaving a remainder. 24 is a multiple of both 3 and 8. Understanding factors and multiples is crucial in simplifying fractions, finding greatest common divisors (GCD), and least common multiples (LCM).
-
Inverse Operations: Division and multiplication are inverse operations. This means they "undo" each other. If you divide 24 by 3, you get 8. If you multiply 8 by 3, you get back to 24. This inverse relationship is fundamental in solving equations and manipulating algebraic expressions.
-
Remainders: While 24 divided by 3 has no remainder, many division problems do. Understanding remainders is essential in solving real-world problems involving sharing, grouping, and measurement. For instance, if we had 25 apples and wanted to divide them into 3 equal groups, we would have 8 apples in each group and 1 apple remaining.
-
Fractions: Division can be represented as a fraction. 24 ÷ 3 can be written as 24/3, which simplifies to 8. This connection highlights the relationship between division and fractions, a crucial concept in algebra and higher mathematics.
Real-World Applications of Division
Division is far from an abstract mathematical concept; it's a crucial tool for numerous real-world applications. Here are a few examples:
-
Sharing Equally: Dividing a pizza among friends, sharing candy amongst siblings, or splitting the cost of a bill amongst diners are all common scenarios involving division.
-
Measurement and Conversion: Converting units of measurement (e.g., inches to feet, kilometers to miles) often requires division.
-
Averages: Calculating the average of a set of numbers involves summing the numbers and dividing by the count of numbers. This is used extensively in statistics and data analysis.
-
Rates and Ratios: Understanding rates (like miles per hour) and ratios (like the ratio of boys to girls in a class) involves division.
-
Geometry and Area: Calculating the area of a rectangle involves multiplying length and width, while finding the side length of a square given its area requires division.
Frequently Asked Questions (FAQ)
-
What if I don't know my multiplication tables? Repeated subtraction is a viable alternative. You can also use a calculator or refer to multiplication charts.
-
Why is division important? Division is a fundamental skill essential for various real-world applications and further mathematical learning.
-
Are there different types of division? Yes, there's long division (for larger numbers), short division (a quicker method for smaller numbers), and division with remainders.
-
How can I improve my division skills? Practice regularly using different methods, work through problems of increasing difficulty, and utilize online resources or tutoring if needed.
Conclusion: Mastering Division – A Building Block for Success
The seemingly straightforward calculation of 24 divided by 3 reveals a wealth of mathematical understanding and practical applications. Mastering division is not merely about finding the correct answer; it's about grasping the underlying concepts, developing problem-solving skills, and equipping oneself with a tool essential for navigating various aspects of life, from everyday tasks to more advanced mathematical pursuits. This simple operation lays the groundwork for more complex mathematical concepts encountered throughout education and beyond. By exploring various methods and understanding its real-world implications, we can truly appreciate the power and versatility of this fundamental arithmetic operation. So, the next time you encounter a division problem, remember that it's not just about numbers; it's about unlocking a deeper understanding of the world around you.
Latest Posts
Latest Posts
-
64 1 3
Sep 15, 2025
-
24 X 6
Sep 15, 2025
-
20 Of 14000
Sep 15, 2025
-
300 Of 5
Sep 15, 2025
-
7 8km In Miles
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 24divided By 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.