23 X 3
interactiveleap
Sep 16, 2025 · 6 min read
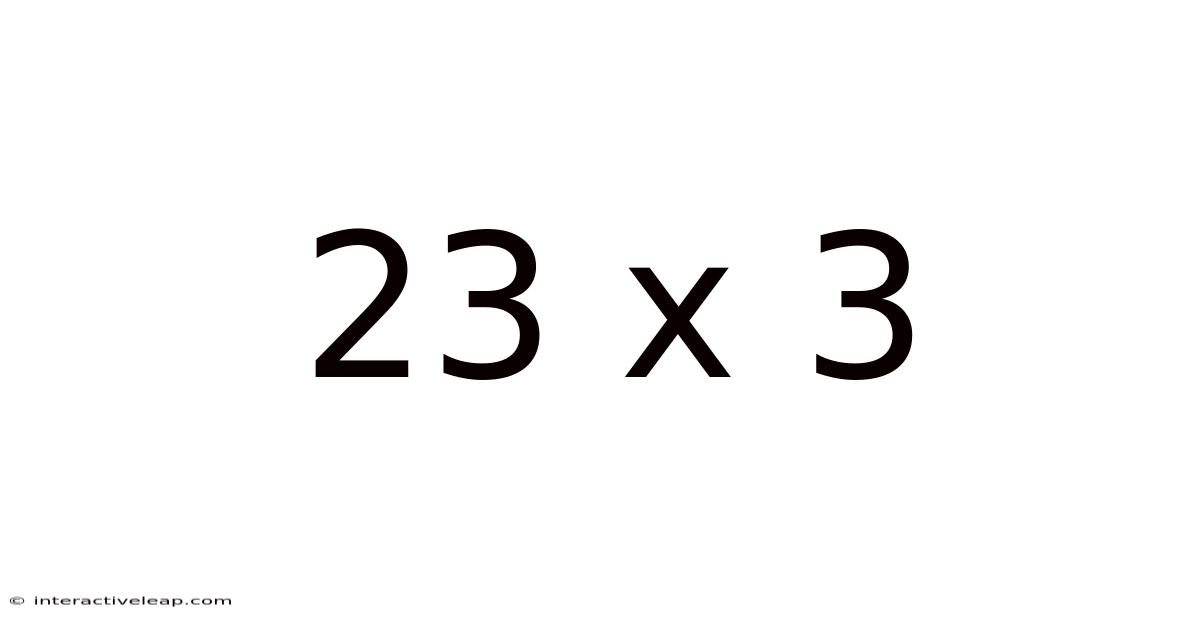
Table of Contents
Decoding 23 x 3: A Deep Dive into Multiplication and Beyond
This article explores the seemingly simple multiplication problem, 23 x 3, as a gateway to understanding fundamental mathematical concepts. We'll move beyond the basic answer to delve into different methods of solving it, the underlying principles of multiplication, its applications in real-world scenarios, and even touch upon related mathematical ideas. This detailed exploration aims to provide a comprehensive understanding of this seemingly simple calculation, making it valuable for students, educators, and anyone curious about the beauty of mathematics.
Understanding the Fundamentals: What is Multiplication?
Multiplication, at its core, is repeated addition. When we say 23 x 3, we're essentially asking: what is the sum of three 23s? This can be visualized as three groups of 23 objects each. Understanding this fundamental concept is crucial before tackling more complex multiplication problems. It lays the groundwork for grasping the logic behind the process.
Methods for Solving 23 x 3
There are several ways to approach solving 23 x 3. Each method offers a unique perspective and helps solidify the understanding of multiplication.
1. Repeated Addition: This is the most straightforward approach. We simply add 23 three times: 23 + 23 + 23 = 69. This method is particularly helpful for visualizing the concept of multiplication as repeated addition, especially for younger learners.
2. Traditional Multiplication (Long Multiplication): This method involves breaking down the numbers into tens and ones and multiplying them separately before adding the results.
- Multiply the ones: 3 x 3 = 9
- Multiply the tens: 3 x 20 = 60
- Add the results: 60 + 9 = 69
This method is highly systematic and provides a clear breakdown of the calculation. It's a foundational method taught in elementary schools and forms the basis for multiplying larger numbers.
3. Distributive Property: This method leverages the distributive property of multiplication over addition. We can rewrite 23 as (20 + 3) and then distribute the 3:
3 x (20 + 3) = (3 x 20) + (3 x 3) = 60 + 9 = 69
This approach highlights the connection between multiplication and addition, demonstrating how multiplication can be broken down into smaller, more manageable parts.
4. Mental Math Techniques: With practice, 23 x 3 can be solved mentally. One technique involves doubling and adding:
- Double 23: 23 x 2 = 46
- Add 23: 46 + 23 = 69
This method is efficient for mental calculations and helps build number sense. Other mental math strategies might involve breaking down the numbers differently based on personal preferences and familiarity with number patterns.
The Significance of Place Value
Understanding place value is critical in multiplication, especially with multi-digit numbers like 23. The number 23 represents 2 tens and 3 ones. When multiplying 23 by 3, we are essentially multiplying both the tens and the ones digits by 3, then adding the results. This highlights the importance of understanding the positional value of each digit in a number.
Applications of 23 x 3 in Real-World Scenarios
While seemingly simple, 23 x 3, or calculations similar to it, frequently appear in daily life. Consider these examples:
- Grocery Shopping: If apples cost $3 each and you buy 23, the total cost is 23 x 3 = $69.
- Baking: A recipe requires 3 cups of flour per batch, and you need to make 23 batches. You’ll need 23 x 3 = 69 cups of flour.
- Construction: If each row of bricks contains 23 bricks, and you need 3 rows, you'll need 23 x 3 = 69 bricks.
- Travel: If your daily travel expenses are $23 and you travel for 3 days, your total expenses are 23 x 3 = $69.
These real-world applications demonstrate that even the most basic mathematical operations are essential tools in navigating everyday life.
Expanding the Concept: Multiplication with Larger Numbers
The principle used to solve 23 x 3 can be extended to multiplying larger numbers. The same logic of breaking down the numbers into their place values and multiplying individually, then adding the results, applies. This forms the foundation for understanding long multiplication algorithms. Mastering 23 x 3 sets the stage for confidently tackling more complex multiplication problems.
Connecting to Other Mathematical Concepts
The seemingly simple problem 23 x 3 connects to a variety of other mathematical concepts:
- Arithmetic: It's a core concept in arithmetic, which forms the basis of many other mathematical areas.
- Algebra: It can be represented algebraically as 3x = 69, where 'x' represents the unknown number (23). Solving this equation reinforces the relationship between multiplication and its inverse operation, division.
- Geometry: Multiplication plays a crucial role in calculating areas and volumes of geometric shapes. For instance, the area of a rectangle with sides 23 and 3 units would be 23 x 3 = 69 square units.
- Number Theory: Understanding factors and multiples is essential in number theory, and 23 x 3 provides a simple example of finding multiples of a number.
This problem serves as a building block for more advanced mathematical concepts.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to multiply 23 x 3?
A: The easiest way depends on individual preference and skill level. Repeated addition is conceptually simple, while mental math techniques are efficient for quick calculations. Traditional long multiplication offers a systematic approach, especially for larger numbers.
Q: Can I use a calculator to solve 23 x 3?
A: Yes, calculators provide a quick solution. However, understanding the underlying methods is crucial for developing a strong mathematical foundation. Using a calculator should complement, not replace, the understanding of the process.
Q: Why is understanding multiplication important?
A: Multiplication is a fundamental mathematical operation with countless applications in everyday life, from budgeting and cooking to engineering and scientific calculations. It underpins many other mathematical concepts and is a building block for higher-level mathematics.
Q: Are there any tricks to make multiplication easier?
A: Yes, various mental math techniques and strategies can simplify multiplication. Practicing these techniques and understanding number patterns significantly improve calculation speed and accuracy.
Conclusion: More Than Just a Simple Calculation
The seemingly simple problem of 23 x 3 serves as a powerful illustration of fundamental mathematical principles. This detailed exploration goes beyond merely providing the answer (69) to uncover the deeper meaning and significance of this operation. By understanding the different methods of solving this problem and its connections to other mathematical concepts, we gain a richer appreciation for the beauty and practicality of mathematics. The journey from a simple calculation to a deep dive into mathematical concepts underscores the importance of understanding the 'why' behind the 'how' in mathematical problem-solving. This holistic approach fosters a strong mathematical foundation, empowering individuals to tackle more complex challenges with confidence and understanding. The seemingly simple 23 x 3 is, in fact, a gateway to a much wider and fascinating world of mathematical possibilities.
Latest Posts
Latest Posts
-
2 9 Cos 17
Sep 16, 2025
-
1 7km To Miles
Sep 16, 2025
-
15 Of 48
Sep 16, 2025
-
50 X 20
Sep 16, 2025
-
20 Of 200
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 23 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.