216 X 2
interactiveleap
Sep 18, 2025 · 5 min read
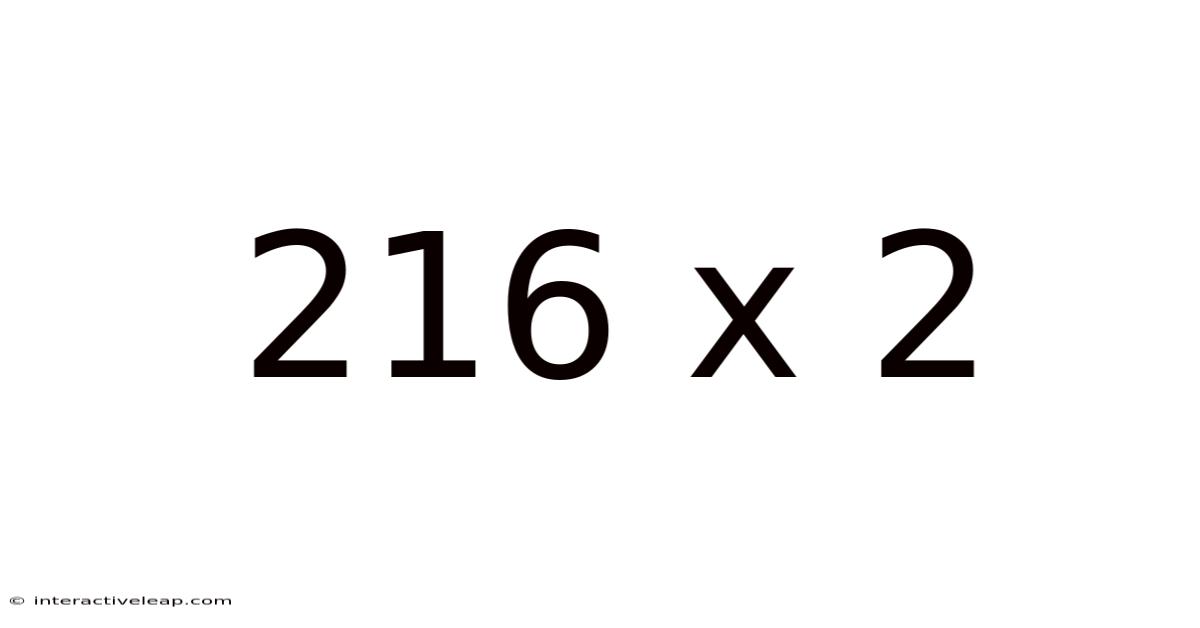
Table of Contents
Decoding 216 x 2: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 216 x 2, expanding beyond the immediate answer to delve into the fundamental principles of multiplication, its various methods, real-world applications, and its significance in broader mathematical contexts. Understanding this seemingly basic equation unlocks a gateway to more complex mathematical concepts. We'll uncover the beauty and power hidden within this seemingly simple problem, making it accessible and engaging for learners of all levels.
Understanding Multiplication: The Basics
Multiplication is a fundamental arithmetic operation representing repeated addition. When we say 216 x 2, we're essentially asking: what is the sum of adding 216 to itself two times? This simple interpretation forms the bedrock of understanding more complex multiplications. We can visually represent this using several methods:
- Repeated Addition: 216 + 216 = 432. This method is excellent for visualizing the concept, especially for younger learners.
- Arrays: Imagine a rectangular array with 216 objects in each row and two rows in total. Counting all the objects gives us the product.
- Number Line: Starting at zero, jump 216 units forward twice. The final position represents the answer.
These visual aids are crucial in building a strong foundational understanding of multiplication before moving on to more abstract methods.
Calculating 216 x 2: Different Approaches
While the repeated addition method works, it can become cumbersome with larger numbers. Let's explore more efficient techniques to solve 216 x 2:
The Standard Algorithm (Column Method)
This is the most common method taught in schools. It involves multiplying each digit of 216 individually by 2, starting from the rightmost digit (ones place), and carrying over any tens or hundreds to the next column.
- Ones Place: 2 x 6 = 12. Write down '2' and carry-over '1'.
- Tens Place: 2 x 1 = 2. Add the carried-over '1': 2 + 1 = 3. Write down '3'.
- Hundreds Place: 2 x 2 = 4. Write down '4'.
Therefore, 216 x 2 = 432.
Distributive Property
The distributive property states that a(b + c) = ab + ac. We can apply this to break down 216 into smaller, more manageable parts:
216 x 2 = (200 + 10 + 6) x 2 = (200 x 2) + (10 x 2) + (6 x 2) = 400 + 20 + 12 = 432
Mental Math Techniques
With practice, you can perform this multiplication mentally. One technique is to double each digit individually:
- Double 200 is 400.
- Double 10 is 20.
- Double 6 is 12.
Adding these results (400 + 20 + 12) gives us 432.
Beyond the Calculation: Exploring Related Concepts
The simple equation 216 x 2 opens doors to a plethora of related mathematical concepts:
Factors and Multiples
In the equation 216 x 2 = 432, 2 and 216 are factors of 432, and 432 is a multiple of both 2 and 216. Understanding factors and multiples is crucial for simplifying fractions, solving equations, and grasping number theory.
Prime Factorization
Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves). Let's find the prime factorization of 432:
432 = 2 x 216 = 2 x 2 x 108 = 2 x 2 x 2 x 54 = 2 x 2 x 2 x 2 x 27 = 2 x 2 x 2 x 2 x 3 x 9 = 2⁴ x 3³
This concept is vital in simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM).
Even and Odd Numbers
216 is an even number (divisible by 2), and multiplying an even number by 2 always results in an even number. Exploring the properties of even and odd numbers leads to understanding number patterns and divisibility rules.
Algebraic Representation
We can represent this multiplication algebraically. Let 'x' represent 216. The equation becomes:
x * 2 = 2x
This simple algebraic expression highlights the power of using variables to represent unknown quantities.
Real-World Applications: Where do we use Multiplication?
Multiplication isn't confined to textbooks; it's an essential tool in various real-world scenarios:
- Shopping: Calculating the total cost of multiple items (e.g., buying two items costing $216 each).
- Cooking: Doubling or tripling recipes.
- Construction: Calculating the amount of materials needed for a project.
- Finance: Calculating interest, calculating earnings based on hourly rates.
- Travel: Determining the total distance traveled over multiple journeys.
- Engineering: Solving problems related to scaling, measurements, and quantities.
Multiplication in Advanced Mathematics
The foundation laid by understanding simple multiplications like 216 x 2 extends to more advanced mathematical concepts:
- Calculus: Multiplication forms the basis of derivatives and integrals.
- Linear Algebra: Matrix multiplication is a cornerstone of linear algebra, used extensively in computer graphics, data analysis, and physics.
- Probability and Statistics: Calculating probabilities often involves multiplication.
Frequently Asked Questions (FAQ)
Q: What is the quickest way to calculate 216 x 2?
A: The quickest method is often mental math, by doubling each digit individually: 400 + 20 + 12 = 432.
Q: Why is understanding multiplication important?
A: Multiplication is a fundamental operation that underpins many aspects of mathematics and its real-world applications. It's crucial for problem-solving, critical thinking, and understanding more complex mathematical concepts.
Q: Are there other ways to visualize 216 x 2?
A: Yes, you can use blocks, counters, or drawings to represent the repeated addition or array methods, making the concept concrete and easier to grasp.
Q: What if I want to multiply 216 by a larger number?
A: The standard algorithm (column method) or the distributive property can be applied to larger numbers. Breaking down the problem into smaller parts makes it more manageable.
Q: How can I improve my multiplication skills?
A: Consistent practice, utilizing different methods, and working through problems of increasing complexity are essential to improve your multiplication skills. Using flashcards, online games, and interactive exercises can also help.
Conclusion
The seemingly simple equation 216 x 2 unveils a wealth of mathematical principles and real-world applications. By exploring different calculation methods, understanding related concepts, and recognizing its importance in various fields, we appreciate the significance of this fundamental operation. Mastering multiplication is not just about finding the answer; it's about developing a deeper understanding of numbers, patterns, and the power of mathematics. This foundational knowledge paves the way for tackling more advanced mathematical concepts and solving real-world problems effectively. So, the next time you encounter a multiplication problem, remember the journey from 216 x 2 and the vast world of mathematics it represents.
Latest Posts
Latest Posts
-
Best Oil Burner
Sep 18, 2025
-
70 Of 20
Sep 18, 2025
-
3 0z Cups
Sep 18, 2025
-
Nicknames For Benjamin
Sep 18, 2025
-
4x 2 X
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 216 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.