2 X2 X2
interactiveleap
Sep 16, 2025 · 6 min read
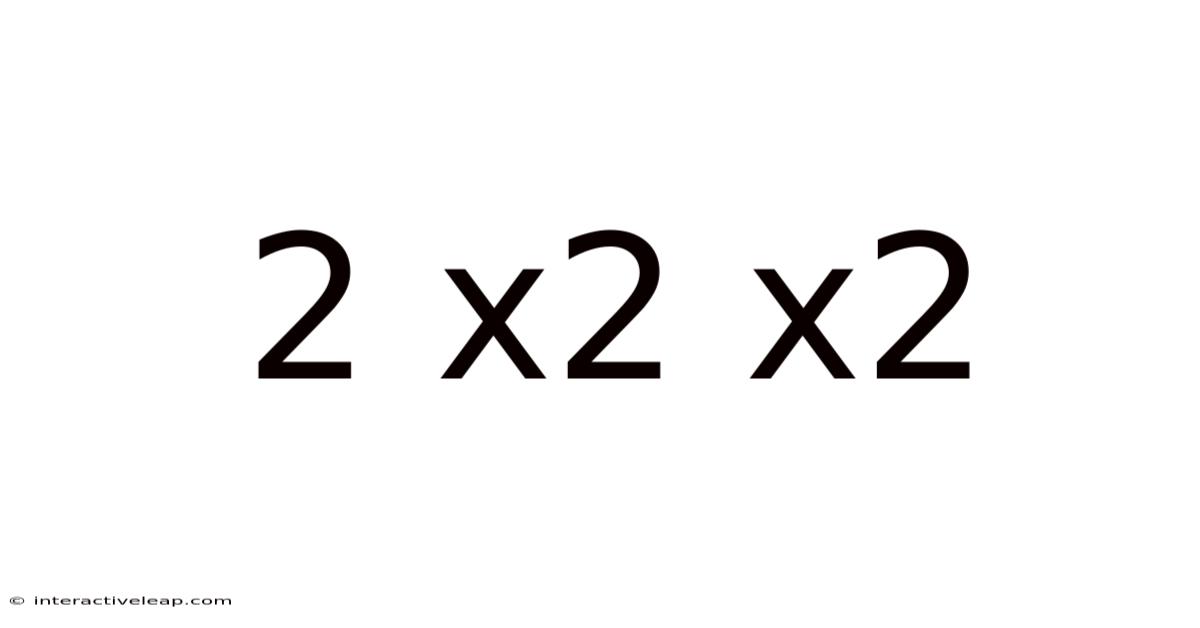
Table of Contents
Decoding 2 x 2 x 2: Exploring the Multifaceted Nature of a Simple Equation
The seemingly simple equation "2 x 2 x 2" might appear trivial at first glance. However, this seemingly straightforward calculation opens doors to a surprisingly rich exploration of mathematical concepts, real-world applications, and even philosophical ponderings about the nature of representation and abstraction. This article will delve into the multifaceted nature of 2 x 2 x 2, going beyond the basic arithmetic to explore its implications across various fields.
The Basic Arithmetic: A Foundation for Understanding
At its core, 2 x 2 x 2 is a multiplication problem. It represents repeated multiplication, where the number 2 is multiplied by itself three times. The order of operations doesn't matter in this case (due to the commutative property of multiplication), so we can solve it in several ways:
- (2 x 2) x 2: First, we multiply 2 by 2, resulting in 4. Then, we multiply 4 by 2, giving us the final answer of 8.
- 2 x (2 x 2): Alternatively, we can first multiply the last two 2s, getting 4, and then multiply that by the first 2, again yielding 8.
This simple calculation yields the answer 8. This seemingly insignificant result is the bedrock upon which we build a deeper understanding of more complex mathematical concepts.
Expanding the Horizons: Beyond Basic Arithmetic
While the immediate answer is 8, the expression "2 x 2 x 2" serves as a springboard for exploring broader mathematical ideas:
-
Exponentiation: The repeated multiplication of 2 can be more concisely expressed as 2³. This introduces the concept of exponentiation, where a base number (2) is raised to a power (3). This notation is crucial for representing large numbers and understanding exponential growth. Understanding 2³ directly links to geometric progressions and the power of compounding, prevalent in finance and various scientific models.
-
Cubic Dimensions: The expression can be visually represented as a cube with sides of length 2 units. This connects the arithmetic operation to geometry. The result, 8, represents the total number of unit cubes that make up the larger cube. This visualization is important in understanding volume calculations and spatial reasoning.
-
Binary System: In the context of computer science, the number 2 plays a fundamental role in the binary system. Binary uses only two digits (0 and 1) to represent all numbers. Understanding how the binary system works provides insight into how computers process and store information. While 2 x 2 x 2 doesn't directly translate to a specific binary manipulation, the repeated multiplication showcases the foundational significance of the number 2 in this system. The number 8 in decimal is 1000 in binary, further highlighting the connection.
-
Set Theory: Consider sets. If you have two sets, each with two elements, and you combine them in every possible way, you get 2 x 2 = 4 combinations. If you add a third set with two elements, the number of total combinations becomes 2 x 2 x 2 = 8. This illustrates the application of this simple equation in combinatorics and probability.
Real-World Applications: From Cubes to Combinations
The seemingly simple 2 x 2 x 2 equation finds itself at the heart of various real-world applications:
-
Volume Calculation: As mentioned earlier, it's directly applicable to calculating the volume of a cube. Imagine a box with dimensions 2 meters x 2 meters x 2 meters. The volume is simply 2 x 2 x 2 = 8 cubic meters. This extends to various fields like construction, engineering, and packaging design.
-
Combinatorial Problems: Consider a scenario with three binary choices (yes/no, on/off, true/false). The total number of possible combinations is 2 x 2 x 2 = 8. This is relevant in computer programming (e.g., setting flags), decision-making processes, and various scenarios involving multiple choices.
-
Exponential Growth: While the equation itself doesn't directly represent exponential growth over time, it highlights the foundational concept of repeated multiplication. Exponential growth models, frequently used in population studies, financial projections, and disease spread analysis, are built upon the principle of repeatedly multiplying a base number.
-
Game Design and Puzzles: Simple puzzles or games often utilize the concept of 2 x 2 x 2 to create different levels or pathways. Consider a game with three switches, each with two states (on/off). The player needs to figure out the correct combination amongst 8 possible states.
Exploring the Philosophical Implications: Abstraction and Representation
Beyond the mathematical and practical applications, 2 x 2 x 2 also sparks philosophical reflection:
-
Abstraction: The equation represents an abstraction of a real-world situation. It strips away the specifics of what is being multiplied and focuses solely on the mathematical operation. This process of abstraction is fundamental to mathematics and allows us to model complex situations using simple tools.
-
Representation: The equation serves as a representation of a physical reality. It can stand for the volume of a cube, the number of combinations, or many other things. The power of mathematics lies in its ability to represent diverse phenomena through abstract symbols and operations.
-
The Nature of Numbers: The equation allows us to ponder the nature of numbers themselves. Are they merely abstract constructs, or do they possess inherent properties independent of human cognition? This simple equation engages a fundamental question about the relationship between mathematics and reality.
Frequently Asked Questions (FAQ)
Q: What is the primary significance of the number 2 in this equation?
A: The number 2 is significant because it's the base number being multiplied. Its repeated multiplication showcases the power of exponential growth and its connection to binary systems prevalent in computer science.
Q: Can this equation be applied to other areas beyond mathematics and science?
A: Yes, the underlying principles of repeated multiplication and combinations extend to various fields such as decision-making, logistics, and even artistic composition.
Q: Is there a more complex way to represent 2 x 2 x 2?
A: Yes, using exponentiation (2³) provides a more concise and mathematically elegant representation. This highlights the efficiency of mathematical notation.
Conclusion: The Enduring Significance of a Simple Equation
While the calculation of 2 x 2 x 2 might seem trivial, its implications extend far beyond a simple arithmetic problem. It serves as a foundation for understanding more complex mathematical concepts, finds application across numerous fields, and prompts deeper philosophical reflection on the nature of abstraction and representation. The seemingly simple equation "2 x 2 x 2 = 8" is a testament to the power and elegance of mathematics – a simple equation unlocking a universe of possibilities. From the geometric representation of a cube to the complexities of binary computation, this equation embodies the core principles of mathematics and showcases its relevance in our world. Its simplicity belies its profound significance, reminding us that even the most basic concepts can have far-reaching implications when explored with curiosity and a thirst for deeper understanding.
Latest Posts
Latest Posts
-
85 Of 480
Sep 16, 2025
-
Factor 2x 10
Sep 16, 2025
-
2 7kg In Lbs
Sep 16, 2025
-
Man In Tophat
Sep 16, 2025
-
Micrometres To Cm
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2 X2 X2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.