192 In Binary
interactiveleap
Sep 23, 2025 · 6 min read
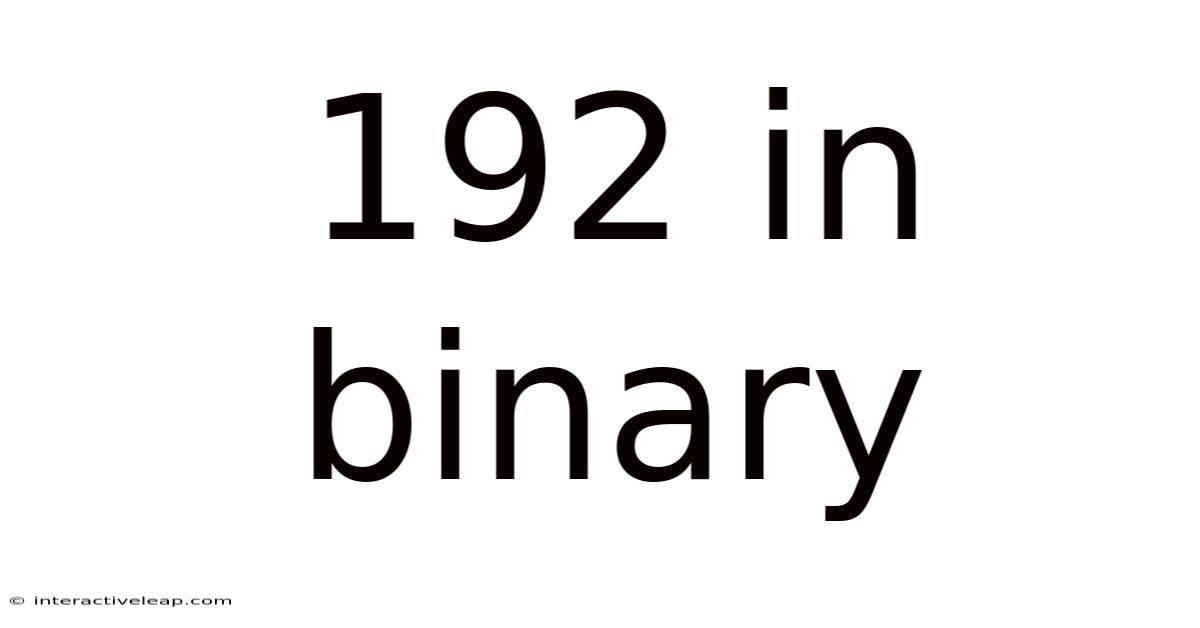
Table of Contents
Decoding 192 in Binary: A Deep Dive into Binary Representation
Understanding binary code is fundamental to comprehending how computers work. This article provides a comprehensive exploration of how the decimal number 192 is represented in binary, explaining the underlying concepts, methods of conversion, and practical applications. We'll delve into the intricacies of the binary system, moving beyond a simple answer to build a solid understanding of this crucial aspect of computer science.
Introduction to Binary Numbers
The decimal number system, the one we use daily, utilizes ten digits (0-9) as its base. In contrast, the binary number system, the language of computers, uses only two digits: 0 and 1. These digits represent the presence (1) or absence (0) of an electrical signal, making it ideal for digital electronics. Each digit in a binary number is called a bit (binary digit). Groups of bits are used to represent larger numbers, characters, and instructions within a computer.
Understanding binary is key to comprehending how computers store and process information, from simple numbers to complex multimedia files. Let's explore how the decimal number 192 is translated into its binary equivalent.
Converting Decimal 192 to Binary: Step-by-Step Guide
There are several methods to convert a decimal number to its binary representation. We'll explore the most common and intuitive approach: the division method.
Method 1: Repeated Division by 2
This method involves repeatedly dividing the decimal number by 2 and recording the remainders. The binary representation is formed by reading the remainders in reverse order.
-
Divide 192 by 2: 192 / 2 = 96 with a remainder of 0.
-
Divide the quotient by 2: 96 / 2 = 48 with a remainder of 0.
-
Continue the process:
- 48 / 2 = 24 with a remainder of 0
- 24 / 2 = 12 with a remainder of 0
- 12 / 2 = 6 with a remainder of 0
- 6 / 2 = 3 with a remainder of 0
- 3 / 2 = 1 with a remainder of 1
- 1 / 2 = 0 with a remainder of 1
-
Read the remainders in reverse order: 11000000.
Therefore, the binary representation of 192 is 11000000.
Method 2: Using Powers of 2
This method involves expressing the decimal number as a sum of powers of 2. We start by identifying the largest power of 2 that is less than or equal to 192.
-
Find the largest power of 2: The powers of 2 are 1, 2, 4, 8, 16, 32, 64, 128, 256, and so on. 128 is the largest power of 2 less than 192.
-
Subtract the power of 2: 192 - 128 = 64
-
Repeat the process: 64 is a power of 2 (2<sup>6</sup>).
-
Represent as a sum: 192 = 128 + 64 = 2<sup>7</sup> + 2<sup>6</sup>
-
Binary Representation: Since 128 is 2<sup>7</sup>, it corresponds to the 8th bit (starting from the rightmost bit, which is 2<sup>0</sup>). Similarly, 64 is 2<sup>6</sup> and corresponds to the 7th bit. All other bits will be 0. This gives us 11000000.
Understanding the Bits and Bytes
The binary number 11000000 consists of eight bits. In computer terminology, eight bits make up one byte. A byte is a fundamental unit of data storage. Many computer systems use a byte as the smallest addressable unit of memory.
Each bit in the byte represents a power of 2, starting from 2<sup>0</sup> (rightmost bit) to 2<sup>7</sup> (leftmost bit). The value of the entire byte is the sum of the powers of 2 corresponding to the bits that are set to 1.
- 11000000 = (1 x 2<sup>7</sup>) + (1 x 2<sup>6</sup>) + (0 x 2<sup>5</sup>) + (0 x 2<sup>4</sup>) + (0 x 2<sup>3</sup>) + (0 x 2<sup>2</sup>) + (0 x 2<sup>1</sup>) + (0 x 2<sup>0</sup>) = 128 + 64 = 192
Binary in Computer Systems: Practical Applications
The binary representation of 192, and indeed all numbers, is crucial to how computers function. Let's examine some practical applications:
-
Data Storage: Computers store all types of data – numbers, text, images, audio, and video – in binary format. Each character, pixel, or sound sample is assigned a unique binary code.
-
Memory Addressing: Computer memory is organized into addressable locations, each identified by a unique binary address. The CPU uses these binary addresses to access and manipulate data in memory.
-
Instruction Sets: Computer programs consist of instructions expressed in binary code (machine code). The CPU decodes these instructions and executes them, performing operations such as arithmetic calculations, data transfers, and logical comparisons.
-
Network Communication: Data transmitted over networks, including the internet, is encoded in binary format. Protocols like TCP/IP use binary to manage data packets and ensure reliable communication.
-
Image Representation: Digital images are composed of pixels, each represented by a binary code that specifies its color and intensity. Higher resolution images require more bits to represent the details.
Binary and Other Number Systems: Hexadecimal and Octal
While binary is fundamental to computers, working directly with long binary strings can be cumbersome. For this reason, other number systems are often used for representing binary data in a more compact form. Two common examples are:
-
Hexadecimal (Base-16): Hexadecimal uses 16 digits (0-9 and A-F) to represent numbers. Each hexadecimal digit corresponds to four bits in binary. This makes it convenient to represent binary data in a more concise way. 192 in hexadecimal is C0.
-
Octal (Base-8): Octal uses eight digits (0-7) and each octal digit corresponds to three bits in binary.
Frequently Asked Questions (FAQ)
- Q: Why do computers use binary?
A: Computers use binary because it's the simplest and most reliable way to represent information using electronic circuits. Each bit can represent either a high voltage (1) or a low voltage (0), making it easy to distinguish between the two states. This binary representation minimizes errors and allows for efficient data processing.
- Q: Can I convert any decimal number to binary?
A: Yes, any decimal number can be converted to binary using the methods described above (repeated division by 2 or using powers of 2).
- Q: What is the significance of the most significant bit (MSB) and the least significant bit (LSB)?
A: The MSB is the leftmost bit in a binary number, representing the highest power of 2. The LSB is the rightmost bit, representing 2<sup>0</sup> (1). The MSB often has special significance, such as representing the sign of a number in signed binary representation.
- Q: How does binary relate to other data types like characters and instructions?
A: Characters and instructions are encoded using binary codes (e.g., ASCII, Unicode for characters; machine code for instructions). Each character or instruction is given a unique binary representation that the computer can understand and process.
Conclusion: The Importance of Binary Understanding
The binary representation of 192 – 11000000 – is more than just a simple conversion; it's a fundamental concept underpinning all digital computing. This article has provided a detailed exploration of how to convert decimal to binary, explained the underlying principles, and highlighted the importance of binary in various aspects of computer systems. A strong grasp of binary numbers is crucial for anyone seeking to understand how computers function at their most basic level. It opens the door to a deeper appreciation of the technology that powers our modern world. From the smallest embedded systems to the largest supercomputers, the language of 0s and 1s remains the cornerstone of computation.
Latest Posts
Latest Posts
-
49 X 12
Sep 23, 2025
-
49 3kg In Stone
Sep 23, 2025
-
Half Eleven Time
Sep 23, 2025
-
Port Udp 137
Sep 23, 2025
-
4cm Into Mm
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 192 In Binary . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.