19 X 3
interactiveleap
Sep 16, 2025 · 6 min read
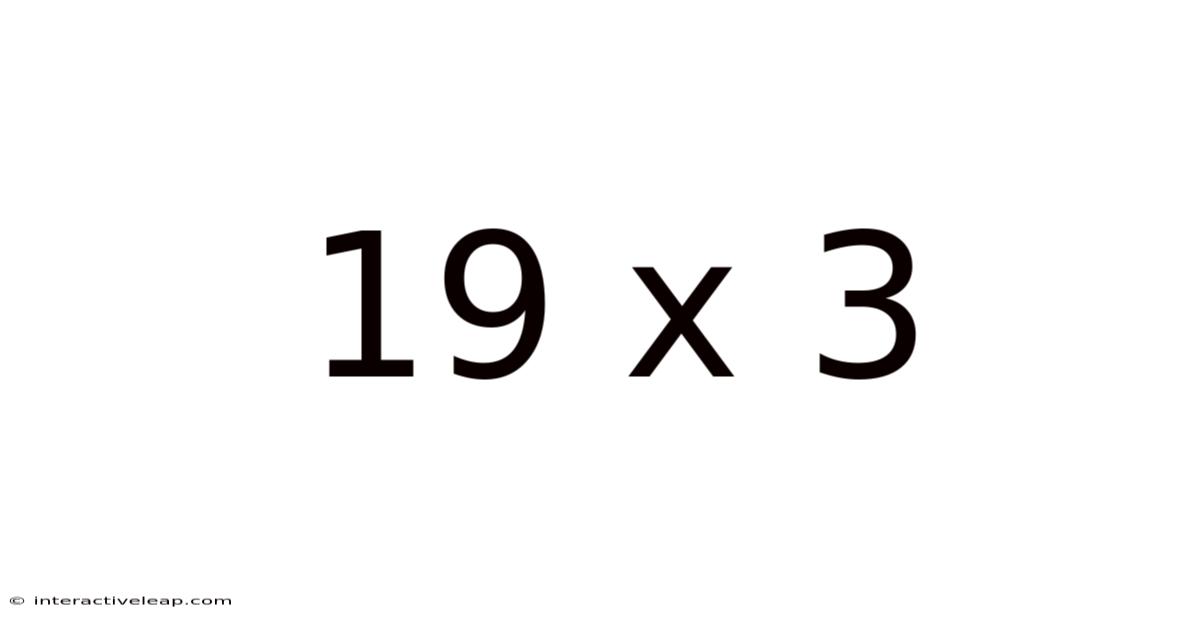
Table of Contents
Unveiling the Mysteries of 19 x 3: A Deep Dive into Multiplication
This article explores the seemingly simple multiplication problem of 19 x 3, delving far beyond the immediate answer. We will unpack various methods for solving this problem, examine the underlying mathematical principles, and explore its applications in real-world scenarios. Understanding this seemingly basic calculation lays a strong foundation for grasping more complex mathematical concepts. We'll also address common misconceptions and frequently asked questions to provide a comprehensive understanding of multiplication and its significance.
Introduction: More Than Just an Answer
At first glance, 19 x 3 appears straightforward. A quick calculation reveals the answer: 57. However, this seemingly simple equation offers a rich opportunity to explore fundamental mathematical concepts and different calculation strategies. This exploration will benefit learners of all ages and skill levels, from elementary school students solidifying their multiplication skills to adults seeking to refresh their understanding of basic arithmetic. This article will demystify the process, highlighting the beauty and logic inherent in even the simplest mathematical operations.
Method 1: Traditional Multiplication
The most common method for solving 19 x 3 involves the traditional algorithm taught in schools. This method breaks down the problem into smaller, manageable steps:
- Multiply the ones digit: 3 x 9 = 27. Write down the '7' and carry-over the '2'.
- Multiply the tens digit: 3 x 1 = 3.
- Add the carry-over: 3 + 2 = 5.
- Combine the results: The final answer is 57.
This method emphasizes place value (ones and tens) and demonstrates the distributive property of multiplication, which we'll explore further in the next section.
Method 2: Distributive Property
The distributive property of multiplication states that a(b + c) = ab + ac. We can apply this principle to solve 19 x 3:
- Break down 19: We can rewrite 19 as (20 - 1).
- Apply the distributive property: 3 x (20 - 1) = (3 x 20) - (3 x 1)
- Perform the multiplications: (3 x 20) = 60 and (3 x 1) = 3.
- Subtract the results: 60 - 3 = 57.
This method demonstrates a more conceptual understanding of multiplication, showcasing how we can manipulate numbers to simplify the calculation. It's a valuable tool for mental math and for solving more complex multiplication problems.
Method 3: Repeated Addition
Multiplication can be understood as repeated addition. 19 x 3 means adding 19 three times:
19 + 19 + 19 = 57
This method is particularly helpful for visualizing multiplication, especially for younger learners who are still developing their understanding of the concept. It reinforces the connection between addition and multiplication.
Method 4: Using Arrays or Grid Method
Visual learners often find array models helpful. An array represents multiplication as a rectangular arrangement of objects. To represent 19 x 3, you would draw a rectangle with 19 rows and 3 columns. Counting all the objects in the rectangle would give you the answer, 57. Similarly, the grid method breaks down the numbers into tens and ones, then performs individual multiplications and additions within a grid format, providing a clear visual representation of the process.
The Mathematical Underpinnings: Place Value and the Distributive Property
The success of all the methods above relies on a firm grasp of two key mathematical concepts:
-
Place Value: This fundamental concept dictates the value of a digit based on its position in a number. In 19, the '1' represents 1 ten (or 10) and the '9' represents 9 ones. Understanding place value is crucial for performing multi-digit multiplication accurately.
-
Distributive Property: As explained earlier, the distributive property allows us to break down a multiplication problem into smaller, more manageable parts. This property is fundamental in algebra and higher-level mathematics. It allows us to expand expressions and simplify complex calculations.
Real-World Applications of 19 x 3
While seemingly a simple problem, 19 x 3 has real-world applications:
- Pricing: Imagine buying 3 items that cost $19 each. The total cost would be 19 x 3 = $57.
- Measurement: If you have 19 rows of plants with 3 plants in each row, you have a total of 57 plants.
- Counting: Any scenario involving counting groups of objects can utilize this multiplication.
Beyond the Basics: Extending the Concept
Understanding 19 x 3 provides a strong foundation for tackling more complex multiplication problems. The same principles – place value, distributive property, and repeated addition – can be applied to larger numbers. This understanding builds the necessary skills for algebra, geometry, and even calculus. Mastering these fundamental mathematical concepts opens doors to a deeper appreciation of mathematics and its vast applications.
Common Misconceptions and Troubleshooting
- Carrying Errors: A common mistake in traditional multiplication is making errors while carrying over digits. Careful attention to detail and double-checking work are essential.
- Misunderstanding Place Value: A lack of understanding of place value can lead to incorrect answers. Regular practice and reinforcement of this concept are crucial.
- Incorrect Application of the Distributive Property: When applying the distributive property, ensure that each term within the parentheses is multiplied by the term outside.
Frequently Asked Questions (FAQ)
-
Q: What is the quickest way to solve 19 x 3?
- A: The quickest method depends on individual preference and skill level. The traditional algorithm is often the fastest for those proficient with it. However, the distributive property can also be quite efficient for mental math.
-
Q: Can I use a calculator to solve 19 x 3?
- A: Yes, a calculator provides a quick and accurate solution. However, understanding the underlying mathematical principles is equally important.
-
Q: How can I help my child understand 19 x 3?
- A: Use visual aids like arrays, counters, or objects to represent the multiplication. Explain the concept through repeated addition and relate it to real-world scenarios. Break down the problem into smaller, manageable steps, and encourage practice.
-
Q: What if I get the wrong answer?
- A: Double-check your work, carefully reviewing each step. If you're still struggling, try a different method or seek assistance from a teacher, tutor, or online resources.
Conclusion: The Significance of Understanding 19 x 3
The seemingly simple problem of 19 x 3 reveals the elegance and power of basic arithmetic. By exploring different methods and understanding the underlying mathematical principles, we gain a deeper appreciation for the interconnectedness of mathematical concepts. This understanding is not merely about finding the answer (57); it's about developing critical thinking skills, problem-solving abilities, and a foundational understanding of mathematics that serves as a springboard for more advanced learning. Mastering this seemingly simple equation unlocks a world of mathematical possibilities. It demonstrates that even the most basic calculations hold immense value in building a strong mathematical foundation. The journey to understanding 19 x 3 is not just about the destination (the answer); it's about the enriching and enlightening process of learning along the way.
Latest Posts
Latest Posts
-
Seven Sizzling Sausages
Sep 16, 2025
-
50 0 2
Sep 16, 2025
-
1 56m In Feet
Sep 16, 2025
-
0 02 To Fraction
Sep 16, 2025
-
Microgram To Gram
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 19 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.