1800 Times 12
interactiveleap
Sep 24, 2025 · 5 min read
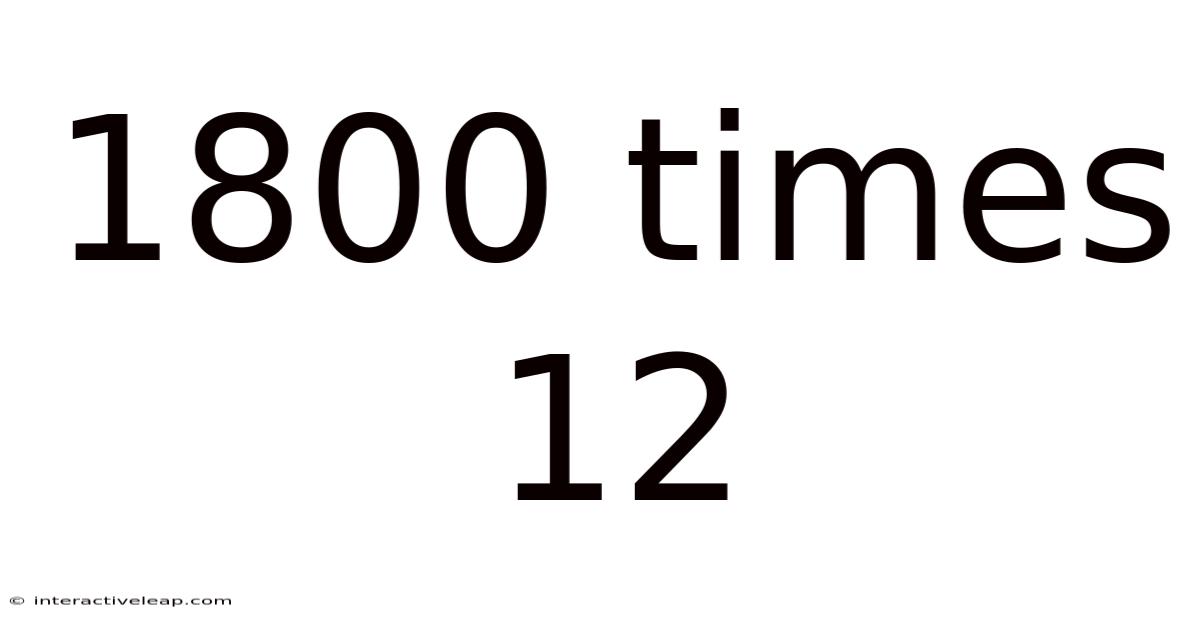
Table of Contents
Unlocking the Power of Multiplication: A Deep Dive into 1800 x 12
This article explores the seemingly simple multiplication problem of 1800 x 12, delving far beyond a simple numerical answer. We’ll unpack various methods of solving this problem, highlighting the underlying mathematical principles and showcasing the practical applications of such calculations in everyday life. This exploration aims to build a strong understanding of multiplication, offering insights valuable for students and adults alike, fostering a deeper appreciation for the beauty and utility of mathematics.
I. Introduction: More Than Just Numbers
The seemingly straightforward calculation of 1800 multiplied by 12 might seem trivial at first glance. However, this problem offers a gateway to understanding fundamental mathematical concepts, including place value, distributive property, and the efficiency of different calculation methods. Understanding how to solve this, and similar problems, is crucial for various applications, from budgeting and finance to engineering and scientific calculations. This exploration will provide multiple approaches, catering to different learning styles and highlighting the interconnectedness of mathematical concepts.
II. Method 1: Standard Multiplication Algorithm
The most common method taught in schools involves the standard multiplication algorithm. Let's break down the steps:
-
Set up the problem: Write the numbers vertically, one above the other, aligning the units digits.
1800 x 12 ---- -
Multiply by the units digit: Multiply 1800 by 2 (the units digit of 12).
1800 x 12 ---- 3600 (1800 x 2 = 3600) -
Multiply by the tens digit: Multiply 1800 by 10 (the tens digit of 12). Notice we're essentially multiplying by 1 and adding a zero as a placeholder.
1800 x 12 ---- 3600
18000 (1800 x 10 = 18000)
4. **Add the partial products:** Add the results from steps 2 and 3.
1800 x 12
3600 18000
21600
Therefore, 1800 x 12 = **21600**.
### III. Method 2: Distributive Property
The distributive property states that a(b + c) = ab + ac. We can use this property to simplify the multiplication:
1. **Break down the multiplier:** Rewrite 12 as 10 + 2.
2. **Apply the distributive property:** 1800 x (10 + 2) = (1800 x 10) + (1800 x 2)
3. **Calculate the partial products:** 1800 x 10 = 18000 and 1800 x 2 = 3600
4. **Add the partial products:** 18000 + 3600 = 21600
Again, we arrive at the answer: 1800 x 12 = **21600**. This method highlights the underlying mathematical principle and can be particularly helpful for mental calculation.
### IV. Method 3: Mental Math Techniques
For those comfortable with mental arithmetic, several techniques can streamline the calculation:
* **Breaking down the numbers:** Think of 1800 as 18 x 100. Then, multiply 18 x 12 = 216. Finally, multiply 216 x 100 = 21600. This approach leverages the associative property of multiplication.
* **Using multiples of 10:** Multiply 1800 x 10 = 18000. Then, multiply 1800 x 2 = 3600. Add the two results: 18000 + 3600 = 21600. This method mirrors the distributive property but simplifies the mental process.
* **Rounding and adjustment:** While less precise for this specific problem, rounding can be useful for estimations. Rounding 12 to 10 would give 18000. Then, account for the difference (1800 x 2 = 3600) and add it to the rounded result.
### V. Real-World Applications
Understanding multiplication, especially with larger numbers like this example, has practical applications across various fields:
* **Finance and Budgeting:** Calculating monthly payments, total costs, or investment returns often involves multiplication of larger numbers.
* **Engineering and Construction:** Calculating material quantities, distances, or areas requires precise multiplication to ensure accuracy and efficiency in projects.
* **Scientific Calculations:** In physics, chemistry, and other sciences, multiplication is fundamental to solving problems and analyzing data.
* **Data Analysis:** Working with datasets often requires performing calculations involving large numbers, including multiplication.
* **Everyday Life:** Even simple tasks like calculating the total cost of groceries or determining the distance traveled can involve multiplication.
### VI. Expanding the Understanding: Place Value and Properties of Multiplication
This problem provides an excellent opportunity to reinforce fundamental mathematical concepts:
* **Place Value:** Understanding place value (ones, tens, hundreds, thousands) is crucial for accurately performing the multiplication algorithm. Each digit's position determines its value.
* **Associative Property:** The associative property states that the grouping of numbers in multiplication doesn't affect the result. (a x b) x c = a x (b x c). This allows us to rearrange the calculation to simplify it.
* **Commutative Property:** The commutative property states that the order of numbers in multiplication doesn't affect the result. a x b = b x a. While not directly used in this specific solution, it's a vital property to understand.
* **Distributive Property:** As demonstrated earlier, this property is invaluable for breaking down complex multiplications into simpler steps.
### VII. Beyond 1800 x 12: Extending the Learning
The techniques and principles discussed here are applicable to a wide range of multiplication problems. By understanding the underlying concepts, you can confidently tackle more challenging calculations. Practice is key to mastering multiplication and developing strong mathematical intuition. Consider exploring similar problems, such as:
* 2500 x 15
* 3600 x 11
* 1250 x 24
### VIII. Frequently Asked Questions (FAQ)
* **Q: What is the quickest way to solve 1800 x 12?**
**A:** The quickest method depends on individual preference and mathematical fluency. Mental math techniques using multiples of 10, as described above, can be very efficient for those comfortable with them. Otherwise, the standard algorithm provides a reliable and systematic approach.
* **Q: Are there any shortcuts for multiplying by 12?**
**A:** While there isn't a single "shortcut" for multiplying by 12, breaking down 12 into (10 + 2) and applying the distributive property simplifies the calculation.
* **Q: Why is understanding the distributive property important?**
**A:** The distributive property is a fundamental concept that simplifies complex multiplications and allows for more efficient problem-solving. It's applicable across various mathematical areas and is essential for advanced mathematical operations.
* **Q: How can I improve my multiplication skills?**
**A:** Consistent practice is crucial. Start with simpler problems and gradually increase the complexity. Focus on understanding the underlying principles and explore different calculation methods to find the ones that suit your learning style best.
### IX. Conclusion: Mastering Multiplication – A Continuous Journey
Solving 1800 x 12 is more than just finding the answer (21600). It's about understanding the underlying mathematical principles, appreciating the power of different calculation methods, and recognizing the broad applicability of multiplication in various aspects of life. By mastering these concepts, you not only improve your mathematical skills but also develop valuable problem-solving abilities applicable far beyond the realm of numbers. Continue practicing, exploring different approaches, and deepening your understanding of mathematical concepts – the journey of mathematical mastery is a continuous and rewarding one.
Latest Posts
Latest Posts
-
Those Seen Dancing
Sep 24, 2025
-
2n 2 Sequence
Sep 24, 2025
-
85 Of 15
Sep 24, 2025
-
Dog Bows Christmas
Sep 24, 2025
-
100l In Gallons
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1800 Times 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.