16 X Pi
interactiveleap
Sep 13, 2025 · 5 min read
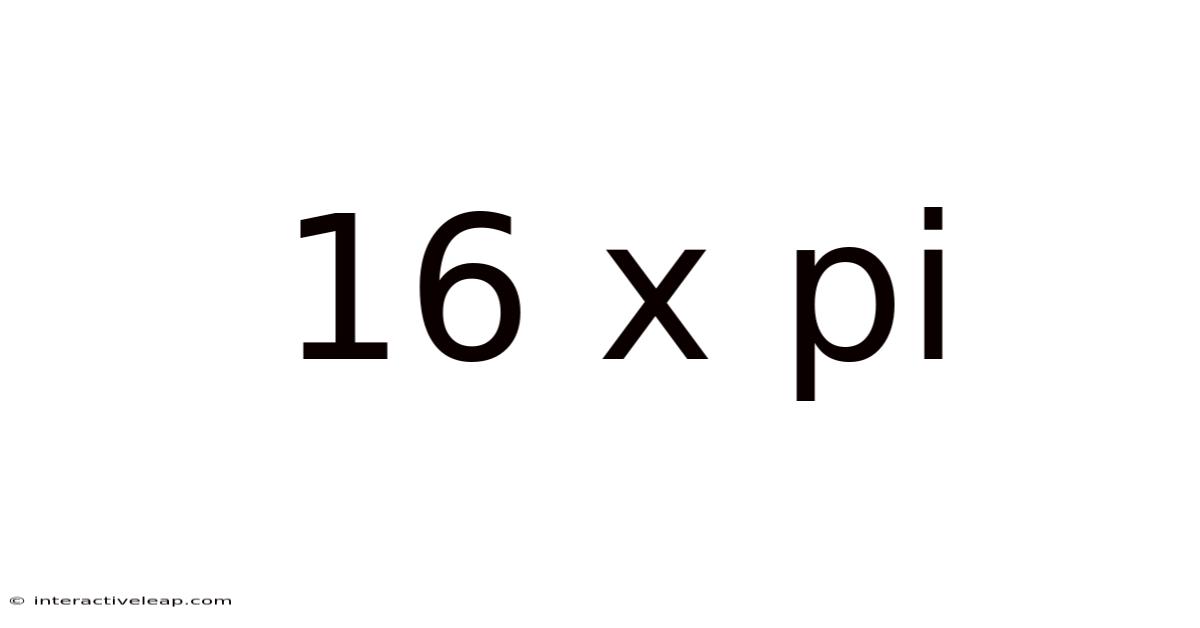
Table of Contents
Unraveling the Mystery of 16π: Exploring the Mathematical Constant
The number π (pi), approximately 3.14159, is a fundamental constant in mathematics, representing the ratio of a circle's circumference to its diameter. It's a number that has captivated mathematicians and scientists for centuries, appearing in countless formulas across various fields. This article delves into the seemingly simple yet surprisingly rich mathematical concept of 16π, exploring its significance, applications, and the intriguing connections it holds within the broader mathematical landscape. We'll journey from its basic definition to its more advanced implications, suitable for anyone with a basic understanding of mathematics.
Understanding the Basics: What is 16π?
At its core, 16π is simply the product of 16 and π. This means it's approximately 16 * 3.14159 = 50.26544. While seemingly straightforward, the significance of 16π stems from its frequent appearance in various geometric and mathematical contexts. Unlike π itself, which is an irrational number (meaning its decimal representation never terminates or repeats), 16π remains irrational. However, its approximate value allows for practical applications in numerous real-world scenarios.
Geometric Applications: Where 16π Shows Up
The number 16π frequently arises in calculations involving circles and spheres. Let's explore some key examples:
1. Circumference of a Circle with Radius 8: The formula for the circumference of a circle is C = 2πr, where 'r' is the radius. If the radius is 8 units, the circumference is C = 2π(8) = 16π. This simple example highlights how 16π directly represents the circumference of a specific circle.
2. Surface Area of a Sphere with Radius 4: The surface area of a sphere is given by A = 4πr², where 'r' is the radius. With a radius of 4 units, the surface area becomes A = 4π(4)² = 64π. While not directly 16π, this calculation demonstrates the prevalence of π-related values in spherical geometry. Note that half of this surface area, 32π, is still closely related to our target number, exhibiting the interconnectedness of these concepts.
3. Volume of a Cylinder: Consider a cylinder with radius 4 and height 1. The volume is given by V = πr²h. With our given values, the volume is π(4)²(1) = 16π. This exemplifies the appearance of 16π in volume calculations, further showcasing its importance in three-dimensional geometry.
4. Beyond Simple Shapes: While these examples focus on simple shapes, the application of 16π extends to more complex geometric problems. For instance, calculating the arc length of a specific sector of a circle with a particular radius and central angle will often involve multiples of π, potentially including 16π in certain configurations.
Mathematical Significance: 16π in Advanced Concepts
The significance of 16π extends beyond simple geometric calculations. It pops up in:
-
Fourier Series: These mathematical series are used to represent periodic functions as a sum of sine and cosine waves. The coefficients in these series can often involve multiples of π, including 16π, depending on the specific function being represented.
-
Integral Calculus: In integral calculus, evaluating definite integrals involving trigonometric functions often results in expressions containing multiples of π. Certain definite integrals may specifically yield 16π as a result.
-
Complex Analysis: The number 16π, like other multiples of π, appears frequently in complex analysis calculations, particularly those involving contour integrals and residue theorems. These are advanced concepts within mathematics and illustrate 16π's profound relevance in more abstract mathematical contexts.
Practical Applications: Real-World Uses of 16π
While the mathematical underpinnings are fascinating, the practical applications of 16π (and other multiples of π) are crucial in diverse fields:
-
Engineering: Civil engineers use calculations involving π to design structures such as bridges, tunnels, and buildings. Calculations related to circular components or curved surfaces often necessitate utilizing multiples of π, such as 16π.
-
Physics: In physics, π appears in formulas related to oscillations, waves, and electromagnetism. Calculations involving circular motion or wave phenomena often involve multiples of π in their solutions.
-
Computer Graphics: Generating realistic images and simulations relies on precise mathematical calculations. Representing circular objects or simulating physical phenomena often requires using π and its multiples, including 16π.
Exploring Related Concepts: Beyond 16π
Understanding 16π allows a deeper appreciation of related mathematical concepts:
-
Multiples of π: The appearance of 16π highlights the broader significance of multiples of π (2π, 4π, 8π, etc.) in mathematics and its applications. Each multiple represents a specific geometric or mathematical context.
-
Irrational Numbers: The fact that 16π is an irrational number reinforces the importance of understanding and working with irrational numbers in mathematical calculations. Approximations are often necessary but understanding the inherent nature of the number remains crucial.
-
Approximation Techniques: Since π is an irrational number, approximations are essential for practical calculations. Understanding how to approximate 16π effectively is a valuable skill in various fields.
Frequently Asked Questions (FAQ)
Q: Is 16π a rational or irrational number?
A: 16π is an irrational number. Since π is irrational (its decimal representation never ends or repeats), multiplying it by 16 doesn't change its irrational nature.
Q: What is the approximate value of 16π?
A: The approximate value of 16π is 50.2654824574... This is obtained by multiplying 16 by the approximate value of π (3.1415926535...).
Q: Are there any other significant multiples of π besides 16π?
A: Yes, many multiples of π are significant, including 2π (related to the circumference of a unit circle), 4π (related to the surface area of a unit sphere), and others that appear frequently in various mathematical formulas and applications.
Q: How is 16π used in computer programming?
A: In computer programming, 16π might be used in simulations, game development (creating circular objects or calculating projectile trajectories), or any application requiring precise geometric calculations, often using a sufficiently accurate approximation of π.
Conclusion: The Enduring Relevance of 16π
16π, while appearing as a simple mathematical expression, showcases the profound and far-reaching impact of the mathematical constant π. From elementary geometry to advanced calculus and practical applications in engineering and physics, 16π, and other multiples of π, illustrate the interconnectedness and enduring relevance of this fundamental number in the mathematical world. Understanding 16π is not merely about knowing its numerical value; it’s about appreciating its role within a broader tapestry of mathematical concepts and real-world applications. Its seemingly simple form belies a complex and fascinating history, continuing to inspire and challenge mathematicians and scientists alike. Further exploration into the world of π and its multiples unveils a rich landscape of mathematical beauty and practical utility.
Latest Posts
Latest Posts
-
Manual Impact Driver
Sep 14, 2025
-
75 Of 45
Sep 14, 2025
-
Sugar Rush Vanellope
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 16 X Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.