15 Of 9
interactiveleap
Sep 24, 2025 · 5 min read
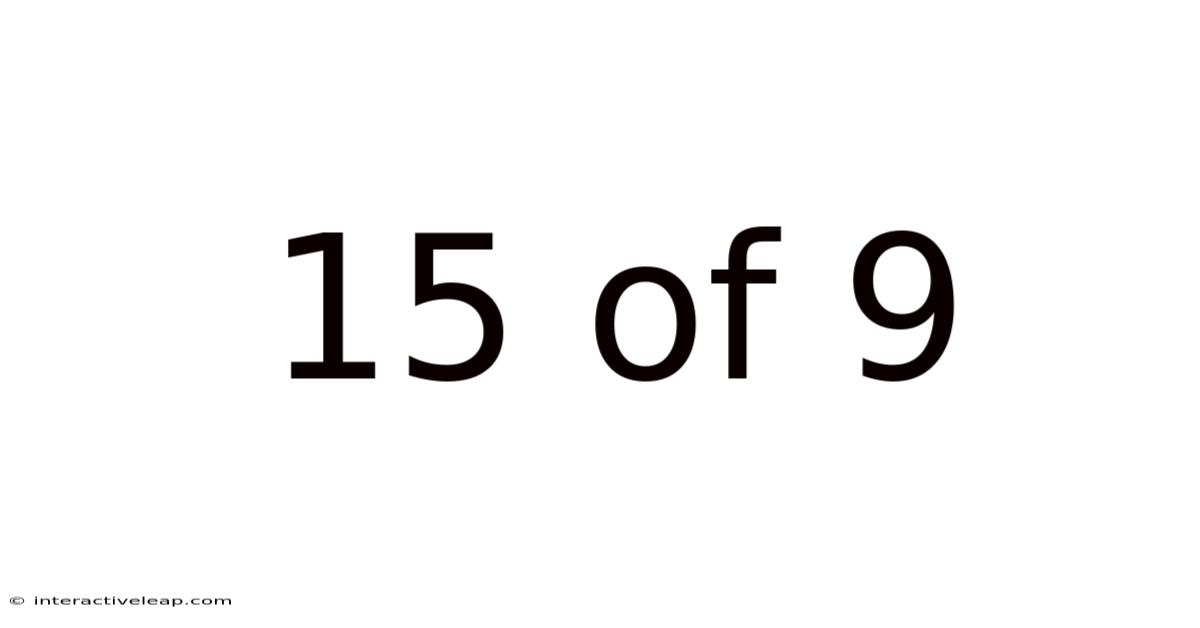
Table of Contents
Decoding the Enigma: Understanding the Fraction 15/9
The seemingly simple fraction 15/9 often presents a challenge, especially for those new to fractions or struggling with their simplification. This article delves deep into understanding 15/9, exploring its different representations, its practical applications, and addressing common misconceptions. We’ll cover everything from basic simplification to its decimal equivalent and even touch upon its use in real-world scenarios. By the end, you'll not only understand 15/9 but also gain a more robust understanding of fractions in general.
Introduction: What is 15/9?
15/9 represents a fraction, a part of a whole. The number 15 is the numerator, indicating the number of parts we have. The number 9 is the denominator, indicating the total number of equal parts the whole is divided into. Essentially, 15/9 means we have 15 out of 9 equal parts. This immediately suggests that we have more than one whole. Understanding this basic concept is crucial to comprehending the fraction's true meaning.
Simplifying 15/9: Finding the Lowest Terms
One of the fundamental principles of working with fractions is to simplify them to their lowest terms. This makes the fraction easier to understand and work with in calculations. To simplify 15/9, we find the greatest common divisor (GCD) of both the numerator and the denominator. The GCD is the largest number that divides both 15 and 9 without leaving a remainder.
In this case, the GCD of 15 and 9 is 3. We divide both the numerator and the denominator by 3:
15 ÷ 3 = 5 9 ÷ 3 = 3
Therefore, the simplified form of 15/9 is 5/3. This means we have five parts out of a total of three equal parts. Again, this clearly indicates that we have more than one whole.
Representing 15/9: Mixed Numbers and Improper Fractions
Fractions like 5/3, where the numerator is larger than the denominator, are called improper fractions. They represent a value greater than one. Improper fractions can be converted into mixed numbers, which combine a whole number and a proper fraction (where the numerator is smaller than the denominator).
To convert 5/3 into a mixed number, we perform division:
5 ÷ 3 = 1 with a remainder of 2
This means 5/3 can be expressed as 1 2/3. This represents one whole and two-thirds of another. Both 5/3 and 1 2/3 are equivalent representations of 15/9. Understanding these different representations is essential for solving various mathematical problems.
Decimal Equivalent of 15/9
Converting a fraction to its decimal equivalent involves dividing the numerator by the denominator. For 15/9 (or its simplified form, 5/3):
5 ÷ 3 ≈ 1.666666...
The result is a repeating decimal, indicated by the ellipsis (...). The digit 6 repeats infinitely. This repeating decimal can be represented as 1.6̅6̅. The bar above the 6 indicates that it repeats indefinitely. This decimal representation is another way to understand the value of the fraction 15/9.
Practical Applications of 15/9
Fractions like 15/9 are frequently encountered in various real-world applications. Consider these examples:
- Cooking and Baking: Recipes often require fractional measurements. If a recipe calls for 15/9 cups of flour, you would simplify it to 5/3 cups and then convert it to a mixed number (1 2/3 cups) for easier measurement.
- Construction and Engineering: Calculations in construction and engineering often involve fractions. For example, determining the length of a beam or the amount of material needed might involve fractions that need simplification and conversion.
- Data Analysis: In data analysis, fractions can represent proportions or percentages. For example, if 15 out of 9 students passed an exam, this represents 15/9, simplifying to 5/3 which is approximately 166.67%.
- Finance: Fractions are used extensively in financial calculations, such as calculating interest rates, profit margins, or stock prices.
Common Misconceptions about 15/9
- Confusing Simplification with Solving: Some students mistake simplifying a fraction for solving a problem. Simplifying 15/9 to 5/3 doesn't change the value; it just changes its representation.
- Ignoring the Remainder: When converting an improper fraction to a mixed number, the remainder is crucial and must be included as part of the fraction.
- Decimal Rounding Errors: When converting to decimals, it's crucial to understand that 1.666… is not exactly equal to 1.67. Rounding off can introduce inaccuracies in calculations.
Further Exploration: Working with 15/9 in Equations
Understanding 15/9 allows for easier manipulation in mathematical equations. For example:
- Addition: Adding 15/9 to another fraction would involve simplifying 15/9 first to 5/3, and then finding a common denominator before adding.
- Subtraction: Similar to addition, simplification and finding a common denominator are essential before subtracting 15/9 from another fraction.
- Multiplication: Multiplying 15/9 by another fraction would also benefit from simplifying 15/9 to 5/3 first to make the calculation simpler.
- Division: Dividing by 15/9 is the same as multiplying by its reciprocal (3/5). Simplifying 15/9 simplifies this process.
Frequently Asked Questions (FAQs)
Q: Is 15/9 the same as 5/3?
A: Yes, 15/9 simplifies to 5/3. Both represent the same value.
Q: How do I convert 15/9 to a percentage?
A: First, simplify 15/9 to 5/3. Then divide 5 by 3 to get approximately 1.6667. Multiply by 100 to get approximately 166.67%.
Q: Can I add 15/9 directly to another fraction without simplifying?
A: While you can, it’s much easier and less prone to errors to simplify 15/9 to 5/3 first before adding it to another fraction.
Q: What is the reciprocal of 15/9?
A: The reciprocal of 15/9 (or 5/3) is 3/5.
Conclusion: Mastering the Fraction 15/9 and Beyond
Understanding the fraction 15/9 goes beyond simply knowing its value. It involves a deeper comprehension of fraction simplification, equivalent representations (improper fractions, mixed numbers, and decimals), and its application in real-world scenarios. Mastering this seemingly simple fraction provides a strong foundation for tackling more complex fractional calculations and solidifies your understanding of fundamental mathematical concepts. By grasping the principles outlined in this article, you'll not only understand 15/9 but also gain a more confident approach to working with fractions in various contexts. Remember, practice is key to mastering fractions. The more you work with them, the more comfortable and proficient you’ll become.
Latest Posts
Latest Posts
-
3 M Square
Sep 24, 2025
-
Wednesdays Child Poem
Sep 24, 2025
-
4 75 Of 20000
Sep 24, 2025
-
155lbs In Kg
Sep 24, 2025
-
0 08 To Percentage
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 15 Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.