0.08 To Percentage
interactiveleap
Sep 24, 2025 · 5 min read
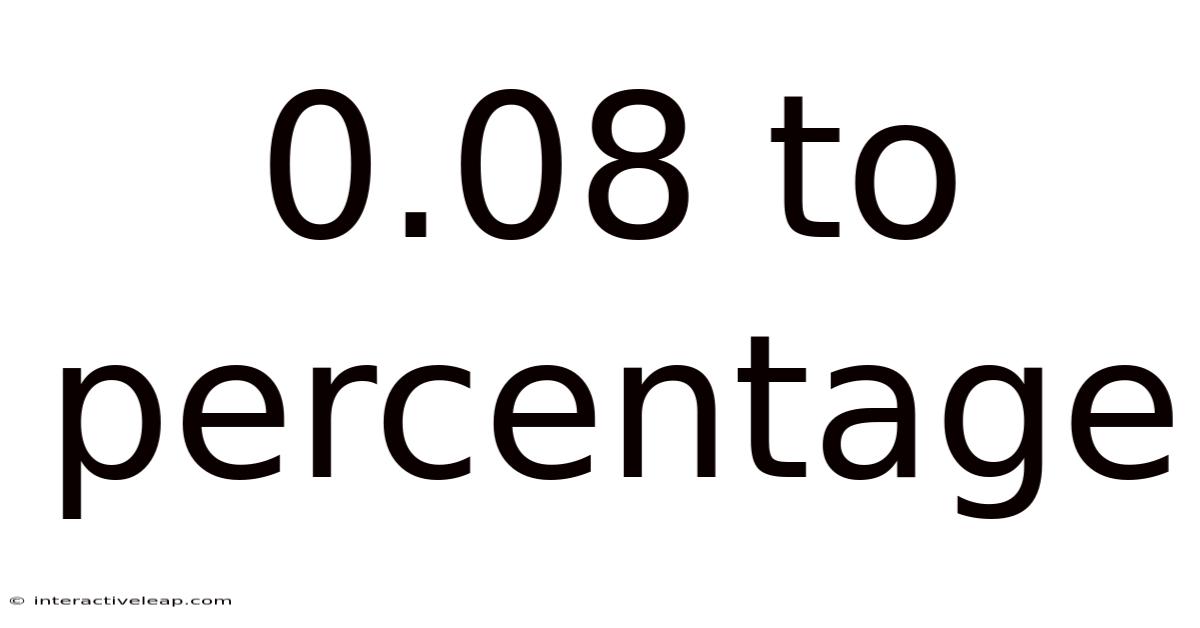
Table of Contents
Converting 0.08 to a Percentage: A Comprehensive Guide
Understanding how to convert decimals to percentages is a fundamental skill in mathematics and a crucial part of many everyday applications, from calculating discounts and interest rates to interpreting data in various fields. This article will comprehensively guide you through the process of converting 0.08 to a percentage, explaining the underlying principles and offering practical examples to solidify your understanding. We'll also delve into related concepts and address frequently asked questions to ensure a complete grasp of this essential mathematical concept.
Introduction: Decimals, Fractions, and Percentages – A Unified Perspective
Before we dive into the conversion, let's briefly review the relationships between decimals, fractions, and percentages. They are all different ways of representing parts of a whole. A fraction expresses a part of a whole using a numerator (top number) and a denominator (bottom number), like 1/2. A decimal represents a part of a whole using a base-ten system, like 0.5. A percentage represents a part of a whole as a fraction of 100, denoted by the "%" symbol, like 50%. These three representations are interconnected and can be easily converted from one form to another.
Converting 0.08 to a Percentage: The Simple Method
The most straightforward method for converting a decimal to a percentage is to multiply the decimal by 100%. This is because a percentage is simply a fraction with a denominator of 100.
Let's apply this to 0.08:
0.08 * 100% = 8%
Therefore, 0.08 is equivalent to 8%. This simple multiplication effectively shifts the decimal point two places to the right, adding the percentage symbol to complete the conversion.
Understanding the Underlying Principle
The reason multiplying by 100% works is rooted in the definition of percentage. "Percent" literally means "per hundred" (from the Latin per centum). Therefore, a percentage represents the number of parts out of 100. Multiplying a decimal by 100 essentially expresses the decimal as a fraction with a denominator of 100, which is the definition of a percentage.
For instance, 0.08 can be expressed as the fraction 8/100. This fraction directly translates to 8%, as it represents 8 parts out of 100.
Practical Applications: Real-World Examples
The ability to convert decimals to percentages is crucial in many real-world scenarios. Consider the following examples:
-
Calculating Discounts: A store offers a 0.08 discount on all items. This is equivalent to an 8% discount. If an item costs $50, the discount would be $50 * 0.08 = $4, resulting in a final price of $46.
-
Determining Interest Rates: An investment account offers an annual interest rate of 0.08. This equates to an 8% annual interest rate. If you invest $1000, you would earn $1000 * 0.08 = $80 in interest after one year.
-
Analyzing Statistical Data: In statistical analysis, data is often presented as decimals. Converting these decimals to percentages makes the data easier to understand and interpret. For instance, if a survey shows that 0.08 of respondents prefer a particular product, this can be expressed as 8% preference.
-
Grading Systems: In some grading systems, scores are presented as decimals. Converting these decimals to percentages allows for a more readily understandable representation of the student's performance. For example, a score of 0.08 on a test might be equivalent to 8%, depending on the grading scale used.
Beyond the Basics: Working with Larger and Smaller Decimals
The method of multiplying by 100% applies equally to decimals larger and smaller than 0.08. For example:
- Converting 0.5 to a percentage: 0.5 * 100% = 50%
- Converting 1.25 to a percentage: 1.25 * 100% = 125% (Note that percentages can exceed 100%)
- Converting 0.005 to a percentage: 0.005 * 100% = 0.5%
Dealing with Fractions Before Conversion
If you encounter a fraction instead of a decimal, you must first convert the fraction to a decimal before applying the percentage conversion method. This involves dividing the numerator by the denominator. For example:
To convert 1/4 to a percentage:
- Convert 1/4 to a decimal: 1 ÷ 4 = 0.25
- Convert the decimal to a percentage: 0.25 * 100% = 25%
Advanced Concepts: Understanding Percentage Change
While the conversion of 0.08 to a percentage is straightforward, understanding percentage change requires additional steps. Percentage change calculates the relative difference between two values. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100%
For example, if a value increases from 100 to 108, the percentage increase is:
[(108 - 100) / 100] * 100% = 8%
This signifies an 8% increase from the original value.
Frequently Asked Questions (FAQ)
-
Q: Can percentages be greater than 100%? A: Yes, percentages can exceed 100%. This indicates that the value being represented is greater than the whole. For example, if a company's sales increased by 150%, it means its sales have more than doubled.
-
Q: How do I convert a percentage back to a decimal? A: To convert a percentage back to a decimal, divide the percentage by 100. For example, 8% becomes 8/100 = 0.08.
-
Q: What if the decimal has more than two decimal places? A: The process remains the same. Simply multiply the decimal by 100% to obtain the percentage equivalent. For instance, 0.0875 * 100% = 8.75%
-
Q: Why is understanding percentage conversions important? A: Percentage conversions are fundamental to various aspects of life, including finance, statistics, data analysis, and everyday calculations involving discounts, interest rates, and proportions.
-
Q: Are there online calculators for decimal-to-percentage conversions? A: While this article provides the method for manual calculation, many online calculators are available to perform these conversions quickly and easily, although it’s always beneficial to understand the underlying principles involved.
Conclusion: Mastering the Art of Percentage Conversions
Converting decimals to percentages, and vice-versa, is a valuable skill with numerous practical applications. By understanding the underlying principles and applying the simple method of multiplying by 100%, you can confidently navigate various situations requiring these conversions. Remember that this skill is not just about manipulating numbers; it’s about interpreting and understanding data more effectively in various contexts. This article has provided a thorough guide, equipping you with the knowledge and confidence to handle decimal-to-percentage conversions with ease. With practice and consistent application, you’ll quickly master this fundamental mathematical concept.
Latest Posts
Latest Posts
-
70s Punk Style
Sep 24, 2025
-
48 Times 3
Sep 24, 2025
-
40kmph To Mph
Sep 24, 2025
-
26stone In Kg
Sep 24, 2025
-
Oasis Water Purification
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 0.08 To Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.