12 Of 650
interactiveleap
Sep 20, 2025 · 5 min read
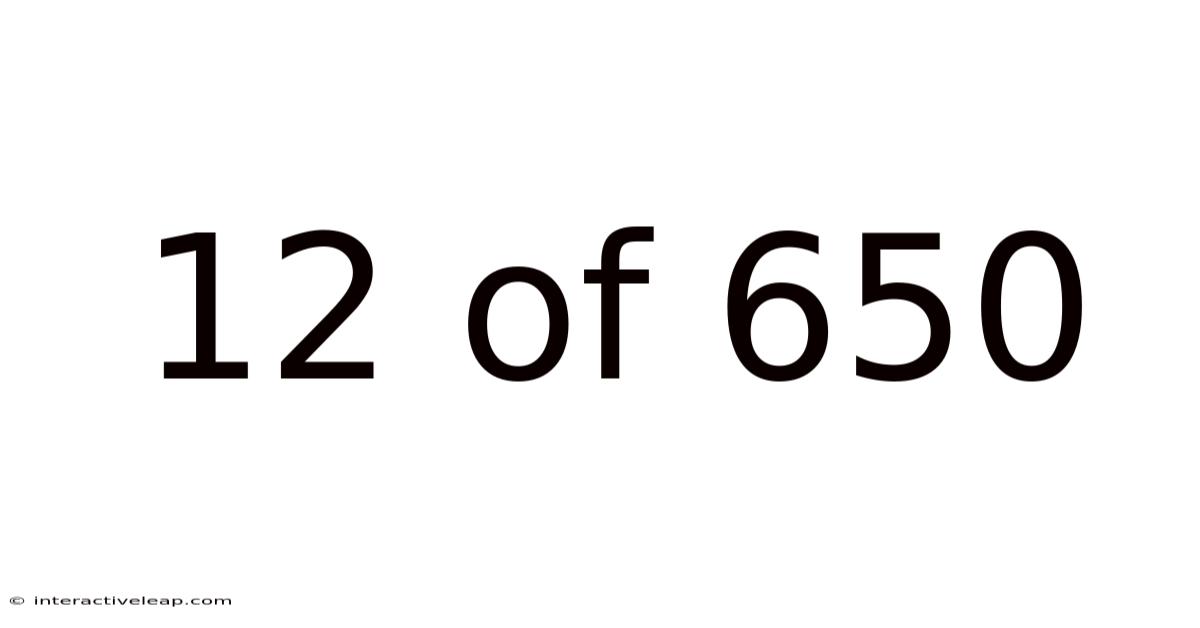
Table of Contents
Decoding the Mystery: Understanding the Fraction 12/650
The seemingly simple fraction 12/650 often presents a challenge, particularly when dealing with concepts like simplification, percentage conversion, and real-world applications. This comprehensive guide will unravel the complexities surrounding 12/650, providing a step-by-step approach to understanding its value and significance. We'll explore its simplification, decimal and percentage equivalents, and delve into practical scenarios where this fraction might arise. By the end, you'll confidently handle fractions similar to 12/650, solidifying your foundational understanding of fractional mathematics.
I. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
The first step in working with any fraction is simplification. This process involves reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator (12) and the denominator (650). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
To find the GCD of 12 and 650, we can use the Euclidean algorithm or prime factorization. Let's utilize prime factorization:
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 650: 2 x 5 x 5 x 13 = 2 x 5² x 13
By comparing the prime factorizations, we identify the common factor as 2. Therefore, the GCD of 12 and 650 is 2.
Now, we divide both the numerator and the denominator by the GCD (2):
12 ÷ 2 = 6 650 ÷ 2 = 325
Therefore, the simplified form of 12/650 is 6/325. This simplified fraction is much easier to work with in calculations and provides a clearer understanding of the fraction's value.
II. Converting the Fraction to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. Using the simplified fraction 6/325:
6 ÷ 325 ≈ 0.01846
Therefore, the decimal equivalent of 12/650 (or 6/325) is approximately 0.01846. The approximation symbol (~) is used because the decimal representation is non-terminating; it continues infinitely. Depending on the context, you might round this decimal to a specific number of decimal places (e.g., 0.018 or 0.0185).
III. Converting the Fraction to a Percentage
To convert a fraction to a percentage, we multiply the decimal equivalent by 100%. Using the decimal approximation from the previous section (0.01846):
0.01846 x 100% ≈ 1.846%
Therefore, 12/650 is approximately 1.846%. Again, rounding might be necessary based on the level of precision required. This percentage representation provides a readily understandable proportion, especially in contexts involving comparisons or ratios.
IV. Real-World Applications of 12/650
While 12/650 might seem like an abstract mathematical concept, it can represent numerous real-world scenarios. Consider these examples:
-
Proportions: Imagine a survey where 12 out of 650 respondents answered "yes" to a particular question. The fraction 12/650, simplified to 6/325 or expressed as a percentage (approximately 1.85%), provides a concise summary of the response distribution.
-
Ratios: If a mixture contains 12 grams of substance A and 650 grams of substance B, the fraction 12/650 represents the ratio of substance A to the total mixture.
-
Probability: In a situation with 650 equally likely outcomes, where 12 outcomes represent a specific event, the fraction 12/650 represents the probability of that event occurring.
-
Discounts: A store might offer a discount of 12/650 (or approximately 1.85%) on selected items.
-
Test Scores: A student might answer 12 questions correctly out of a total of 650 questions on an exam. The fraction 12/650 indicates their performance.
V. Expanding on Fraction Concepts: Beyond 12/650
Understanding 12/650 provides a solid foundation for grasping broader concepts in fractional arithmetic. Let's explore some related ideas:
-
Equivalent Fractions: Any fraction that can be simplified to 6/325 is equivalent to 12/650. For example, 18/975, 24/1300, and 30/1625 are all equivalent fractions.
-
Improper Fractions and Mixed Numbers: If the numerator were larger than the denominator, we would have an improper fraction. Converting improper fractions to mixed numbers (a whole number and a proper fraction) is another essential skill in fraction manipulation.
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. Finding the least common multiple (LCM) is crucial in these operations.
-
Multiplying and Dividing Fractions: Multiplying fractions involves multiplying the numerators and denominators separately. Dividing fractions is done by inverting the second fraction and then multiplying.
VI. Frequently Asked Questions (FAQ)
Q: What is the simplest form of 12/650?
A: The simplest form of 12/650 is 6/325.
Q: What is the decimal equivalent of 12/650?
A: The decimal equivalent is approximately 0.01846.
Q: What is the percentage equivalent of 12/650?
A: The percentage equivalent is approximately 1.846%.
Q: Can 12/650 be further simplified beyond 6/325?
A: No, 6 and 325 do not share any common factors other than 1, making 6/325 the simplest form.
Q: How do I convert a fraction to a decimal and a percentage?
A: To convert a fraction to a decimal, divide the numerator by the denominator. To convert a decimal to a percentage, multiply by 100%.
VII. Conclusion: Mastering Fractional Arithmetic
This in-depth exploration of 12/650 showcases the importance of understanding fundamental fractional concepts. From simplification and decimal conversion to real-world applications, we've covered the key aspects of working with this fraction. Remember, mastering these skills is essential for success in various fields, from basic mathematics to advanced scientific and engineering applications. The seemingly simple fraction 12/650 serves as a microcosm of the broader world of fractional arithmetic, highlighting the value of precision, simplification, and practical application. By understanding its nuances, you've taken a significant step towards confidently tackling more complex fractional problems in the future.
Latest Posts
Latest Posts
-
Non Layered Hairstyles
Sep 20, 2025
-
Price Offer Curve
Sep 20, 2025
-
113kg In Pounds
Sep 20, 2025
-
80 Of 280
Sep 20, 2025
-
75 Of 300
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 12 Of 650 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.