12 Of 450
interactiveleap
Sep 21, 2025 · 6 min read
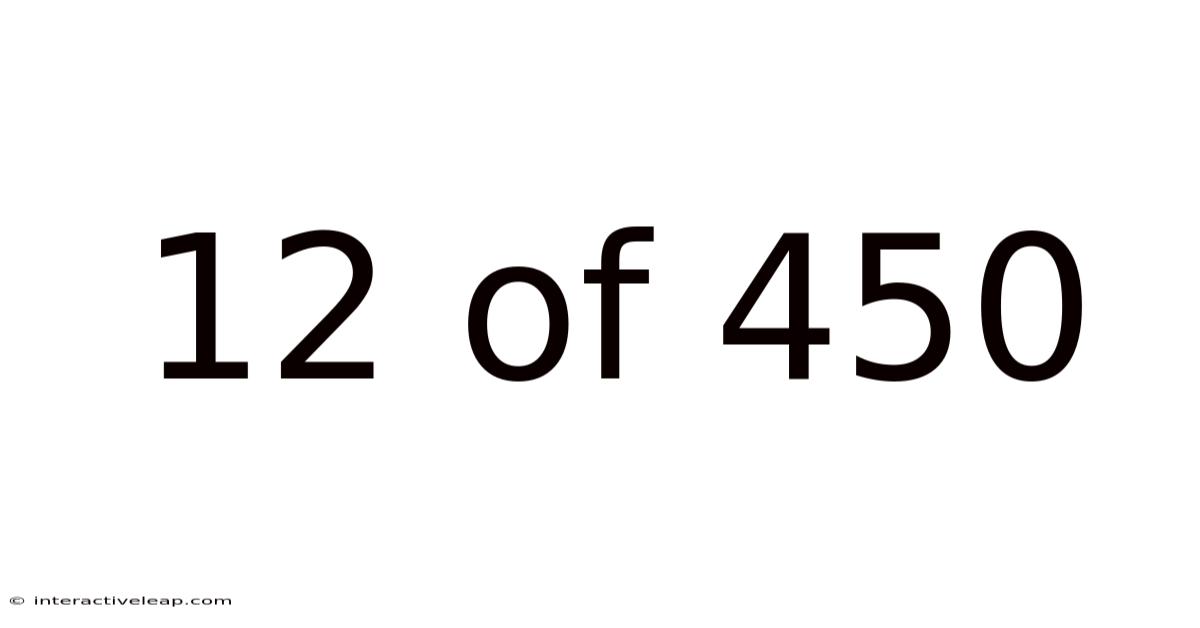
Table of Contents
Decoding the Enigma: Understanding the Fraction 12/450 and its Implications
The seemingly simple fraction 12/450 might appear insignificant at first glance. However, understanding its meaning and implications unveils a broader understanding of fractions, ratios, percentages, and their applications in various fields. This article will delve deep into the fraction 12/450, exploring its simplification, decimal representation, percentage equivalent, and practical applications, all while maintaining a friendly and informative tone suitable for readers of diverse backgrounds. We will also touch upon the mathematical concepts behind simplifying fractions and converting them into different formats.
Introduction: What is 12/450?
12/450 represents a part-to-whole relationship. It signifies 12 units out of a total of 450 units. This fractional representation is crucial in numerous contexts, from calculating proportions in recipes to understanding statistical data and analyzing financial performance. The key to unlocking its full meaning lies in simplifying the fraction and converting it to other forms like decimals and percentages.
Simplifying 12/450: Finding the Greatest Common Divisor (GCD)
Before we delve into other representations, simplifying the fraction is fundamental. This involves finding the greatest common divisor (GCD) of both the numerator (12) and the denominator (450). The GCD is the largest number that divides both numbers without leaving a remainder.
One method to find the GCD is through prime factorization. Let's break down 12 and 450 into their prime factors:
- 12 = 2 x 2 x 3 (2² x 3)
- 450 = 2 x 3 x 3 x 5 x 5 (2 x 3² x 5²)
The common prime factors are 2 and 3. The lowest power of 2 is 2¹ and the lowest power of 3 is 3¹. Therefore, the GCD is 2 x 3 = 6.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
12/6 = 2 450/6 = 75
Therefore, the simplified fraction is 2/75. This simplified form is much easier to work with and provides a clearer representation of the ratio.
Converting 2/75 to a Decimal: Understanding Decimal Representation
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case:
2 ÷ 75 ≈ 0.026666...
The result is a recurring decimal, with the digit 6 repeating infinitely. For practical purposes, we can round this to a specific number of decimal places. Rounding to three decimal places, we get 0.027. Understanding decimal representation allows for easier comparison with other numerical values and simplifies calculations involving decimal systems.
Expressing 2/75 as a Percentage: Interpreting the Proportion
A percentage is a fraction expressed as a part of 100. To convert the fraction 2/75 to a percentage, we can first convert it to a decimal (as shown above) and then multiply by 100:
0.027 x 100 = 2.7%
This means that 12 out of 450 represents 2.7% of the total. Percentage representation is particularly useful for conveying proportions in a readily understandable manner, especially in contexts like statistics, finance, and everyday life.
Practical Applications of 12/450 and its Equivalents: Real-World Scenarios
The fraction 12/450, and its simplified and converted forms, finds applications in various fields:
-
Statistics: Imagine a survey of 450 people, where 12 responded positively to a particular question. The fraction 2/75 or the percentage 2.7% represents the proportion of positive responses within the sample.
-
Inventory Management: If a warehouse has 450 items, and 12 are defective, the fraction represents the proportion of defective items. This information is crucial for quality control and inventory management strategies.
-
Financial Analysis: In financial reports, this fraction could represent a small portion of a larger investment portfolio or a minor percentage of total sales.
-
Recipe Scaling: If a recipe calls for 12 grams of an ingredient in a total mixture of 450 grams, understanding the fraction helps in scaling the recipe up or down proportionally.
-
Probability: In probability calculations, the fraction could represent the probability of a specific event occurring out of a set of possible outcomes.
Further Exploration of Fraction Concepts: Beyond 12/450
Understanding 12/450 provides a stepping stone to understanding more complex fractional concepts:
-
Improper Fractions and Mixed Numbers: Fractions where the numerator is larger than the denominator are called improper fractions. These can be converted to mixed numbers, which consist of a whole number and a proper fraction (e.g., 5 1/2).
-
Equivalent Fractions: Different fractions can represent the same proportion. For example, 12/450, 2/75, and 4/150 are all equivalent fractions.
-
Fraction Operations: Fractions can be added, subtracted, multiplied, and divided, following specific rules. Mastering these operations is crucial for more advanced mathematical concepts.
-
Ratios and Proportions: Fractions are intrinsically linked to ratios and proportions. A ratio is a comparison of two quantities, while a proportion states that two ratios are equal.
-
Complex Fractions: These fractions have fractions within the numerator or denominator or both. Simplifying complex fractions often involves inverting and multiplying.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying a fraction important?
A1: Simplifying fractions makes them easier to understand and work with. It provides a more concise and efficient representation of the proportion. It also simplifies subsequent calculations.
Q2: What are some other methods to find the GCD?
A2: Besides prime factorization, the Euclidean algorithm is another effective method to find the GCD of two numbers.
Q3: How accurate should the decimal representation be?
A3: The required accuracy of the decimal representation depends on the context. In some cases, rounding to a few decimal places is sufficient, while in others, more precision might be needed.
Q4: What are some common errors made when working with fractions?
A4: Common errors include incorrectly simplifying fractions, making mistakes during addition or subtraction (requiring common denominators), and forgetting to consider the order of operations when dealing with multiple operations.
Q5: Are there online tools to simplify fractions?
A5: Yes, many online calculators and websites are available that can simplify fractions, convert them to decimals and percentages, and perform other fraction-related calculations.
Conclusion: Mastering the Fundamentals of Fractions
The seemingly simple fraction 12/450 opens a window into a world of mathematical concepts, practical applications, and problem-solving strategies. By understanding how to simplify fractions, convert them to decimals and percentages, and interpret their meaning within different contexts, we gain a valuable skill applicable across various disciplines. This knowledge forms a solid foundation for further exploration of more complex mathematical topics, equipping us to analyze data, solve problems, and understand the world around us more effectively. The journey from 12/450 to its simplified form, its decimal and percentage equivalents, and its real-world applications demonstrates the power of fundamental mathematical concepts in everyday life. Mastering these fundamentals empowers individuals to approach complex challenges with confidence and clarity.
Latest Posts
Latest Posts
-
Doff Ppe Order
Sep 21, 2025
-
64kgs In Stone
Sep 21, 2025
-
27 X Pi
Sep 21, 2025
-
2500mm In Inches
Sep 21, 2025
-
80 7kg Into Stone
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 12 Of 450 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.