10000 X 100
interactiveleap
Sep 16, 2025 · 6 min read
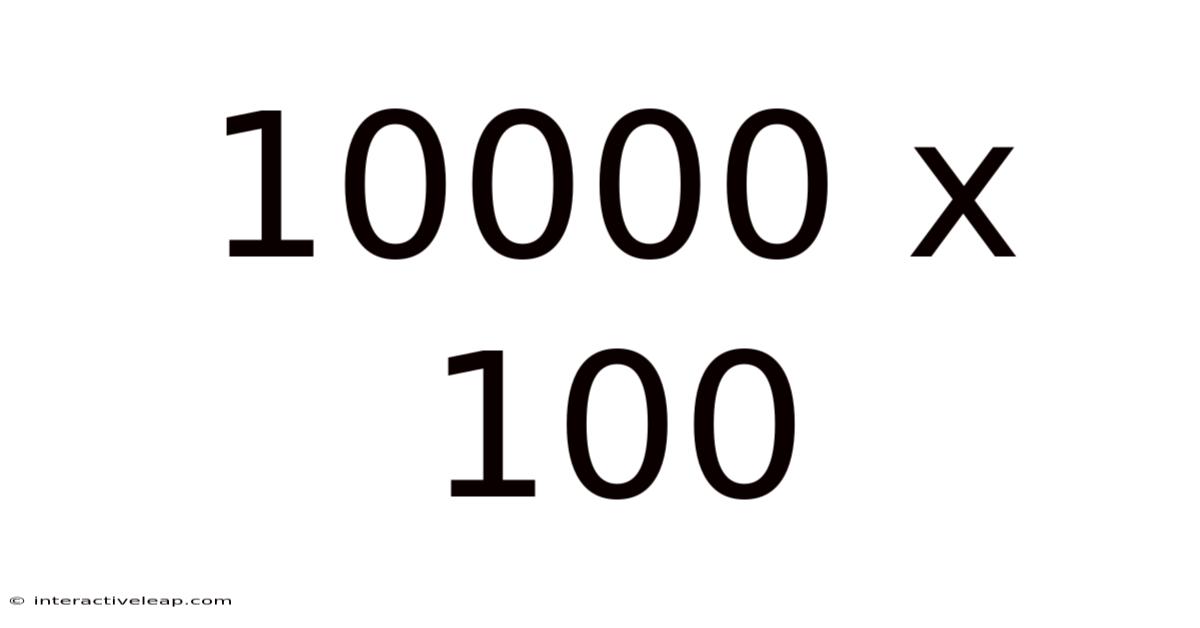
Table of Contents
Decoding 10,000 x 100: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem of 10,000 x 100, delving far beyond the immediate answer to uncover the underlying mathematical principles and its widespread applications in various fields. We'll examine different methods of solving this problem, discuss the significance of place value, explore the concept of scaling and its relevance to real-world scenarios, and finally delve into some fascinating related mathematical concepts. Understanding this seemingly basic calculation unlocks a deeper understanding of numerical manipulation, crucial for success in numerous academic and professional pursuits.
I. The Fundamentals: Solving 10,000 x 100
The most straightforward way to solve 10,000 x 100 is through direct multiplication:
10,000 x 100
00000 000000 1000000
1,000,000
Therefore, 10,000 x 100 = 1,000,000 (one million).
However, this seemingly simple calculation provides a springboard to explore more sophisticated mathematical concepts.
II. The Power of Place Value
The solution highlights the crucial role of place value in the decimal system. Each digit in a number holds a specific value based on its position. In 10,000, the 1 represents ten thousand, while in 100, the 1 represents one hundred. When we multiply these numbers, we are essentially combining these place values. Understanding place value is fundamental to arithmetic operations, especially with larger numbers.
III. Multiplication as Repeated Addition
Multiplication can be understood as repeated addition. 10,000 x 100 is equivalent to adding 10,000 one hundred times: 10,000 + 10,000 + 10,000 + ... + 10,000 (100 times). While this method is impractical for large numbers, it provides a conceptual link between addition and multiplication, illustrating the fundamental nature of multiplication as a shortcut for repeated addition.
IV. Exponential Notation and Scientific Notation
The problem can be expressed using exponential notation:
10,000 = 10<sup>4</sup> 100 = 10<sup>2</sup>
Therefore, 10,000 x 100 = 10<sup>4</sup> x 10<sup>2</sup> = 10<sup>(4+2)</sup> = 10<sup>6</sup> = 1,000,000.
This demonstrates the rule of exponents: when multiplying numbers with the same base, we add the exponents. This method is particularly useful when dealing with very large or very small numbers, providing a concise and efficient way to represent them. Using scientific notation, we can represent 1,000,000 as 1.0 x 10<sup>6</sup>. This notation is essential in scientific and engineering applications where dealing with extremely large or small quantities is commonplace.
V. Scaling and Real-World Applications
The multiplication 10,000 x 100 demonstrates the concept of scaling. Imagine a square with sides of 100 units. Its area is 100 x 100 = 10,000 square units. Now, imagine scaling up this square by a factor of 100. Each side now measures 10,000 units, and the area becomes 10,000 x 10,000 = 100,000,000 square units. This illustrates how scaling affects area (and volume in three dimensions).
This concept has far-reaching implications:
- Business and Finance: Scaling up production, investments, or marketing campaigns often involves multiplying resources by a certain factor. Understanding scaling helps in predicting the outcomes of such expansions.
- Engineering and Architecture: Scaling is crucial in designing structures, where dimensions need to be adjusted proportionally to maintain structural integrity and functionality.
- Computer Science: Scaling algorithms and data structures is essential for handling increasing amounts of data and ensuring efficient program performance. The ability to scale efficiently is a critical consideration in software design.
- Environmental Science: Scaling factors are used in environmental modelling to extrapolate data from smaller samples to larger populations or regions, allowing for broader analyses of environmental phenomena.
VI. Exploring Related Mathematical Concepts
The calculation 10,000 x 100 opens doors to several related mathematical concepts:
- Factors and Multiples: 10,000 and 100 are multiples of 10. Understanding factors and multiples is crucial for simplifying calculations and solving problems involving divisibility.
- Prime Factorization: Both 10,000 and 100 can be expressed as products of prime numbers (2 and 5). Prime factorization is a fundamental concept in number theory with applications in cryptography and other advanced mathematical fields.
- Arithmetic Progressions and Geometric Progressions: While not directly involved in this specific calculation, understanding arithmetic and geometric progressions is crucial for solving problems involving sequences and series, which have applications in various fields, including finance and physics.
VII. Beyond the Numbers: The Importance of Conceptual Understanding
While obtaining the correct answer (1,000,000) is important, the true value lies in understanding the underlying mathematical principles. This involves grasping the significance of place value, the relationship between multiplication and addition, the power of exponential notation, and the concept of scaling. This deeper understanding is far more valuable than simply memorizing the multiplication table. It empowers individuals to solve a wider range of problems and fosters a more intuitive grasp of mathematics.
VIII. Frequently Asked Questions (FAQ)
Q1: Are there other ways to solve 10,000 x 100 besides direct multiplication?
A1: Yes, as discussed above, you can use exponential notation, repeated addition (though less practical for large numbers), or break down the numbers into smaller, easier-to-manage components and then recombine the results.
Q2: What is the significance of zeros in this multiplication?
A2: The zeros highlight the power of place value. Each zero represents a power of 10. When multiplying by 100 (10<sup>2</sup>), we are essentially shifting the digits of 10,000 two places to the left, adding two zeros.
Q3: How does this calculation relate to other areas of mathematics?
A3: This calculation provides a foundation for understanding more advanced concepts like exponents, logarithms, and even calculus, where understanding the manipulation of very large and very small numbers is essential.
Q4: What are some real-world examples where this type of calculation is used?
A4: Real-world applications are numerous, including calculating areas and volumes, determining financial projections, and scaling up production processes in manufacturing and engineering.
Q5: Why is it important to understand the underlying concepts rather than just memorizing the answer?
A5: Understanding the underlying concepts allows for flexibility and problem-solving in diverse situations. Memorizing only the answer limits your ability to adapt to new challenges and restricts your mathematical fluency.
IX. Conclusion: More Than Just Numbers
The seemingly simple multiplication problem of 10,000 x 100 serves as a gateway to a richer understanding of mathematics. By exploring the underlying principles and their applications, we move beyond rote memorization to develop a deeper appreciation for the power and versatility of numerical manipulation. This understanding is not just beneficial for academic pursuits but also crucial for navigating the complexities of the modern world, where quantitative reasoning is increasingly vital across various disciplines and professions. The answer, 1,000,000, is just the beginning of a much larger and more fascinating mathematical journey.
Latest Posts
Latest Posts
-
45mph To Kmh
Sep 16, 2025
-
Spanish For Clock
Sep 16, 2025
-
Hazel Bryan Massery
Sep 16, 2025
-
10 Of 320
Sep 16, 2025
-
Pawfection Dog Grooming
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 10000 X 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.